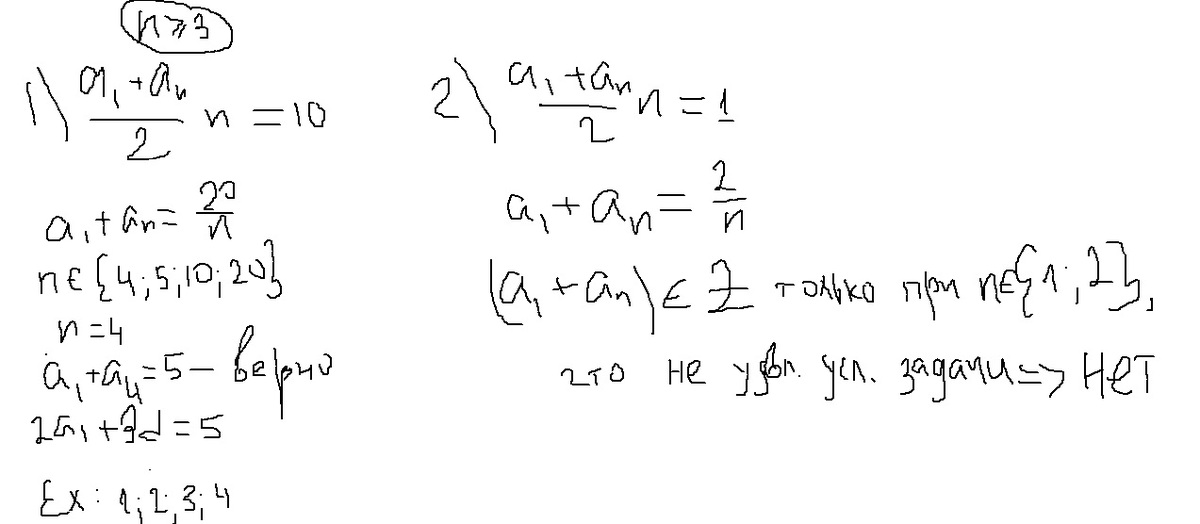прогрессия »
член арифметической прогрессии равен - страница 6
Рассматриваются конечные арифметические прогрессии, состоящие из целых чисел и имеющие не менее трёх членов.
а) Может ли сумма членов такой прогрессии быть равной 10?
б) Может ли сумма членов такой прогрессии быть равной 1?
Решение: Раз каждый член арифм. прогрессии есть число целое, то, как следствие, и разность прогрессии, и сумма, есть число целое, остальное на рисунке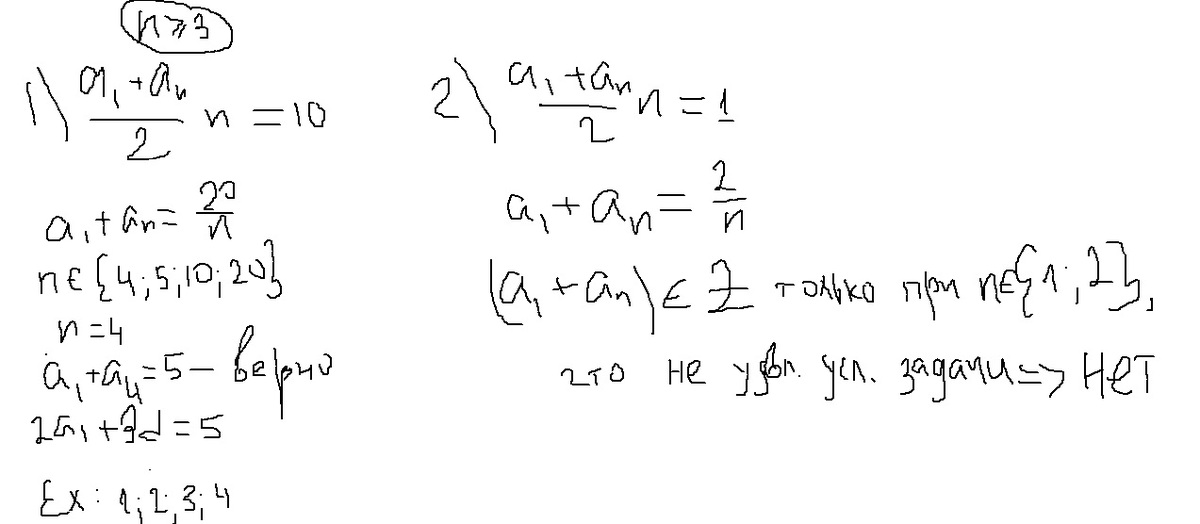
В городе, где жил математик, произошло небольшое землетрясение и циферблат настенных часов в доме математика раскололся на три части. Математик заметил, что суммы чисел,
оказавшихся в разных частях циферблата, образуют арифметическую прогрессию, а сумма всех членов
этой прогрессии равна 60. Как раскололся циферблат?
Решение: Сумма чисел на циферблате равна 78:1+2+3+4+5+6+7+8+9+10+11+12=78
Сумма всех членов арифм. прогрессии на разных частях циферблата - 60, значит,
на одной части числа не составляют прогрессию и их сумма 18:
78-60=18
В эту сумму входят числа:
12+1+2+3
Поэтому может быть 5 вариантов трех "осколков":
12+1+2+3; (4+5) + (6+7+8+9+10+11)=60
12+1+2+3; (4+5+6) + (7+8+9+10+11)=60
12+1+2+3; (4+5+6+7) + (8+9+10+11)=60
12+1+2+3; (4+5+6+7+8) + (9+10+11)=60
12+1+2+3; (4+5+6+7+8+9) + (10+11)=60