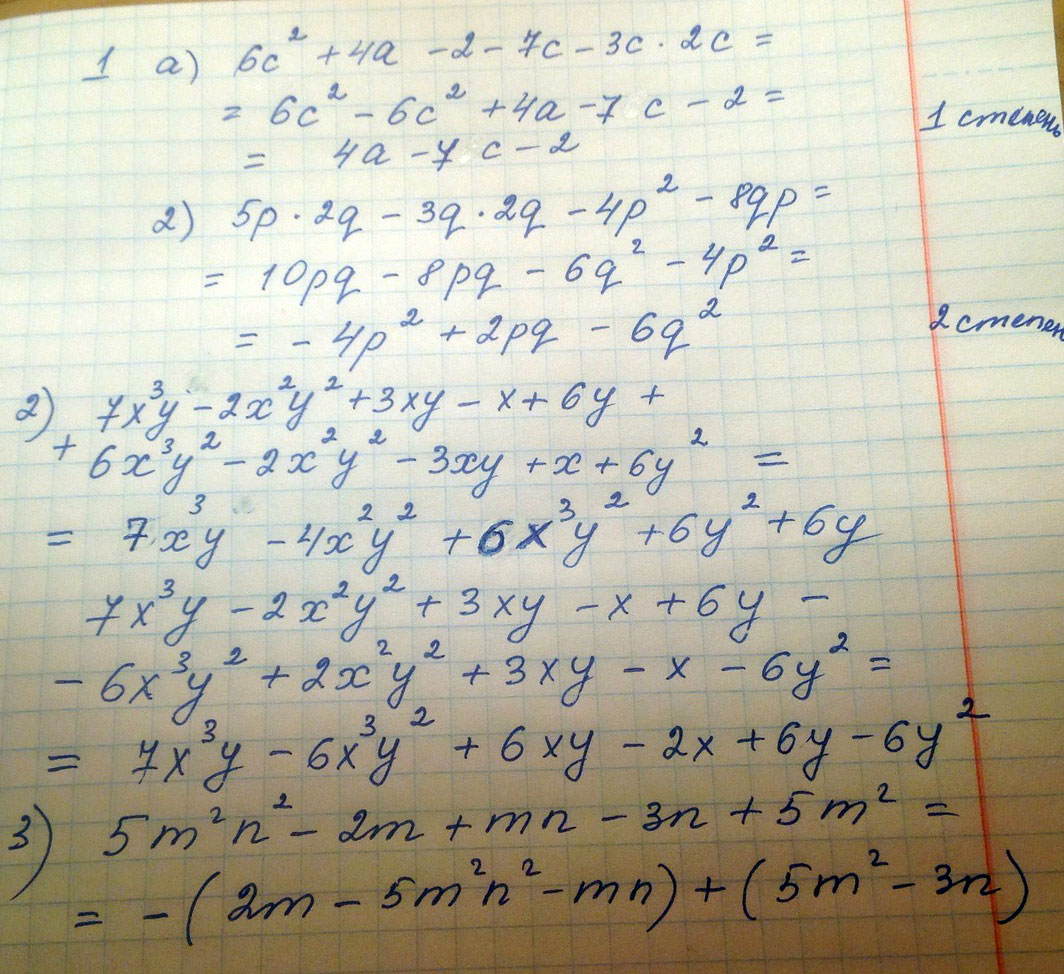прогрессия »
найдите сумму первых членов геометрической прогрессии
1) Чем суммы похожи? Чем различаются?7 км 86 м + 2 км 59 м
7 м 86 см + 2 м 59 см
2) Найди значения сумм и сравни их между собой. Почему при выполнении действий с одинаковыми числами получились разные результаты?
3) Подумай, какие единицы измерения массы нужно использовать, чтобы сумма
7 ... 86... + 2... 59...
дала числовой результат, равный значению первой суммы из пункта 1. Какие единицы измерения массы позволят получить результат, равный результату второй суммы?
4) Запиши три суммы, похожие на первую из данных в пункте 1, и столько же - на вторую.
Решение: 7 км 86 м+2 км 59 м= 9 км 145 м=
2) 7 м 86 см+2 м 59см= 9 м 145см.=10м 45 см.
1) Суммы похожи числовыми значениями, но различаются мерами длин.
2) Получились разные результаты, так как км=1000 м, а м=100см.
3) 1 кг=100 г, следовательно, 7 кг 86 г+2 кг 59 г= 9 кг 145 г.
1 центнер=100 кг, поэтому 1 ц 86 кг+2 ц 59 кг= 10 ц 45 кг.
4)a) 1 тонна = 1000 кг. 7 тонн 86 кг+2 тонны 59 кг= 9 тонн 145 кг.
1 м=1000 мм. 7 м 86 мм+2 м 59 мм= 9 м 145 мм.
1 г=1000 мг. 7 г 86 мг+2 г 59 мг=9 г 145 мг.
b) 1дм=100мм. 7 дм 86 см+ 2 дм 59 мм= 10 дм 45 мм.
1 кв.метр=100 кв.дм. 7кв.м 86кв.дм+2кв.м 59 кв.дм= 10 кв.м 45 кв.дм.
1 кв.дм=100 кв.см. 7кв.дм 86 кв. см+2 кв.дм 59 кв.см= 10 кв.дм 45 кв. см.Составь выражения и найди их значения. Найти 60% площади прямоугольника со сторонами 16 см и 50 см Во сколько раз 5/8 от 96 больше чем 5/13 от 78 2) одна сторона треугольника равна 8 (целых ) 1/5 см вторая на 1 ( целую) 4/5 см меньше первой а сумма этих сторон на 3( целых) 4/5 см больше третьей стороны чему равен периметр треугольника 3) напиши формулы описывающие движение объектов в первых двух задачах
Решение: 1) 50*16*60/100=480 - 60 процентов площади прям-ка96*5/8=60 78*5/13=30 60/30=2 в два раза
2) 8(ц) 1/5 см= 8,2см
1(ц) 4/5см= 1,8 см
3(ц) 4/5см=3,8 см
8,2-1,8=6,4 см - вторая сторона
( 6,4+8,2) - 3,8=10,8 см - третья сторона
8,2+6,4+10,8=25,4 см - периметр треугольника
1) Запиши многочлен в стандартном виде и найдите его степень:
а) 6c² + 4a - 2 - 7c - 3c * 2c
б) 5p * 2q - 3q * 2q - 4p² - 8qp
2)Найдите сумму и разность многочленов:
7x³y - 2x²y² + 3xy - x + 6y И 6x³ y² - 2x²y² - 3xy + x + 6y²
3)Заключите первые три члена многочлена в скобки со знаком - перед ними, а последние два - в скобки со знаком + перед ними:
5m²n² - 2mn + mn - 3n + 5m²
Решение: 1)
а) =6c² -6c²+4a-2-7c=4a-7c-2 (степень 1)
б) =10pq -6q²-4p²-8pq=-6q²-4p²+2pq (степень 2)
2)
7x³y-2x²y²+3xy-x+6y + 6x³y²-2x²y²-3xy+x+6y² =
=7x³y +6x³y²-4x²y²+6y²+6y
7x³y - 2x²y² + 3xy - x + 6y - (6x³ y² - 2x²y² - 3xy + x + 6y²)=
= 7x³y - 2x²y² + 3xy - x + 6y - 6x³ y² + 2x²y² + 3xy - x - 6y² =
= 7x³y -6x³y²+6xy -2x -6y²+6y
3) = - (-5m²n² + 2mn -mn) + (5m² - 3n)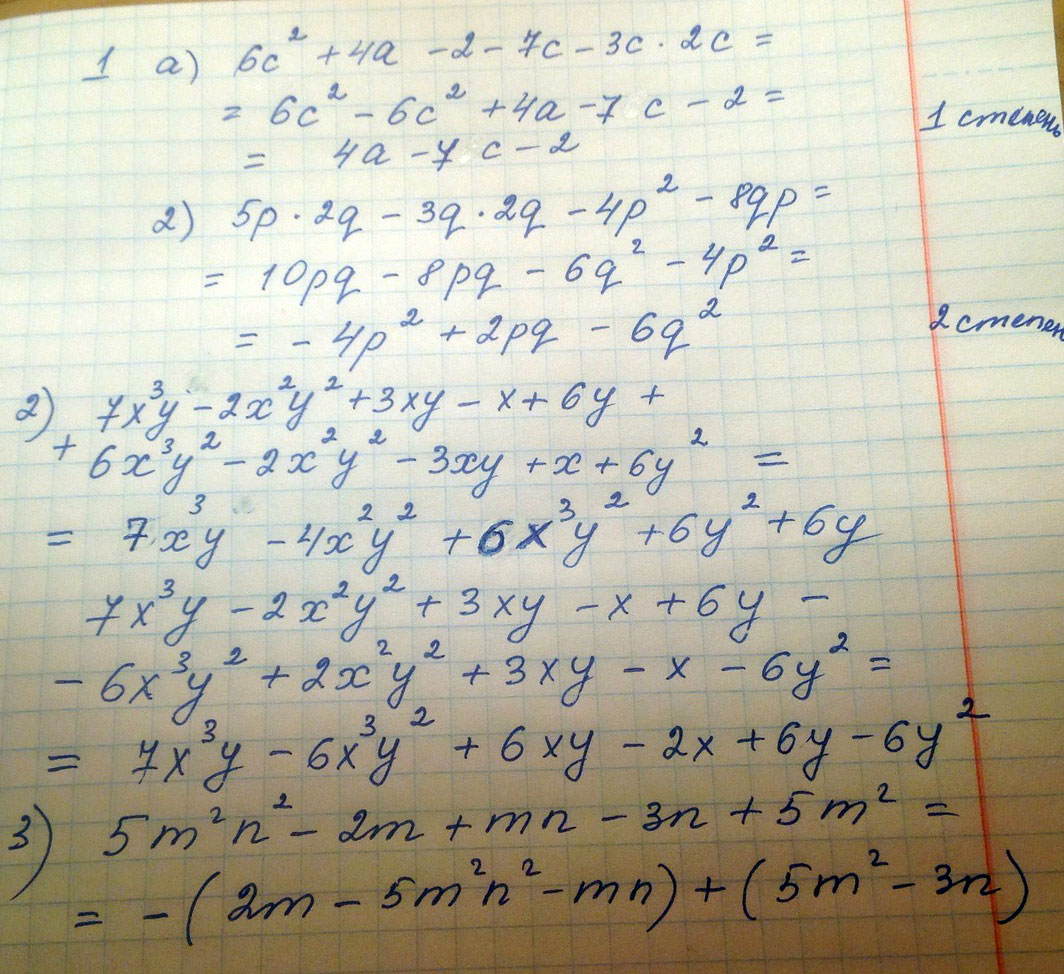
Чётная степень числа x равняется четырёхзначному числу, первая цифра которого равняется 3, а последняя - 5. Найдите число x. Назовите сумму его цифр.
Решение: Так как при возведении х(икс) дает последнюю цифру 5 то и последняя цифра х(икса) 5
Если предположить что стпень возведения 2 (два)
То значение х(икс) должно находиться меду
√3995≈63.2
и √3005≈54.8
Едиственное число с последней цифрой 5(пять)
это 55 дает 55²=3025 Подходит
Если степень 4 (четыре)
то значение должно находится между
3995^(1/4)≈7,95
3005^(1/4)≈7,4
Нужного значения нет, и даже 5^4=625 не подходит.
Аноглогично 5^6=15625 перебор.
Единственный ответ х=55 и 5+5=10Найдите знаменатель геометрической прогрессии если сумма первого и четвертого равна 35 а сумма второго и третьего равна 30, известно что прогрессия возрастающая
Решение: По условию
b₁+b₄=35
b₂+b₃=30
Имеем систему двух уравнений:
b₁+b₁q³=35 ⇒b₁(1+q³)=35 ⇒ b₁=35/(1+q³) и подставим во второе:
b₁q+b₁q²=30 ⇒b₁q(1+q)=30
35q(1+q)/(1+q³)=30
7q/(1-q+q²)=6
7q=6-6q+6q²
6q² - 13 q +6=0
D=169-4·6·6=25
q=(13-5)/12<1 не удовл условию q=(13+5)/12=1,5
Ответ. q=1,5