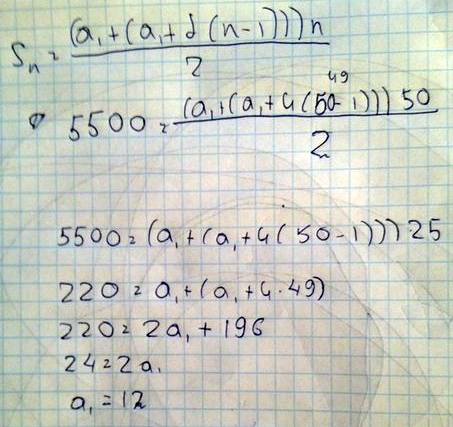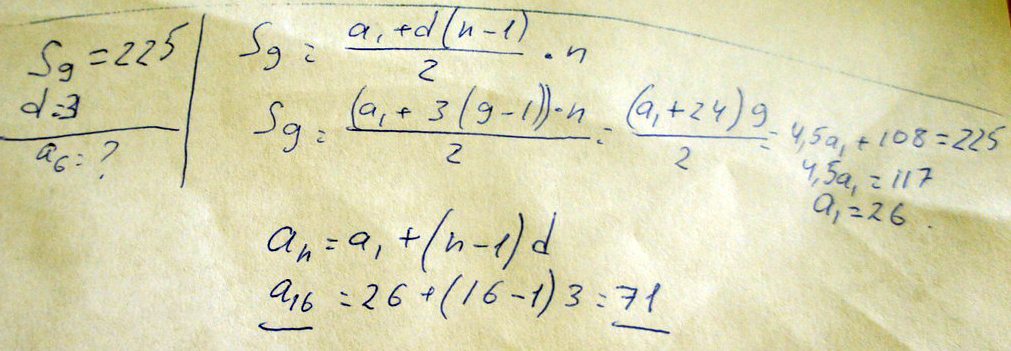найдите сумму первых членов геометрической прогрессии - страница 3
найдите первый член арефметичнои прогрессии, разность которой равна 4, а сумма первых пятидесяти членов равна 5500.
Решение: Вам просто надо запомнить формулу! Sn= ((a1+an)n)/2
не знаю как сделать уравнение в новом оформлении сайта. короче. an(n тут индекс) а где после скобки n стоит, там умножить на nS_50 = (2a_1 +49d)*50/2 = (2a_1 + 49*4)*25
5500 = 50a_1 + 4900
50a_1 = 5500 - 4900
50a_1 = 600
a_1 = 600/50
a_1 = 12
Ответ. 12
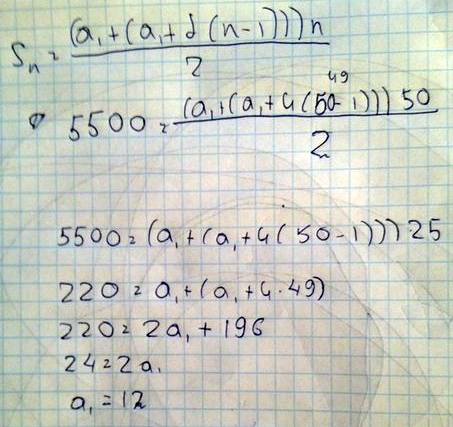
2. Сумма второго, четвертого и шестого членов возрастающей арифмет. прогрессии равна 33, а их произведение равно 935. Найдите произведение первого члена на разность прогрессии.
3. Найдите сумму целых решений неравенства |2х+1/х-3| больше либо равно 1
Решение: 2. Пусть а - второй член прогрессии, d - разность.
Тогда четвертый член = а + 2*d
Шестой = a + 4*d
Имеем систему уравнений:
a + a + 2d + a + 4d = 33
a(a+2d)(a+4d) = 935
3a + 6d = 33 => a + 2d = 11 - четвертый член прогрессии
11a(a+4d) = 935
a(a+4d) = 85
a + 4d = a + 2d + 2d = 11 + 2d
a = a + 2d - 2d = 11 - 2d
a(a+4d) = (11+2d)(11-2d) = 121 - 4d^2 = 85
4d^2 = 36
d^2 = 9
d = 3 и d = -3
Но т. к. прогрессия возрастает, то d = -3 не подходит
a + 2d = 11 => a = 11 - 2d = 5
а - второй член прогрессии
Первый найдем так: a - d = 5 - 3 = 2
В ответе надо найти произведение первого члена и разности: 2 * 3 = 6
Дана арефметическая прогрессия сумма её первых девети челенов равна 225 найдите шестнадцатый челен прогрессии
если разность равна 3
Решение: Сумма первых девяти членов: S= (a1+a(n))*n/2 = (a1 + a9) * 9/2 =225, так как n=9
Значит, a1+a9 = 225*2/9 = 450/9 = 50
разность d равна 3, следовательно: а9 = a1 + (9-1) * d= a1 + 8*3=a1+24
тогда a1+a1+24=50
2*a1 = 26
a1=13
тогда a16 = a1 + (16-1)*d = 13 + 15 *3 = 45+13 = 58шестнадцатый челен прогрессии- 71
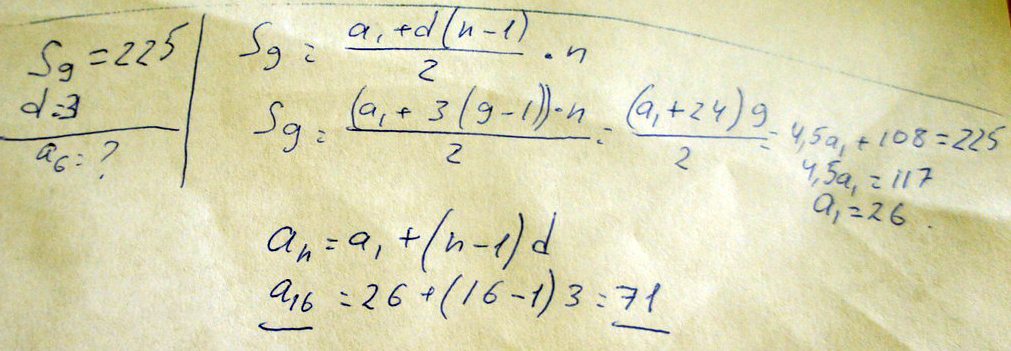
Дана прогрессия 5,10, 20,40, Сумма первых ее n членов равна -425. Найдите число n.
Решение: Sn = (2*a1+(n-1)*d)*n) / 2a1 - первый член прогрессии (у нас это 5)
d - разность прогрессии
n - количество членов, для которых мы считаем сумму.
Итак, поехали. Сначала найдем d. Для этого нужно поделить соседние члены прогрессии.
d = -10 / 5 = -2
Теперь подставляем известные нам данные в формулу, посчитаем что сможем и выразим n.
-425 = ((2*5+(n-1)*(-2))*n)/2
-425 = (10 + (-2*n+2)*n)/2
-425 = (10 -2*n^2 + 2*n)/2
- 2n^2 + 2n + 10 = -850
-2n^2+2n+10+850=0
-2n^2+2n+860 = 0
Вот и получилось у нас квадратное уравнение ;)
разделю его на - 2, чтобы проще было решать.
n^2-n-430 = 0
Теперь считаем дискриминант
D= b^2 - 4ac
a - коэффициент перед х в квадрате
b - коэффициент перед х
с - число без переменной.
D= 1 + 4*430= 1721
n = (-b2+-корень из D)/2
n1 = (1+корень из 1721)/2
n2 = (1- корень из 1721)/2
Потом в итоге получется 2 разных n. В ответ пиши только положительное, т. к. отрицательных n не бывает.
Дана прогрессия 5,10, 20,40, Сумма первых ее n членов равна -425. Найдите число n
Решение: $$ b_{2}=b_{1}q; q=\frac{b_{2}}{b_{1}}=-2 $$$$ S_{n}=\frac{b_{1}(q^n-1)}{q-1} $$
$$ \frac{5((-2)^n-1)}{-2-1}=-425 $$
$$ \frac{(-2)^n-1}{-1}=-85 $$
$$ (-2)^n=85*3+1=256=2^8=(-2)^8 $$
n=8
$$ b_1=5;b_2=-10;b_3=20;b_4=-40 $$
Знаменатель прогрессии равен
$$ q=\frac{b_2}{b_1}=\frac{-10}{5}=-2 $$
Используя формулу суммы членов геометрической прогрессии найдем число n:
$$ S_n=b_1*\frac{q^n-1}{q-1};\\\\5*\frac{(-2)^n-1}{-2-1}=-425;\\\\(-2)^n-1=-425:5*(-3);\\\\(-2)^n-1=255;\\\\ (-2)^n=255+1;\\\\(-2)^n=256;\\\\(-2)^n=(-2)^8;\\\=8 $$
ответ: 8