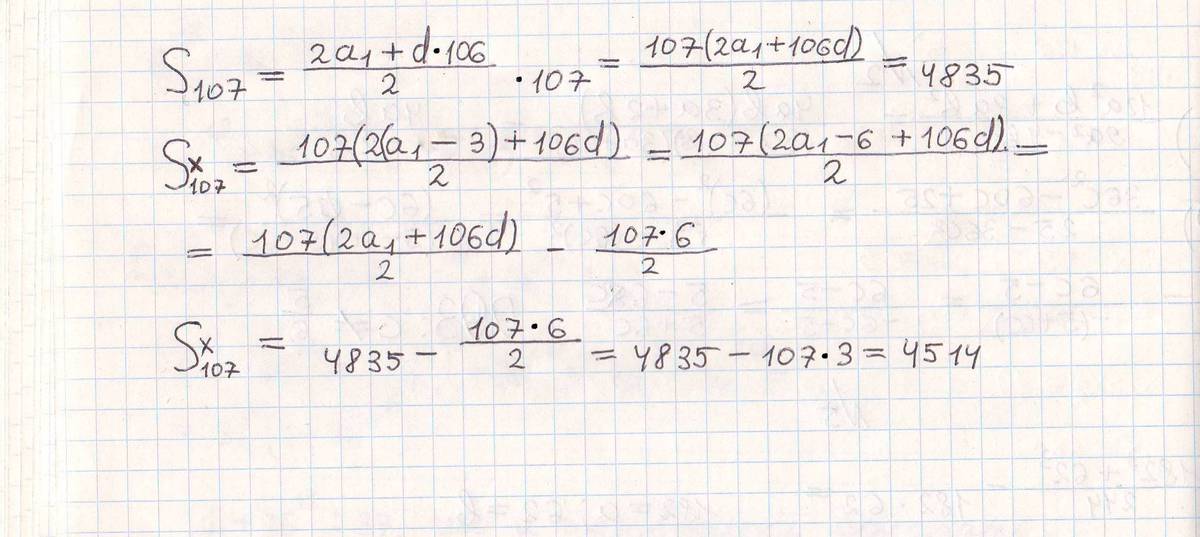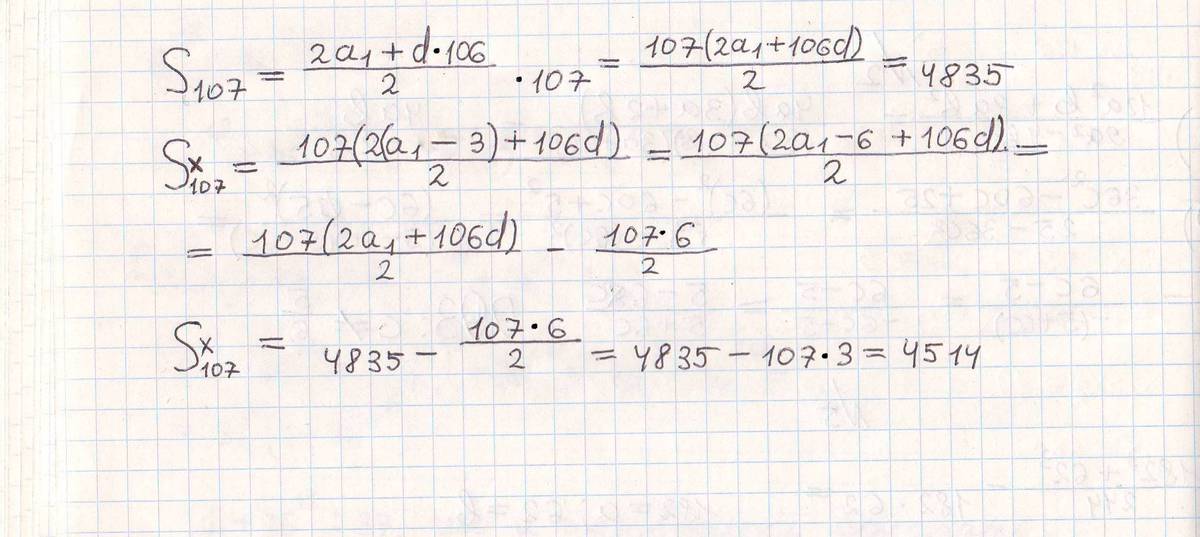прогрессия »
найдите сумму первых членов геометрической прогрессии - страница 5
дана арефметическая прогрессия -7,9,11. найдите сумму первых семи членов этой прогрессии
Решение: арифм. прогрессияa1=3; a2=7; a3=11;a4=15.
d=4
по формуле суммы первых n-членов арифмюпрогрессии
S=((2*a1+(n-1)*d)/2)*n=((2*3+(5-1)*4)/2)*5=55
n=5, т. к. надо найти сумму первых пяти членов
______________________________________________________а1=3 а2=7 значит d=4, потом по формуле Аn=а1+d(n-1)
Аn=3+4(10-1)=3+36=39
S10= а1+An/2*n= 3+ 39/2*10=210
Найдите три числа, являющиеся первыми тремя членами гометрической прогрессии, у которой сумма первого и третьего члена равна 52, а квадрат второго члена равен 100.
Решение: Пусть x- первый член геометрической прогрессии. второй член геометрической прогрессии x*y, третий член геометрической прогрессии x*y*y.
составим систему уравнений:
x+x*y*y=52
(x*y)^2=100.
только одно число в квадрате дает 100, т. о. второй член геометрической прогрессии равен 10.
x*y=10
10/y=52/(1+10*y)
10+100y=52y
48y=-10
y=-5/24.
первый член геометрической прогрессии равен
10/(-5/24)=-48.
третий член геометрической прогрессии равен
10*(-5/24)=-25/12
ответ:-48,10,25/12Сумма первого и пятого членов прогрессии равна -2, а сумма второго и шестого её членов равна 2. Найдите сумму первых десяти членов прогрессии.
Решение: $$ x_{n} = x_{1} + d*(n-1) $$
$$ x_{1} + x_{5} =-2 $$
$$ x_{2} + x_{6} =2 $$
-2=x(1)*2+d*4
2=x(1)*2+d*5
x(1)=(-2+d*4)/2
x(1)=(2-d*5)/2
-2-d*4=2-d*5
d=4
x(1)=(-2+4*4)/2=7
x(10)=7+4*9=43Воспользуюсь частью предыдущего ответа:
-2=x(1)*2+d*4
дальше правлиьно будет так:
2=x(1)*2+d*6
отнимем от второго уравнения первое (левую часть от левой, правую от правой)
2 - (-2) = 2*x1 +d*6 - (2*x1+d*4)
4 = 2*d
d = 2.
2=x(1)*2+d*6
x1 = (2 - 2 * 6)/2 = -10/2 = -5
x10 = -5 + 2 * 9 = 13
S = (x1 + x10) / 2 * 10 = (13 - 5) * 5 = 40
Сумма квадратов первого и третьего членов геом. прогрессии равна 257. Найдите сумму n первых членов прогрессии, если известно, что отношение суммы второго, третьего и пятого членов прогрессии к сумме третьего, четвёртого и шестого её членов равна 4.
Решение: Если известно, что отношение суммы второго, третьего и пятого членов прогрессии к сумме третьего, четвёртого и шестого её членов равна 4, то:
$$ \frac{aq+aq^2+aq^4}{aq^2+aq^3+aq^5} =4 \\ \frac{aq(1+q+q^3)}{aq^2(1+q+q^3)} =4 $$
1/q = 4 q = 1/4
Сумма квадратов первого и третьего членов геометрической прогрессии равна 257.
Тогда а² + (aq²)² = 257 а² + a²q⁴ = 257 a²(1+q⁴) = 257 a² = 257/(1+q⁴)
a² = 257 / 1+(1/4)⁴ = 256 a = 16
Sn= (16-an*1/4) / (1-1/4) =(64-an) / 3.
Сумма первых ста семи членов арифм. прогр. равна 4835. Найдите сумму первых ста семи членов такой прогрессии, каждый член которой на 3 меньше соответствующего члена данной прогрессии.
Решение: $$ S_{107} $$ — сумма первоначальной прогрессии;
$$ S^x_{107} $$ — сумма прогрессии, которую мы ищем.
Ответ: $$ 4514. $$