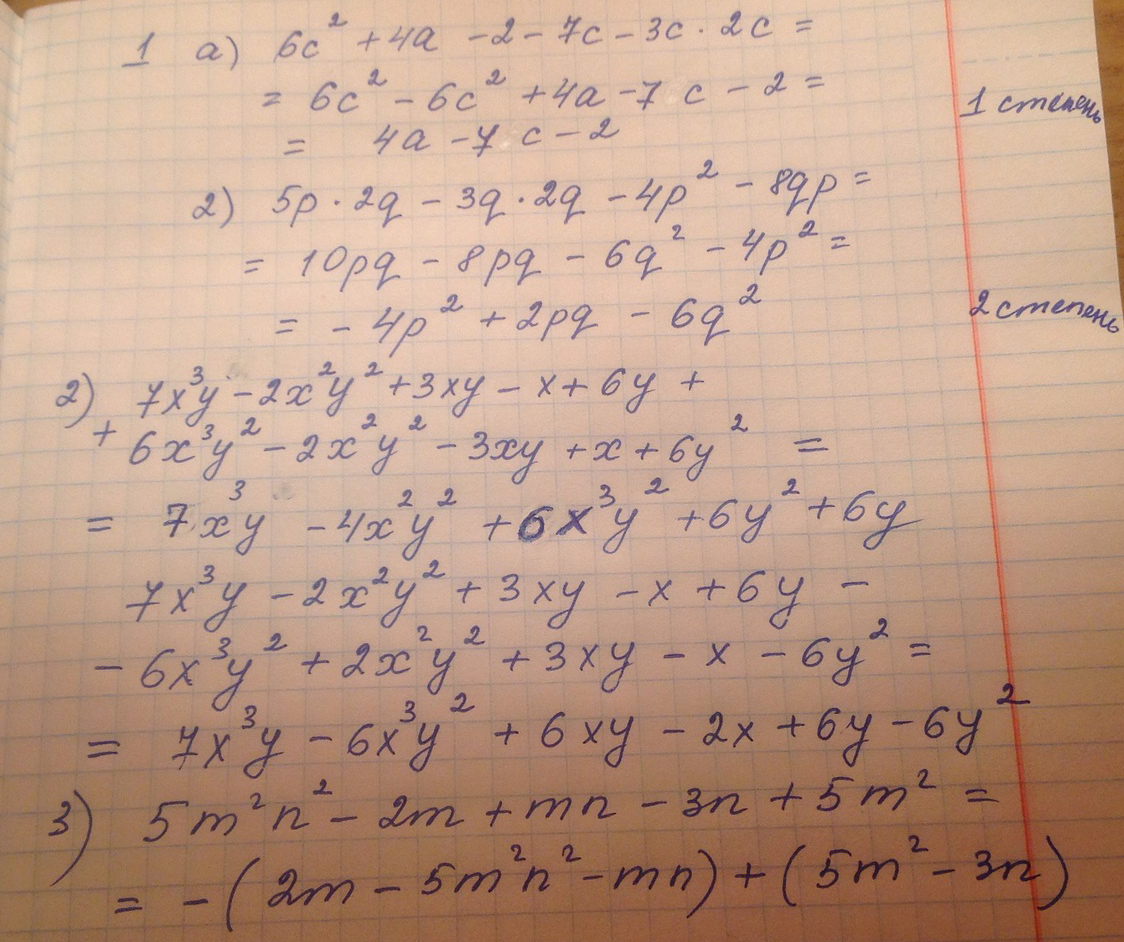найдите сумму первых членов геометрической прогрессии - страница 7

1) В железной руде содержаться железо и прмеси в отношении 7:2. Сколько тонн железа получится из 189 т руды?
2) Масса двух мотров 52 кг. Масса одного из них в две целых пять седьмых больше другого. Найдите массу каждого мотора.
3) Туристы отправились в трёхдневный поход. В первый день прошли- 7/22 всего пути, во второй- 1/3 оставшегося пути, а в третий- последние 25 км. Найдите длину туристского маршрута.
4) Найдите не известное число, если полусумма этого числа и числа 12,3 больше полуразности числа 1,5 и неизвестного числа 3.
5) Решите задачу, выделяя три этапа математического моделирования.
В кабиете математики в трёх шкафах лежат модели геометрических фигур. Во втором шкафу на 4 модели больше, чем в третьем, и на 15 меньше, чем в первом. Сколько моделей в каждом шкафу, если всего в кабинете 50 моделей?
6) Придумайте задачу, матиматическая модель котрая указана ниже, и решите её.
5х+4(х+20)=620
7) Запишите координаты точек, котрые делят отрезок АВ на три равные части, если А(-1), В(8).
8) Найдите координаты точек, отстоящих на расстоянии 4,5 единичных отрезка от точки М(2,3)
9) сумма двух чисел равно 7. Если одно число увеличить в 2 раза, а другое оставить без изменения, то в сумме эти числа дадут 8. Найдите исходные числа.

Решите с помощью систем рациональных уравнений
1. Двое рабочих, работая вместе, выполнили всю работу за 5 дней. Если бы первый рабочий работал в два раза быстреее, а второй в два раза медленнее, то всю работу они выполднили бы за 4 дня. За сколько дней вополнил бы эту работу первый рабочий?
2. Найдите два числа, если отношение суммы этих чисел к их разности равно 8:1 и разность квадратов этих чисел равно 128. Сколько решений имеет задача?

Примем всю работу за 1.
Тогда 5*(Х+У) = 1 - первый вариант, а 4*(2*Х+0,5*У) = 1 - второй вариант, где
Х - количество работы первого рабочего
У - количество работы второго рабочего
Исходя из этого получаем
5*(Х+У) = 4*(2*Х+0,5*У)
5Х+5У = 8Х+2У
5У-2У = 8Х-5Х
3У = 3Х, из чего следует что Х=У ( рабочие работают одинаково)
Тогда
5*(Х+Х) = 1
10Х = 1
Х = 0,1
Соответственно всю работу один рабочий выполнит за 10 дней

2. a+b/a-b=8/1
a²-b²=128
a+b=8a-8b из этого ур-я выражаем b, b=7/9a и подставляем его во второе
a²-b²=128
a²-49/81a²=128
81a²-49a²=128·81
32a²=10368
a²=324
a1=-18, a2=18
b1=7/9·(-18)=-14
b2=7/9·18=14
ответ :(-18,14) или (18,14)
  

1) Запиши многочлен в стандартном виде и найдите его степень:
а) 6c² + 4a - 2 - 7c - 3c * 2c
б) 5p * 2q - 3q * 2q - 4p² - 8qp
2) Найдите сумму и разность многочленов:
7x³y - 2x²y² + 3xy - x + 6y И 6x³ y² - 2x²y² - 3xy + x + 6y²
3) Заключите первые три члена многочлена в скобки со знаком - перед ними, а последние два - в скобки со знаком + перед ними:
5m²n² - 2mn + mn - 3n + 5m²

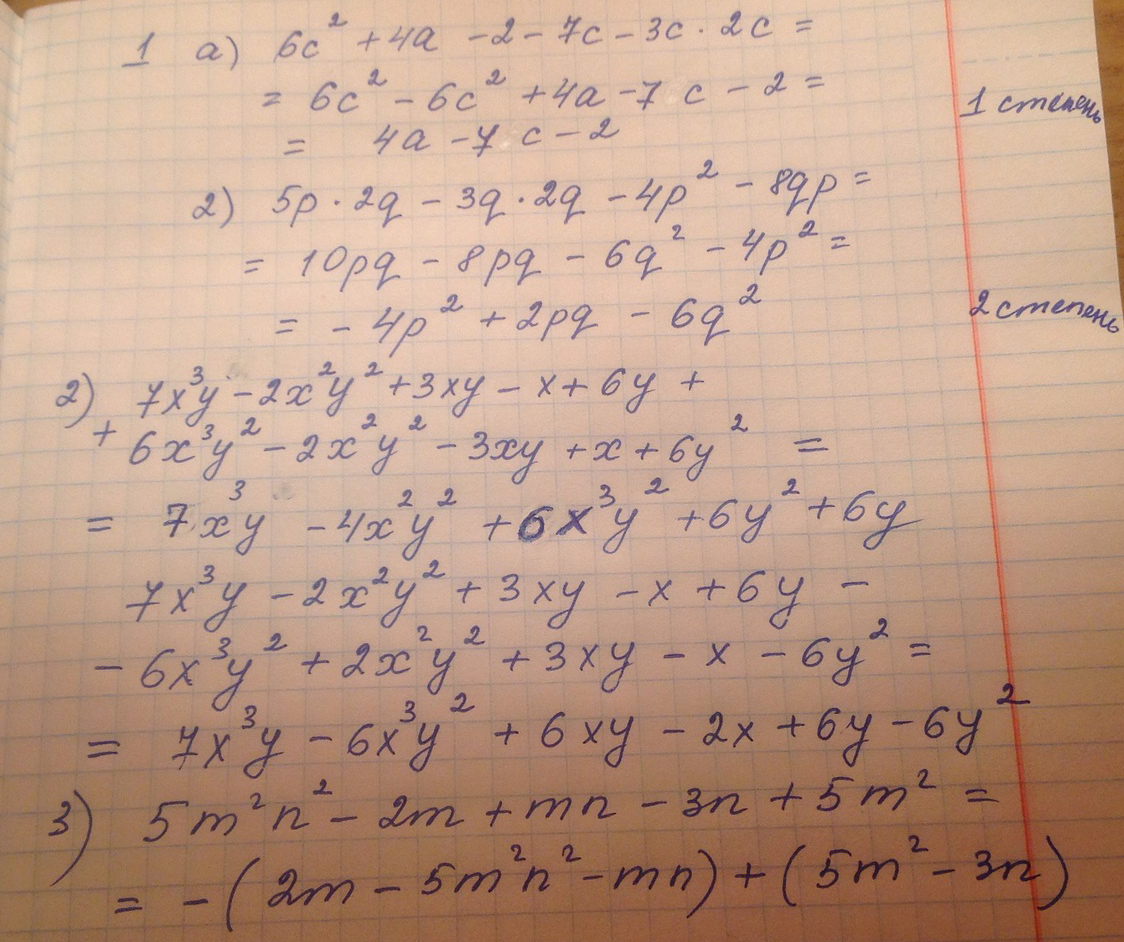
1)
Упростите выражение: 3ху – 3х – (х – 3ху)
2)
Какая из точек А(-10;2), В(2;1), С(3;4) и D(5;-2) принадлежит графику линейного
уравнения 3х- 2у-4=0
3)
Представьте выражение (5х-2)2 в виде многочлена
4)
Решите уравнение: 0,4(х-2) =2(4-х)+3,2.
5)
Найдите разность многочленов х3-2ху+у3 и -4ху-х3+у3.
6)
Функция задана формулой у=3х-5. При каком значении аргумента значение функции равно 19?
7)
Основание равнобедренного треугольника на 6 см меньше суммы боковых сторон. Найдите длину основания этого треугольника, если его периметр 32 см.
8)
Два внутренних угла треугольника равны 62º и 105º. Вычислите сумму их внешних углов.
9)
Разложите на множители многочлен 4ху - 4х – 1 + у
10)
Из одного города в другой одновременно отправились два автомобиля, скорости которых равны 50 км/час и 60 км/час соответственно. Вторая машина прибыла в конечный пункт на 1,5 часа раньше первой. Какое расстояние между городами?
11)
Решите уравнение - (3х-1)2 +2·(5+х)·(х-5) +7х2 = 3

2)B)

 3)10x-4

4)0.4(x-2)=2(4-x)+3.2

0.4x-0.8=8-2x+3.2

0.4x+2x=8+3.2+0.8

2.4x=12

x=5

6)19=3x-5

3x-5=19

3x=19+5

3x=24

x=8

7)пусть боковая сторона х, тогда основание x+x-6

x+x+x+x-6=32

4x-6=32

4x=38

x=9.5

(9.5+9.5)-6=13- основание

8)180-62=118

180-105=75

118+75=193

9)4xy-4x-1+y=(4xy-4x)+(y-1)=4x(y-1)+(y-1)=(y-1)(4x+1)

, решить
Для линейного оператора f известно, что f 5 11 и f 4 = -16
4 = 25 -3 -11. Найдите матрицу этого оператора. В ответе укажите сумму элементов матрицы
2. Известно, что в некотором ортонормированном базисе f
х1 х1+7х2+8х3
х2 =-5х1-х2+8х3
х3 -2х1-4х2+х3. Найдите матрицу оператора f* сопряженного для f. В ответе укажите сумму 3-й строки.
3. Найдите собственные значения и собственные векторы линейного оператора f, если известна его матрица в стандартном базисе F= 12 24
-6 38. Первые координаты собственных векторов приравняйте к 1. В ответе укажите сумму их вторых координат.
4. Методом Лангранжа приведите квадратичную форму
q=x12 +4x1x2+4x1x3+29x2^2+38x2x3+17x3^2к нормальному виду. В ответе укажите сумму коэффициентов нормального вида.

α₁₁ α₁₂

α₂₁ α₂₂

Составим соответствующие уравнения после действия этого оператора

5α₁₁+4α₁₂=11

5α₂₁+4α₂₂=25

4α₁₁-3α₁₂=-16

4α₂₁-3α₂₂=-11

Решая систему находим элемениы матрицы

α₁₁=-1 α₁₂=4

α₂₁= 1 α₂₂=5

Ответ: 9

2) Составим матрицу оператора

 1 7 8 

-5 -1 8

-2 -4 1

Транспонируем ее

1 -5 -2

7 -1 -4

8 8 1

Ответ: 17

3) Решим соответствующее характеристическое уравнение

$$ \left[\begin{array}{cc}12-\lambda&24\\-6&38-\lambda\end{array}\right]=\lambda^2-50\lambda+600=0 $$

Для всех собственных значений найдем собственные вектора

$$ \lambda_1=20 $$

-x₁+3x₂=0

x₁=1 x₂=1/3

$$ \lambda_2=30 $$

-3x₁+4x₂=0

x₁=1 x₂=3/4

Ответ: 13/12

4) x₁²+4x₁x₂+4x₁x₃+29x₂²+38x₂x₃+17x₃²=(x₁+2x₂+2x₃)²+(5x₂+3x₃)²+4x₃²=a₁²+a₂²+4a³₂

Ответ: 6