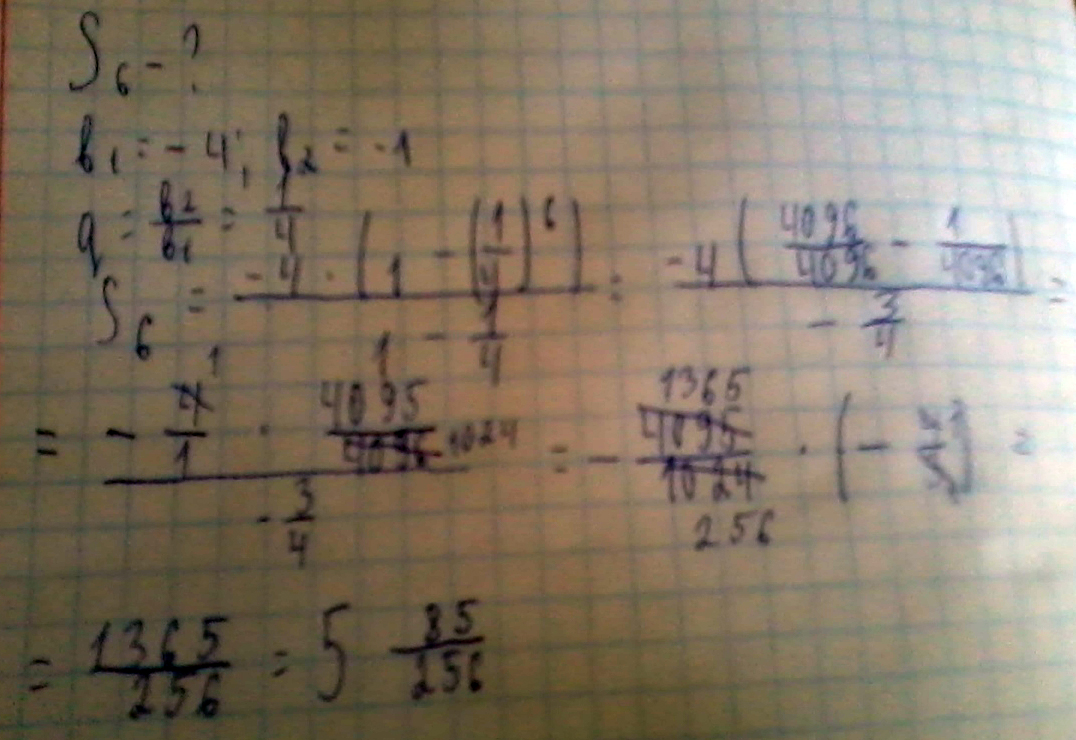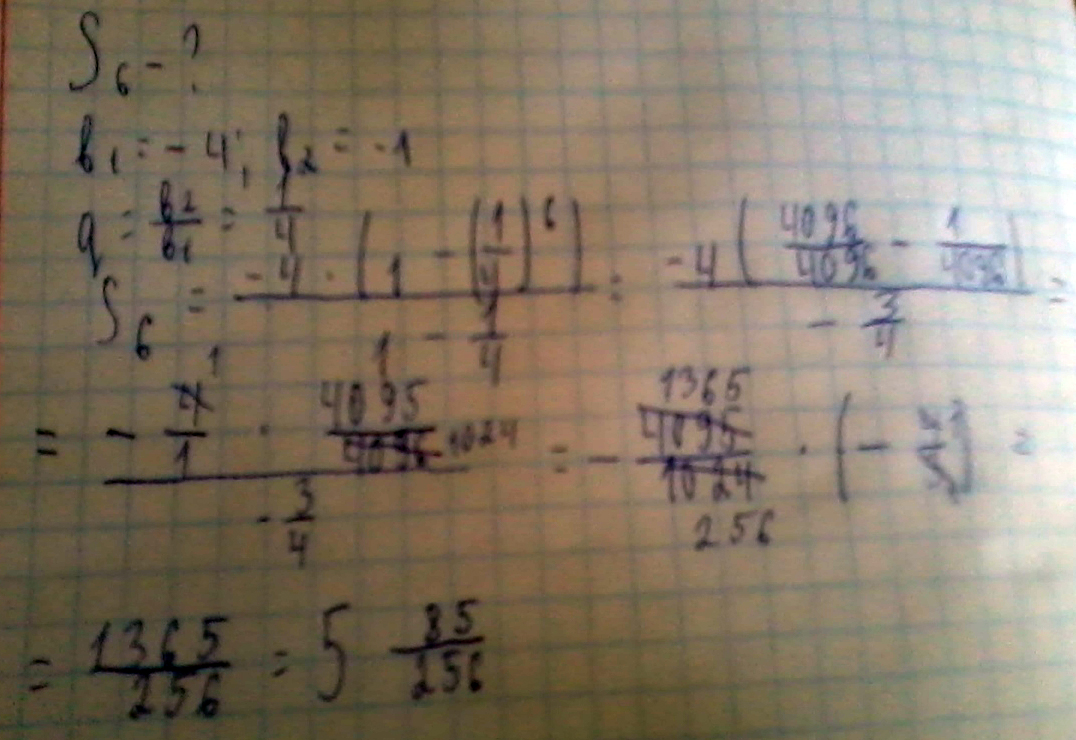прогрессия »

найдите сумму первых членов геометрической прогрессии - страница 4

  • Сумма бесконечно убывающей геометрической прогрессии относиться к сумме двух её первых членов как 4:3. Первый член прогрессии равен 8. Найти сумму квадратов членов этой прогрессии


    Решение: (an)-бесконечно убывающая геометрическая прогрессия

    S(n)=a1/(1-q)

    a1=8

    S(n)=8/(1-q)

    S(2)=a1+a2=8+8q=8(1+q)

    S(n):S(2)=3:4

    8/(1-q) : 8(1+q)=4:3

    1/(1-q^2)=4:3

    q^2=1/4

    q=+-1/2

    ! только при q=1/2 прогрессия будет убывающей

    (an):  8,4,2,1/2,

    S(n1)-сумма квадратов (an)

    S(n1)=b1+b2+b3=8^2+4^2+2^2+.

    q1=b2:b1=4^2/8^2=1/4

    S(n1)=b1/(1-q1)=8^2/(1-1/4)=64/(3/4)=256/3=85 1/3

  • В возростающей геометрической прогрессии b2=6 а сумма первых 3 членов равна 26, найдите разность между первый и третьим членоми этой прогрессии


    Решение: $$ b_{2}=6\\ b_{1}+b_{2}+b_{3}=26\\ b_{1}+b_{3}=20\\ b_{1}(1+q^2)=20\\ b_{1}q=6\\ \frac{1+q^2}{q}=\frac{10}{3}\\ 3+3q^2=10q\\ 3q^2-10q+3=0\\ D=100-4*3*3=8^2\\ q=3\\ q=\frac{1}{3}<1\\ b_{1}=\frac{20}{1+3^2}=2\\ b_{3}=2*3^2=18\\ b_{3}-b_{1}=18-2=16 $$
    Ответ 16 

    """"""""""""""""""""""""""""""""""""""""""""

    b b b b b b b q b q frac q q frac q q q - q D - q q frac lt b frac b b -b - Ответ  ...

  • 1) Между числами 1 и 256 расположите три числа так, чтобы полученные 5 чисел были последовательными членами геометричесской прогрессии. 2) Найдите три числа, являющиеся первыми тремя членами геометричесской прогрессии, у которой, у которой сумма первого и третьего членов равна 52, а квадрат второ


    Решение: 1; х1; х2; х3;256

    Свойство геометрической прогрессии

    х2 в квадрате=1*256

    Отсюда х2=16

    1; х1;16; х3;256

    Свойство геометрической прогрессии

    х1 в квадрате=1*16

    Отсюда х1=4

    Свойство геометрической прогрессии

    х3 в квадрате=16*256

    х3 в квадрате=4096

    Отсюда х3=64

    Ответ: 4;16;64

    х х х Свойство геометрической прогрессии х в квадрате Отсюда х х х Свойство геометрической прогрессии х в квадрате Отсюда х Свойство геометрической прогрессии х в квадрате х...

  • Найдите сумму 10 первых членов возрастающей прогрессии, если третий ее член больше второго на 6, а пятый больше третьего на 36


    Решение: Третий член прогрессии:
    b3=b1*q^2
    второй:
    b2=b1*q
    b3-b1=b1*q^2-b1*q=b1*q(q-1)=6 (1)
    b5=b1*q^4
    b5-b3=b1*q^2(q^2-1)=36 (2)
    поделим 2 на 1
    6=q*(q+1) |q^2-1=(q-1)*(q+1)
    q^2+q-6=0
    q=-3;2 (по теореме Виета)
    т. к сказано что возрастающая, то q>0 т. е=2
    подставив q=2 в первое найдём b1:
    b1*2*(2-1)=6
    b1=3
    тогда по формуле суммы получаем:
    S=b1*(q^n-1)/(q-1)
    n=10
    S=3*(2^9)/1=1536
    Ответ 1536.

  • Дана арифметичекская прогрессия:-4;-1; 2, найдите сумму первых шести её членов


    Решение: a2=a1+d
    d=a2-a1
    d=3
    a6=a1+5d
    a6=-4+15=11
    S6=a1+an/2 *n=-4+11/2*6=21
    формула суммы арифметической прогрессии Sn=(a1+an)n/2где s-сумма, а1-первый член( в данном случае это -4)

    a a dd a -a d a a da - S a an n - формула суммы арифметической прогрессии Sn a an n где s-сумма а -первый член в данном случае это -...
<< < 234 5 6 > >>