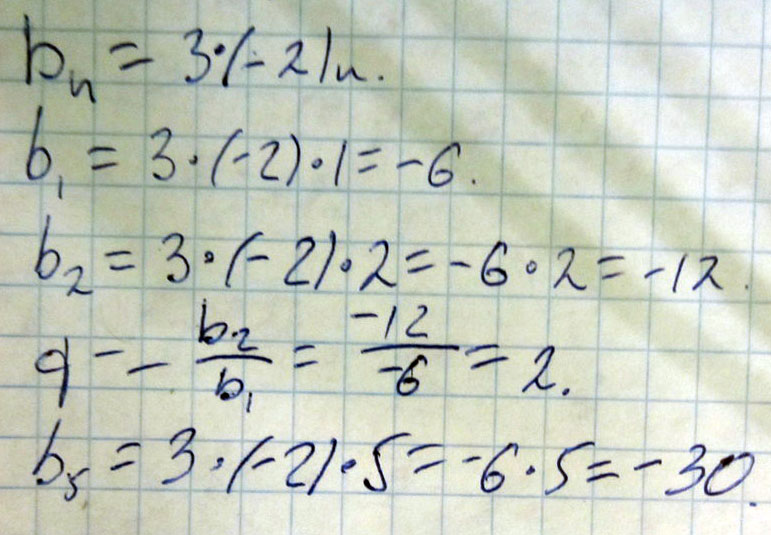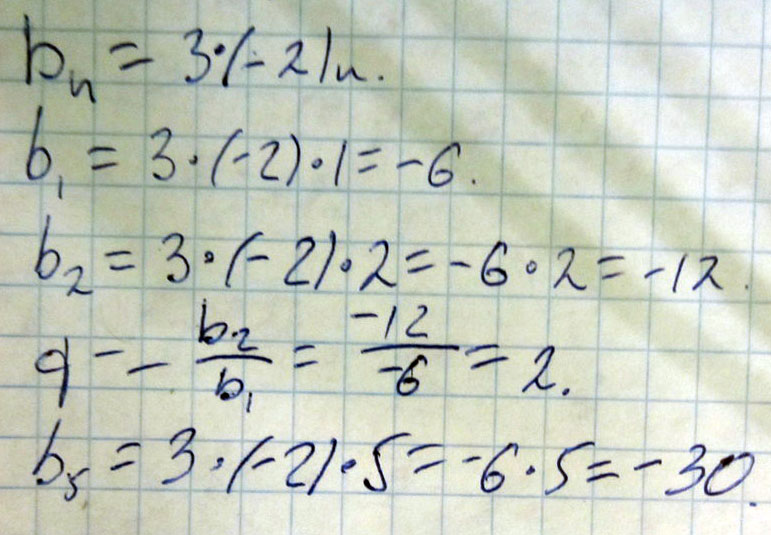прогрессия »

в геометрической прогрессии первый член равен

  • Сумма n первых членов геометрической прогрессии определяется по формуле Sn=3(в степени n) -1. Найти знаменатель прогрессии и ее первыйчлен


    Решение: Sn=(3^n)-1
    n=1
    S1=3-1=2⇒b1=2
    S2=9-1=8
    Sn=b1(q^n-1)/q-1
    2(q^2-1)/q-1=8
    (q^2-1)/q-1=4
    q^2-1=4q-4
    q^2-4q+3=0
    q=1 искл q=3
    ответ b1=2 q=3

    $$ S_n=3^n-1 $$
    В общем виде формула суммы геометрической прогрессии имеет вид
    $$ S_n= \frac{b_1(q^n-1)}{q-1} $$
    Попробуем привести данное выражение к подобной форме
    $$ S_n= \frac{1(3^n-1)}{1}=\frac{2(3^n-1)}{3-1} $$
    Сравнивая с общей формулой, видим, что
    знаменатель q=3;
    первый член b₁=2

  • Рассматривается геометрическая прогрессия, заданная формулой n-го члена: cn=27*(-1/3) в степени n-1 а) Найдите сумму её первых пяти членов б) Найдите суммуеё первых n членов в) Сколько надо сложить последовательных членов этой прогрессии, начиная с первого, чтобы получить сумму, равную 61/3


    Решение:

    В геометрической прогрессия, заданной формулой n-го члена: cn=27*(-1/3) в степени n-1 :
    а    ₁ = 27 q = -1/3.
    б) суммa её первых n членов:
    Sn = (a₁*(q^n - 1)) / (q-1).
    а) сумму её первых пяти членов:
    S₅ = (27*((-1/3)⁵- 1)) / (-1/3-1).= -27,111 / (-4/3) = 20,3333 = 61/3.
    в) надо сложить последовательных членов этой прогрессии, начиная с первого, чтобы получить сумму, равную 61/3 - это число 5 (смотри ответ а).

  • знаменатель геометрической прогрессии равен -0.5, а первый член 64. найдите сумму квадратов первых восьми членов этой прогрессии


    Решение: b₁ = 64² = 4096

    b₂ = (-32)² = 1024

    b₃ = 16² = 256

    b₄ = (-8)² = 64

    b₅ = 4² = 16

    b₆ = (-2)² = 4

    b₇ = 1

    b₈ = (-0,5)²= 0,25

    S₈ = 5461,25

    Более правильное решение:

    Так как каждый член прогрессии нужно возводить в квадрат, знаменательно можно представить как (-0,5)² = 1/4, а первый член как 4096.

    $$ S = \frac{b_{1}*(q^{8}-1)}{q-1} = \frac{4096* (0,25^{8}-1)}{0,25-1}\\ 4096 = 0,25^{-6}\\ S = \frac{0,25^{2}-4096}{-0,75} = 5461,25 $$

  • найти знаменатель геометрической прогрессии, если первый ее член равен 4, а третий равен 108


    Решение: bn = b1 * q^n-1

    b3 = 4 * q^2

    108 = 4*q^2

    27 = q^2

    q = 3 корня из 3 (3*sqrt(3))

    знаменатель геометрической прогрессии - это q

    система уравнений:

    b1=4,         b1=4,            b1=4,         b1=4,         

    b3=108       b1*q²=108     4*q²=108    q²=27

    значит q= ± √27=±3√3   

    √-это корень

    но по характеристическому свойству геом. прогр.

    b2-это положительное число, то

    только q=3√3 удовлетворяет условию

    ответ:q=3√3

  • Найдите знаменатель геометрической прогрессии bn=3*(-2)n, а также ее первый и пятый члены.


    Решение: ответ. 

    b1=-6

    q=2

    b5= -30

    Вместо n подставляете номер члена прогрессии, который вам нужно найти

    ответ.  b - q b - Вместо n подставляете номер члена прогрессии который вам нужно найти...
1 2 3 > >>