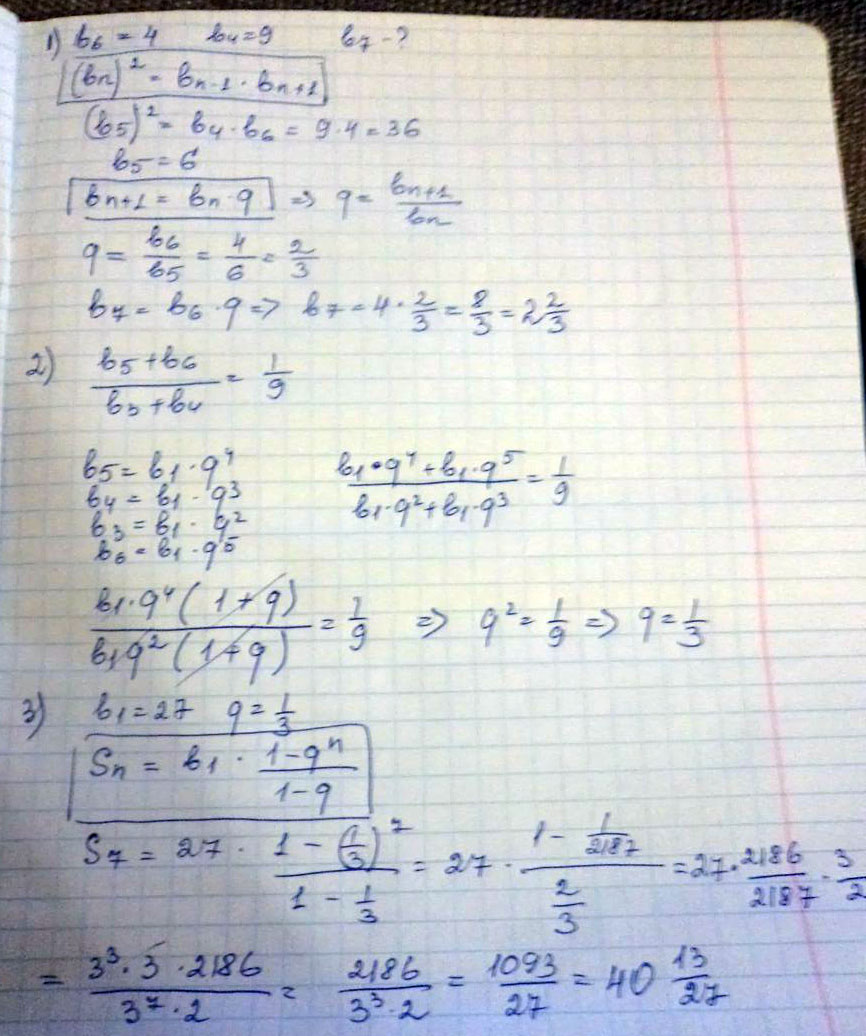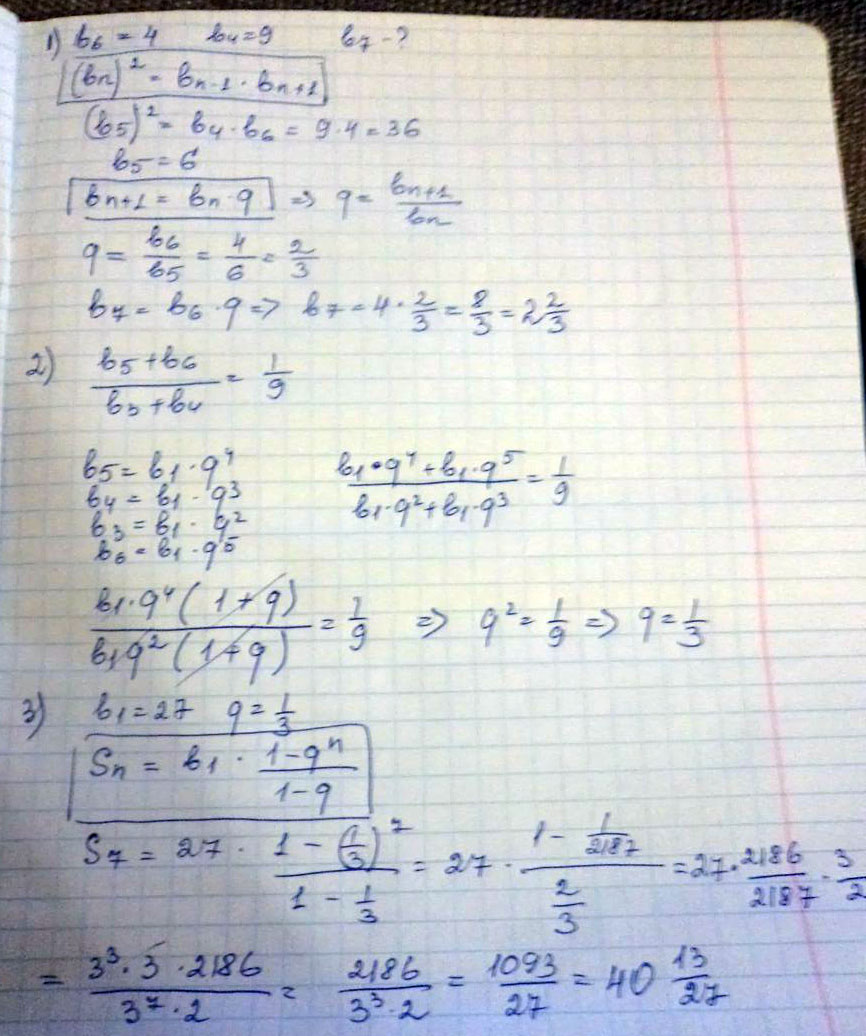в геометрической прогрессии первый член равен - страница 2

Найдите знаменатель геометрической прогрессии, если отношение суммы первых девяти её членов к сумме следующих девяти членов этой же прогрессии равно 512.

Напишем формулу для суммы 9 членов геометрической прогрессии

s9=(b1*(q^9-1))/(q-1)

Напишем формулу для суммы 18 членов геометрической прогрессии

s18=(b1*(q^18-1))/(q-1)

512=2^9

s9/(s18-s9)=2^9

GПеревернем дробь

(s18-s9)/s9=1/2^9

Числитель разделим на знаменатель почленно.

1-s18/s9=1/2^9 Отдельно упростим дробь s18/s9 

s18/s9=(b1*(q18-1)/(q-1))/(b1*(q9-1)/(q-1)

Сократятся b1 и (q-1)

s18/s9=(q18-1)/(q9-1) разность квадратов 

s18/s9=((q:9-1)*(q^9+1))/(q9-1) Сократим на (q^9-1)

s18/s9=q^9+1

Возвращаемся к уравнению

1-s18/s9=1/2^9

1-q^9+1=1/2^9

-q^9=1/2^9

q=-1/2

Найдите первый член а знаменатель геометрической прогрессии, если её четвертый член меньшее шестого на 64, а пятый больше третьего на 192

Знаменатель геометрической прогрессии равен -0.5, а первый член 64. найдите сумму квадратов первых восьми членов этой прогрессии.

b3=-32:(-2)=16

b4=16:(-2)=-8

b5=-8:(-2)=4

b6=4:(-2)=-2

b7=-2:(-2)=1

b8=1:(-2)=-0,5

сумма квадратов=4096+1024+256+64+16+4+1+0,25=5461,25

Заданная последовательность с $$ b_{1}=64 $$ и $$ q=-\frac{1}{2} $$

- геометрическая прогрессия, сумма n первых членов которой вычисляется по известной формуле

$$ S_{n}=\frac{b_{1}\cdot(q^{n}-1)}{q-1} $$

Последовательность, составленная из квадратов членов заданной геометрической прогрессии, предcтавляет собой геометрическую прогрессию:

$$ b_{1}^2, \ q^2b_{1}^2,\ q^4b_{1}^2,\ q^6b_{1}^2,\ $$.$$ b_{1}^{2}\cdot{q}^{2(n-1)} $$, в которой $$ B_{1}=b_{1}^{2}\ $$ и $$ Q_{1}=q^{2}\ $$

Сумма n первых членов такой прогрессии вычисляется по вышеприведённой формуле для Sn. Если подставить в эту формулу $$ B_{1}=b_{1}^{2} $$ и $$ Q=q^2 $$, то получим

$$ S_{n}=\frac{b_{1}^{2}\cdot(q^{2n}-1)}{q^{2}-1} $$

Подставляем сюда $$ b_{1}=64 $$ и $$ q=-\frac{1}{2}$$:

$$ S_{8}^{Q}=\frac{64^{2}\cdot((\frac{-1}{2})^{2\cdot{8}}-1)}{\frac{1}{4}-1}=5461,25 $$

В геометрической прогрессии (an) a1=2, а произведение первых четырех ее членов равно 1024. Найдите знаменатель геометрической прогрессии, если известно, что он положительный.

Формула n-ого члена: $$ a_{n}=a_{1}*q^{n-1} $$

Выражаем $$ a_{2},a_{3},a_{4} $$:

$$ a_{2}=a_{1}*q^{2-1}=2*q\\a_{3}=a_{1}*q^{3-1}=2*q^2\\a_4=a_1*q^{4-1}=2*q^3 $$ 

$$ a_{1}*a_{2}*a_{3}*a_{4}=1024 $$ Подставим сюда то что выражали выше.

$$ 2*2*q*2*q^2*2*q^3=1024\\16q^6=1024\\q^6=64\\q=2 $$

Ответ: q=2 

$$ a_1=2\ \ \ \ \ \ \ \ \ \ \ q>0 \\ \\ a_1*a_2*a_3*a_4=1024 \\ \\ a_1*a_1q*a_1q^2*a_1q^3=1024 \\ \\ a_1^4*q^6=1024 \\ \\ 2^4q^6=1024 \\ \\ 16q^6=1024 \\ \\ q^6=64 \\ \\ \left \{ {{q^6=64} \atop {q>0}} \right. \\ q=\sqrt[6]{64}=2 $$

Ответ: 2

1) Шестой член геометрической прогрессии с положительными членами равен 4, а четвертый равен 9. Найдите седьмой член этой прогрессии.
2) Найдите знаменатель геометрической прогрессии, для которой отношение суммы пятого и шестого членов прогрессии к сумме третьего и четвертого членов равно \( \frac{1}{9} \)
3) Первый член геометрической прогрессии равен 27, а знаменатель равен \( \frac{1}{3} \). Найдите сумму первых семи членов этой прогрессии.