в геометрической прогрессии первый член равен - страница 4
Найти знаменатель и первый член геометрической прогрессии
b2=12
b5=324
q-
b1-
Решение: B₂=12 b₅=324 q- b₁-
b₂=b₁*q=12
b₅=b₁*q⁴=324
Разделим второе уравнение на первое:
(b₁*q⁴/b₁*q)=324/12
q³=27
q³=3³
q=3
b₁*3=12
b₁=4
Ответ: b₁=4 q=3.
b₂=128 b₇=4 b₁- q-
b₂=b₁=128
b₇=b₁*q⁶=4
Разделим второе уравнение на первое:
(q₁*q⁶/b₁*q)=4/128
q⁵=1/32=1/2⁵=(1/2)⁵
q=1/2 ⇒
b₁=128/(1/2)=256
Ответ: b₁=256 q=1/2.В геометрической прогрессии (Bn), знаменатель которой положителен, b1*b2=1/27, a b3*b4=3. Найдите сумму первых четырёх членов этой прогрессии.
Решение: $$ \begin{cases} b_1b_2= \frac{1}{27} \\ b_3b_4=3 \end{cases} \\\ \begin{cases} b_1\cdot b_1q= \frac{1}{27} \\ b_1q^2\cdot b_1q^3=3 \end{cases} \\\ \begin{cases} b_1^2q= \frac{1}{27} \\ b_1^2q^5=3 \end{cases} \\\ \frac{b_1^2q^5}{b_1^2q} = \frac{3}{1/27} \\\ q^4=81 \\\ q=3 \ (q\ > \ 0) \\\ b_1^2= \frac{1/27}{q} \\\ b_1^2= \frac{1/27}{3} = \frac{1}{81} \\\ \Rightarrow (b_1)_1= \frac{1}{9} ; \ (b_1)_2=- \frac{1}{9} $$
$$ (S_4)_1= \frac{b_1(q^4-1)}{q-1} = \frac{ \frac{1}{9} (3^4-1)}{3-1} = \frac{ \frac{1}{9}\cdot 80}{2} = \frac{40}{9} =4 \frac{4}{9} \\\ (S_4)_2= \frac{b_1(q^4-1)}{q-1} = \frac{- \frac{1}{9} (3^4-1)}{3-1} = - \frac{ \frac{1}{9}\cdot 80}{2} =- \frac{40}{9} =-4 \frac{4}{9} $$
Ответ: $$ \pm 4 \frac{4}{9} $$найди первый член геометрической прогрессии и ее знаменатель, если а5-а3=-12 и а3*а1=4
Решение: a5-a3=-12; Подставим в это уравнение реккурентные формулы для соотвестствующих членов, где q - это знаменатель прогрессии.a5-a3=a1*q*q*q*q-a1*q*q=-12, следовательно, a1*q*q(q*q-1)=-12; (1)
Аналогично, подставим рекуурентные формулы для второго уравнения:
a3*a1=4; следовательно, a1*a1*q*q=4; (2),
Будем считать, что a1*q больше либо равен 0. Тогда второе уравнение a1*a1*q*q=4; (2), можно преобразовать в a1*q=2, а это выражение в свою очередь можно подставить в уравнение (1).
a1*q*q(q*q-1)=-12;
следовательно,
2*q(q*q-1)=-12;
2q*q*q-2q+12=0;
Легко подбирается корень -2;
2q*q*q + 4q*q - 4q*q - 8q + 6q +12=0;
2q*q(q+2) - 4q(q+2) + 6(q+2)=0;
(q+2)(2q*q-4q+6)=0;
D/4=m*m-a*c=4-12<0, следовательно, уравнение не имеет вещественных корней.
Следовательно, выражение2q*q*q-2q+12=0 имеет единственный вещественный корень q=-2;
Следовательно a1*q=2=a1*(-2), следовательно, a1=-1.
Вот один вариант решения: a1=-1; q=-2;Будем считать, что a1*q меньше 0. Тогда второе уравнение a1*a1*q*q=4; (2), можно преобразовать в a1*q=-2, а это выражение в свою очередь можно подставить в уравнение (1).
a1*q*q(q*q-1)=-12;
следовательно,
-2*q(q*q-1)=-12;
2q*q*q-2q-12=0;
Легко подбирается корень 2;
2q*q*q-4q*q+4q*q-8q+6q-12=0;
2q*q(q-2) + 4q(q-2) + 6(q-2)=0;
(q-2)(2q*q+4q+6)=0;
D/4=m*m-a*c=4-12<0, следовательно, уравнение не имеет вещественных корней.
Следовательно, выражение 2q*q*q-4q*q+4q*q-8q+6q-12=0 имеет единственный вещественный корень q=2;
Следовательно a1*q=-2=a1*(-2), следовательно, a1=-1.
Вот один вариант решения: a1=-1; q=2;Ответ: 1) a1=-1; q=-2;
2) a1=-1;q=2.
Сумма первых 4 членов геометрической прогрессии равна 45. Знаменатель прогрессии равен 2. Найти сумму первых 8 членов
Решение: S4=b1+b2+b3+b4=b1+b1q+b1q^2+b1q^3
45=b1(1+2+4+8)
45=15b1
b1=3
S8=b1(q^8-1)/(q-1)=3(2^8-1)/(2-1)=3(256-1)=3*255=765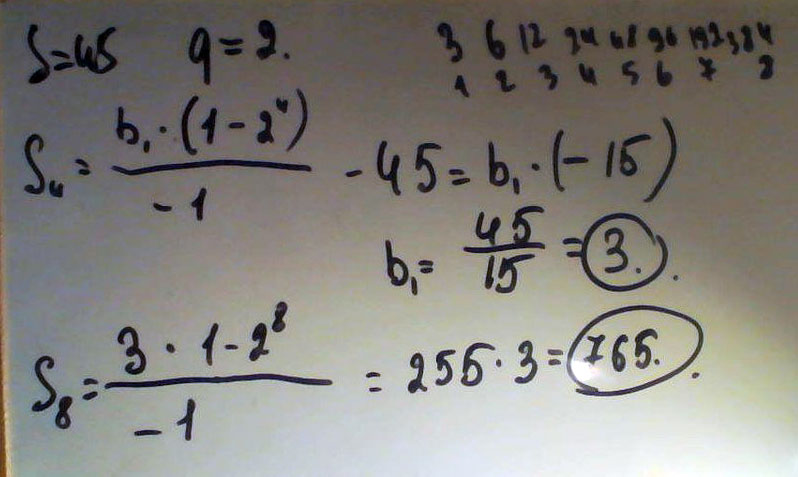
1. Определите первый член геометрической прогрессии, если её знаменатель равен 4, а восьмой член равен 256.
2. Первый член геометрической прогрессии равен 2058, а четвёртый член равен 6. Найдите знаменатель этой прогрессии.
3. Первый член конечной геометрической прогрессии, состоящей из шести членов, равен 768, последний член прогрессии меньше четвёртого в 16 раз. Найдите сумму всех членов прогрессии.
Решение: 1) $$ b_{1}=2058 $$
$$ b_{4} =6 $$
$$ q=? $$
$$ b_{4} =b_{1} * g^{4-1} =b_{1} * g^{3} $$
$$ g^{3}= \frac{b_{4}}{b_{1}} $$
$$ g^{3}= \frac{2058}{6} =343 $$
$$ q=7 $$
3) $$ b_{1}=768 $$
$$ b_{6}=b_{4}*16 $$
найти: \( S_{6} \)
решение:
$$ b_{n}=b_{1}* q^{n-1} \\ b_{4}=b_{1}* q^{3} \\ b_{6}=b_{1}* q^{5} \\ b_{1}* q^{5} =b_{1}* q^{3} *16 \\ \frac{b_{1}* q^{5} }{b_{1}* q^{3}} = 16 \\ q^{2} =16 \\ q=4 $$ или $$ q=-4 \\ S_{6} = \frac{ b_{1}(q^{6}-1) }{q-1} = \frac{768*( 4^{5} -1)}{4-1} =\\= \frac{768(1024-1)}{3} =256*1023=261888\\ S_{6} = \frac{ b_{1}(q^{6}-1) }{q-1} =\\= \frac{768*( (-4)^{5} -1)}{-4-1} = \frac{768(-1024-1)}{-5} =\\=\frac{768(-1025)}{-5} =768*205=157440 $$