в геометрической прогрессии первый член равен - страница 44
№202(А)
если : b1=6, q=2, то найдите первые пять членов геометрической прогрессии.
№203(б, в)
являются ли геометрическими прогрессиями заданные числовые ряды:
б)1;1,1;1,11;1,111;
в)-1;10;-100;1000;-10000?
№209
в геометрической прогрессии всего n членов:
а) какой номер имеет четвертый член?: б) каков номер k-го члена от конца, если члены занумерованы от начала?
Решение: b2=b1*q=6*2=12b3=b1*q^2=6*4=24
b4=b1*q^3=48
b5=b1*q^4=6*16=96
$$ 202a $$
$$ b_2=b_1*q=6*2=12 $$
$$ b_3=b_2*q=12*2=24 $$
$$ b_4=b_3*q=24*2=48 $$
$$ b_5=b_4*q=48*2=96 $$
$$ 203b $$
$$ \frac{1,1}{1}eq \frac{1,11}{1,1} $$
$$ net $$
$$ 203v $$
$$ \frac{10}{-1}=\frac{-100}{10}=\frac{1000}{-100}=\frac{-10000}{1000}=-10 $$
$$ da $$
$$ 209 $$
$$ a)4 $$
$$ b)n-k+1 $$
Выписаны первые несколько членов геометрической прогрессии -250.150.90. Найти 5 член
Решение: Посчитайте разницу между числами и прибавляйте ее к следующему числу, до тех пор пока не дойдете до 5.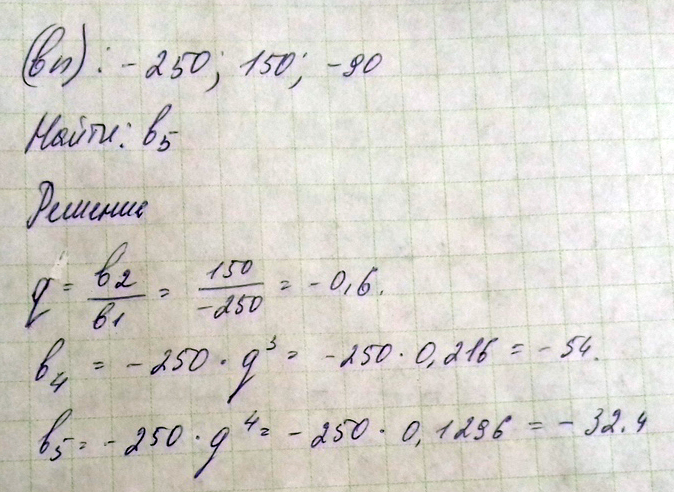
Выписаны первые несколько членов геометрической прогрессии: -84; 42; -21;. Найдите её пятый член.
Решение: Решение: Вычисление любого члена геометрической прогрессии осуществляется по формуле b(n) = b(1) * q^(n-1).
1) Вычисляем q. Пусть n=2, тогда b(1) = -84, b(2) = 42. Подставляем в формулу. 42 = (-84) * q^(2-1). Отсюда q = -1/2.
2) Вычисляем 5-й член прогрессии:
b(5) = (-84) * (-1/2)^(5-1) = (-84) / (2^4) = -84/16 = -5,25.
Ответ: -5,25.
Найти первый член геометрической прогрессии, если сумма первых трех членов равно 10, в то время как разница между первым и четвертым элементами составляет 31,5.
Решение: Использованы: формулы геометрической прогрессии (формула n-го члена), формула разности кубов, решение системы способ деления одного уравнения на другое, арифметические преобразования. Но: ответ получился странный. Может, какая-то опечатка в условии?
Даны две различные геометрические прогрессии, первые члены которых равны 1, а сумма знаменателей равна 3.
Найдите сумму пятых членов этих прогрессий, если сумма шестых членов равна 573.
Решение: $$ b_{1}=b_{1’}=1\\ q+q’=3\\ b_{6}+b_{6’}=573\\ \\ b_{1}q^{5}+b_{1}’q^{5’}=573\\ q^{5}+q^{5’}=573\\ q+q’=3\\ \\ q=3-q’\\ (3-q’)^{5}+q^{5’}=573\\ q^{5}+q^{5’}=573\\ q+q’=3\\ \\ q=3-q’\\ (3-q’)^{5}+q^{5’}=573\\ 5q^{4’} - 30q^{3’}+90q^{2’}-135q’+81=191\\ 5q^{4’}-30q^{3’}+90q^{2’}-135q’-110=0\\ 5(q^{4’}-6q^{3’}+18q^{2’}-27q’-22)=0\\ (q^{2’}-3q’-2)(q^{2’}-3q’+11)=0\\ q^{2’}-3q’-2=0\\ D=9+4*1*2=\sqrt{17}^{2}\\ q’=\frac{3+\sqrt{17}}{2}\\ q=\frac{3-\sqrt{17}}{2}\\ b_{5}=q^{4}=\frac{3+\sqrt{17}}{2}^{4}\\ b_{5}’=q^{4’}=\frac{3-\sqrt{17}}{2}^4\\ S=\frac{3+\sqrt{17}}{2}^4+\frac{3-\sqrt{17}}{2}^4=161 $$
Ответ 161