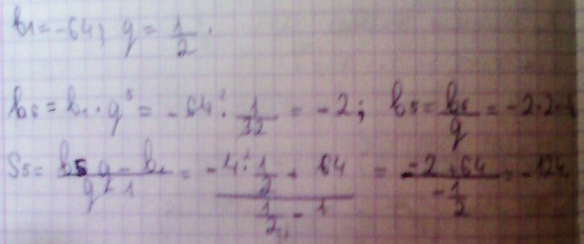в геометрической прогрессии первый член равен - страница 51
Найти шестой член геометрической прогрессии и сумму пяти первых членов геометрической прогрессии, если В1 = -64, А Q = 1/2
Решение: B6=B1*Q^5
B6=-64*0.5^5
B6=-2
S5=(B1*(1-Q^5))/(1-Q)
S5=((-64)*(1-0.5^5))/1-0.5
S5=-124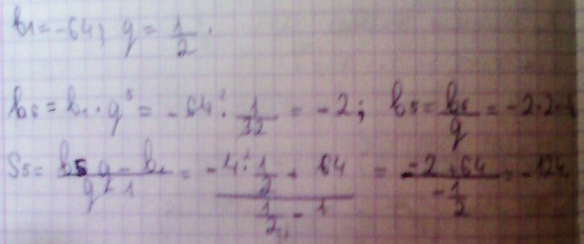
найти первый член геометрической прогрессии состоящей из 6 членов, если суммы первых и последних трех членов соответственно равны 112 и 14
Решение: Система{a1+a2+a3=112
{a4+a5+a6=14
{a1+a1*q+a1*q^2=112
{a1*q^3+a1*q^4+a1*q5=14
{a1(1+q+q^2)=112
{a1q^3(1+q+q^2)=14
a1(1+q+q^2)/a1q^3(1+q+q^2)=112/14
1/q^3=8
q=0.5(знаменатель)
Теперь подставляем в уравнение: a1+0.5a1+0.25a1=112
1.75a1=112
a1=64
заданы три первых члена числовых последовательностей. Известно, что одна из этих последовательностей-геометрическая прогрессия. укажите ее.
а. 1, 2,1.
б. 5, 1, 1/5.
в. 3, 6, 9.
г. 16, 14, 12.
Решение: ответ - бпочему?
чем отличаются арифметическая и геометрическая прогрессии.
первая получается ходом прибавления или вычитания одного и того же числа
а вторая - умножением или делением.
первая последовательность является последовательностью чисел 1 и 2, не относящихся ни к арифм. не геом. погрессиям
в и г - арифметические т. к. образуются путем прибавления и вычитания одного и того же числа.
а б - путем деление на 5.
это ответ б
там все на 5 делят
Последовательность b(n)- геометрическая прогрессия. Найдите сумму первых пяти ее членов, если b3=8, b4=16.
Решение: q=b4:b3=16:8=2- знаменатель геметрической прогрессииb5=b4*2=16*2=32-пятый член прогрессии
b2=b3:2=8:4=4- второй член
b1=b2:2=4:2=2-первый член
-
Сумму первых пяти членов геометр. прогрессии можно найти по формуле
$$ S_n=\frac{b_nq-b_1}{q-1} $$
В данном случае мы можем сложить все 5 членов этой прогрессии:
S5=2+4+8+16+32=62.
Ответ: S5=62.
1) Так как нам известно, что b₃=8, a b₄=16, можно найти знаменатель геометрической прогрессии:
q=b₄/b₃=2;
2) b₁=b₃/q²=2;
3) b₅=b₄*2=32;
4) S₊=b₁*(1-q⁺)/(1-q) ⇒ S₅=2*(-31)/(-1)=62.
Ответ: S₅=62.
(bn)- геометрическая прогрессия, знаменатель прогрессии равен 1/7, b1 = 343.
Найдите сумму первых пяти ее членов.
Решение: Сумма первых n членов геометрической прогрессии находится по формуле: $$ S= \frac{b_1q^n-b_1}{q-1} $$
подставим известные значения в формулу и найдем сумму первых пяти членов
$$ S= \frac{343*(\frac{1}{7})^5-343}{\frac{1}{7}-1}=\\=\frac{343*\frac{1}{7^5}-343}{-\frac{6}{7}}=-\frac{7*7^3*\frac{1}{7^5}-7*7^3}{6}=\\=-\frac{\frac{1}{7}-7^4}{6}=\frac{\frac{7^5-1}{7}}{6}= \\ =\frac{\frac{7^5-1}{7}}{6}= \frac{2801}{7} $$
ответ: 2801/7