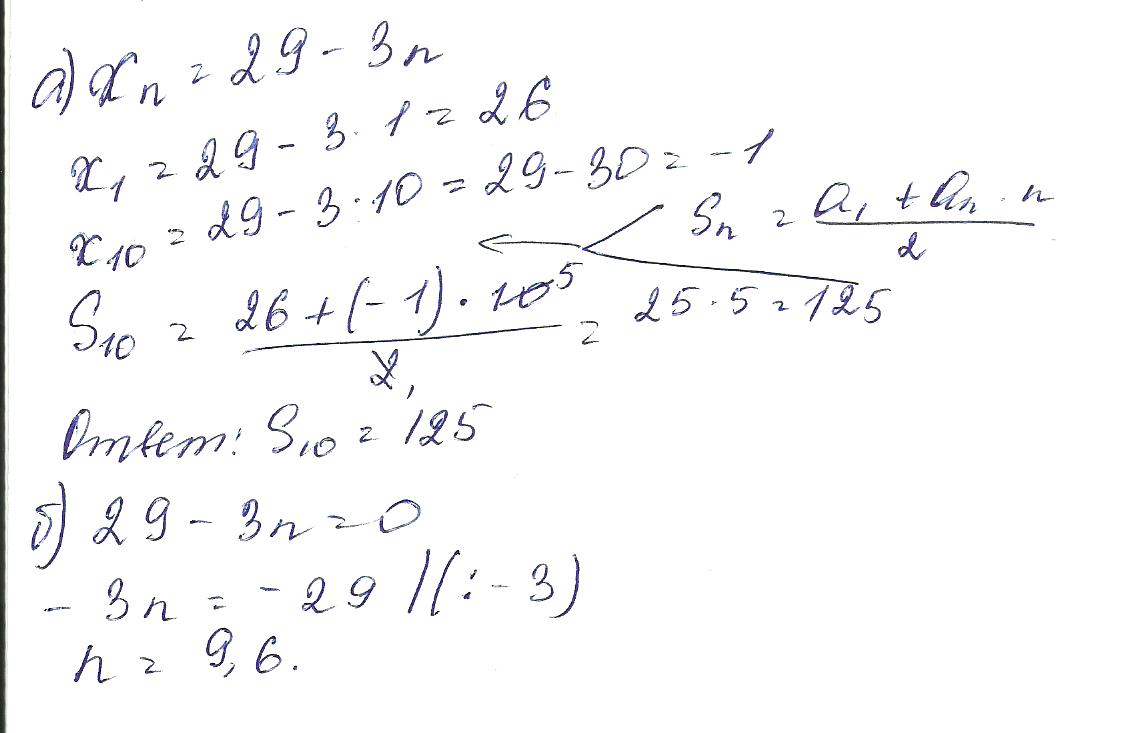прогрессия »
прогрессия задана формулой - страница 3
Арифметическая прогрессия задана формулой n=29-3n а) Найдите сумму первых 10 членов б) сколько в данной прогрессии положительных членов?
Решение: $$ n=29-3n $$
$$ n_1=29-3\cdot1\\ n_1=26\\\\ n_{10}=29-3\cdot10\\ n_{10}=-1\\\\ S_n=(a_1+a_n)\cdot \frac{n}{2} \\\\ S_{10}=(26-1)\cdot \frac{10}{2}=5\cdot(26-1)=125 $$
Так как только 10 член арифметической прогрессии отрицателен, значит, все 9 оставшихся членов положительны.
Ответ: $$ a) \ S_n=125; $$ б) $$ 9 $$А)Sn=a1+an:2*n. S10=a1+a10:2*10. a1=29-3=26. a10=29-30=-1. S10=25:2*10=12,5*10=125. Ответ:S10=125. б)29-3n>0.3n>-29. n<9,6. Ответ: х=9.
Арифметическая прогрессия задана формулой a n=-3n+10. Укажите число, которое НЕ является членом прогрессии
Решение: Вместо a₂ подставляем числа 7; -5; 13; 4 и получаем значение n
7=-3n+10; 3n=3; n=1 Число7 является членом прогрессии
-5=-3n+10 3n=15 n=5 Число -5 является членом прогрессии
13=-3n+10 3n=-3 n=-1 Число 13 не является членом прогрессии
4=-3n+10 3n=6 n=2 Число 4 является членом прогрессии
Арифметическая прогрессия задана формулой
Хn = 29-3n.
а) Найдите сумму первых 10 членов прогрессии.
б) Сколько в данной прогрессии положительных членов? если можно, то решением)
Решение: Задание "б". за правильность не ручаюсь, т. к. в школе этого не проходили еще. мое решение по образцу. здесь n=9,6 округляем до 9, значит в данной прогрессии 9 положительных членов.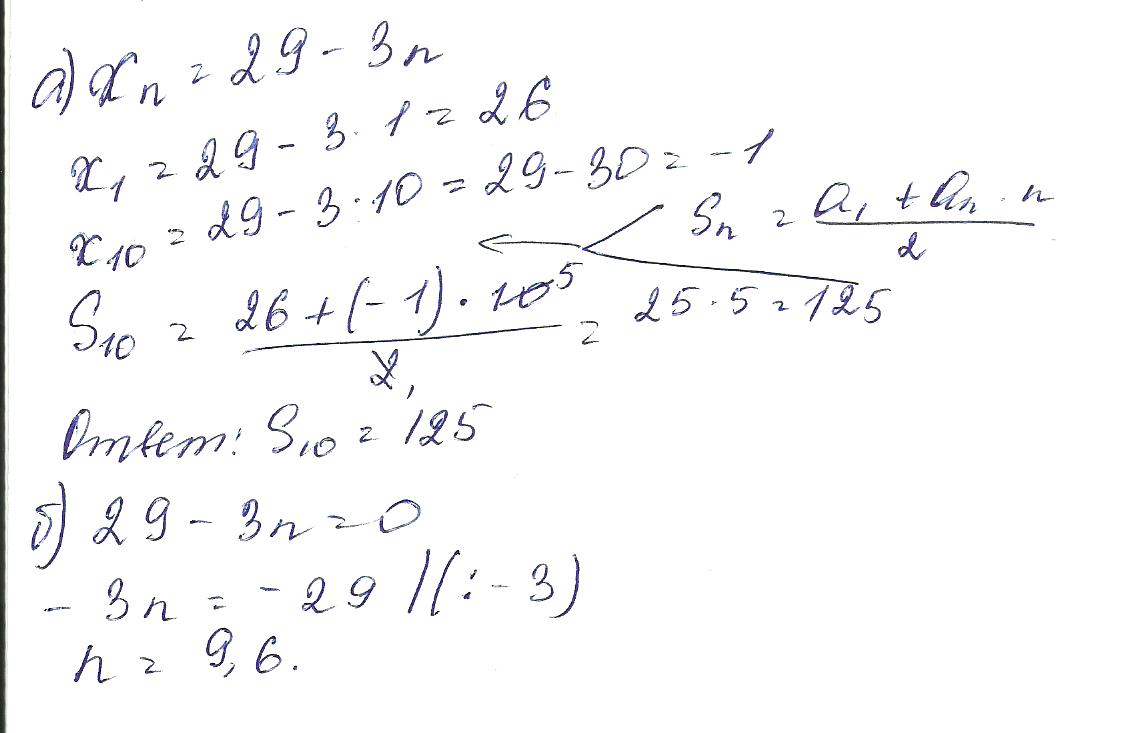
Арифметическая прогрессия задана формулой Аn=3n+5
Найдите: S10; S20 ; Sn.
Решение: Эта прогрессия задана рекурентно.Найдем первый, второй член, разность,10 член и 20 член
1)a1=3*1+5=3+5=8
2)a2=3*2+5=6+5=11
3)d=a2-a1=11-8=3
4)a10 = a1+9d=8+3*9=8+27=35
5)a20=a1+19d = 8+3*19=8+57=65
6)S10= (a1+a10)/2 *10 = (8+35)*5 = 215
7)S20=(a1+a20)/2 *20 =(8+65)*10 = 73*10=730
8)Sn = n(a1+an)/2
Аn=3n+5
a1=3*1+5=8
a2=3*2+5=11
d=a2-a1=11-8=3
Решение:
S10
найдём для начала a10
a10=a1+9d=8+9*3=35
S10=(a1+a10)/2*10=(8+35)/2*10=215
S20
найдём для начала a20
a20=a1+19d=8+19*3=65
S20=(a1+a20)/2*20=(8+65)/2*20=730
1. Найдите сумму:
в) всех двузначных чисел
г) всех трехзначных чисел
2. Арифметическая прогрессия задана формулой a[n]=3[n]+5.
Найдите:
а) S[10]
б)S[20]
в)S[n]
Решение: В)
а₁=10
а₂=11
d=1
an=99
99=10+d(n-1)
n=90
S₉₀=10+99 *90= 4905
2
Г)
а₁=100
d=1
an=999
999=100+(n-1)
99+n=999
n=900
S₉₀₀=100+999 *900 =494550
2
2) a₁=3+5=8
a₁₀=35
S₁₀=8+35*10 =215
2
a₂₀=65
S₂₀=8+65*20 =730
2
Sn=8n=3n²+5n =13n+3n²
2 2