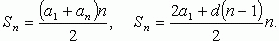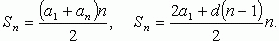прогрессия »
разность членов арифметической прогрессии - страница 25
Докажите что если d- разность арифметической прогрессии, а Xm и Xn-ее члены(m не равно n, m и n порядковый номер), то Xm- Xn=(m-n)d
Решение: Разность арифметической прогрессииd = an+1 - an
Число d называют разностью арифметической прогрессии
Числовую последовательность, каждый член которой, начиная со второго, равен сумме предыдущего члена и одного и того же числа d, называют арифметической прогрессией.
an+1 = an + d, n є NОпределите, является ли последовательность, заданная формулой n-го члена, арифметической прогрессией ( если является, то найдите её разность):
а) аn=2n+5
б)an=10-3n
в)an=n^2
г)an=-4n
Решение: Используя определение арифметической прогрессииа) аn=2n+5
$$ d=a_{n+1}-a_n=2(n+1)+5-(2n+5)=2n+2+5-2n-5=2 $$
даная последовательность - арифметическая прогрессия с разностью 2
б)an=10-3n
$$ d=a_{n+1}-a_n=10-3(n+1)-(10-3n)=10-3n-3-10+3n=-3 $$
даная последовательность - арифметическая прогрессия с разностью -3
в)an=n^2
$$ d=a_{n+1}-a_n=(n+1)^2-n^2=n^2+2n+1-n^2=2n+1 $$
не является
г)an=-4n
$$ d=a_{n+1}-a_n=-4(n+1)-(-4n)=-4n-4+4n=-4 $$
даная последовательность - арифметическая прогрессия с разностью -4
В арифметической прогрессии с разностью d девятый член = 1. Чему равно d чтобы произведение четвёртого, седьмого и восьмого членов была наибольшей?
Решение: $$ a_{9}=1\\ a_{1}+8d=1\\\\ a_{4}a_{7}a_{8}=(a_{1}+3d)(a_{1}+6d)(a_{1}+7d) =\\ (1-8d+3d)(1-8d+6d)(1-8d+7d)=(1-5d)(1-2d)(1-d)\\ f(d)=(1-5d)(1-2d)(1-d) $$
Рассмотрим функцию
$$ f(d)=(1-5d)(1-2d)(1-d)\\ f(d)=-10d^3+17d^2-8d+1\\ f’(d)=-30d^2+34d-8\\ -30d^2+34d-8=0\\ D=34^2-120*8=14^2\\ d=\frac{-34+14}{-60}=\frac{1}{3}\\ d=\frac{-34-14}{-60}=\frac{4}{5}\\ $$
функция принимает наибольшее значение в точке
$$ d=\frac{4}{5}\\ $$
Ответ $$ d=\frac{4}{5} $$В арифметической прогрессии {An} имеем a1= -85, а19 - её первый положительный член. Какие целые значения может принимать разность прогрессии?
Решение: Если d=4, то:
а19= -85+4(19-1)= -13 ; а19 отрицательный, значит разность прогрессии не 4.
если d=5, то:
а19= -85+5(19-1)= 5 ; а19 положительный, значит разность прогрессии 5.
если d=6, то:
а19= -85+6(19-1)= 23 ; а19 положительный, но не "первый положительный" как сказано в условии. (а18=17, а17=11, а16=5)
Ответ: d=5В арифметической прогрессии сумма 50 первых ее членов равна 2650, а разность равна 2. Найдите первый член этой прогрессии.
Решение: S50=(2a1+49*2)*50/2=(2a1+98)*25=50
2a1+98=50/25=2
2a1=2-98=-96
a1=-96/2=-48
По 2 формуле 2650=(2а+2(49))*50/2,
2650=(2а+98)/25
2а+98=2650/25
2а+98=106
2а=8
а=4