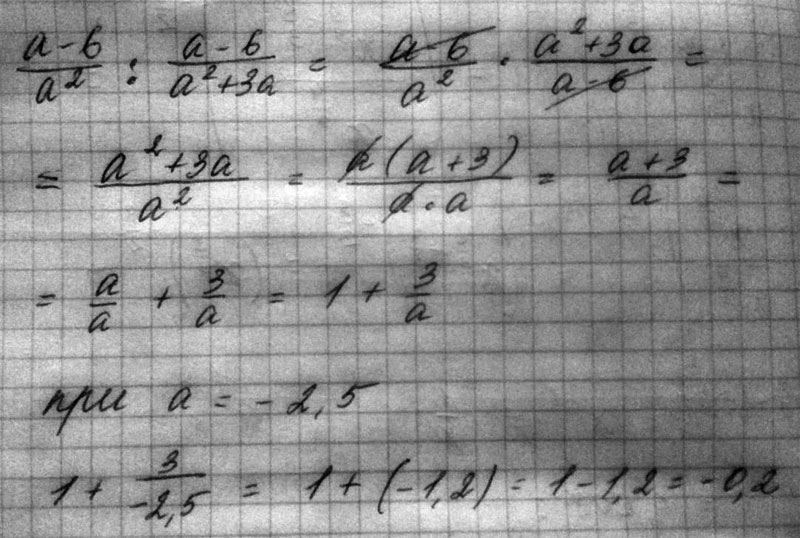найдите значение выражения
1.Найдите ошибки и исправьте их:а)-22:(-2)=-11
б)-348:120=-29
в)2807:(-24)=-205
г)330:(-11)=30
2.Найдите среднюю дневную температуру за неделю:
Понедельник. -13°С
Вторник. -9°С
Среда. -5°С
Четверг. -0°С
Пятница. -2°С
Суббота. -2°С
Воскресенье. -3°С
3.Сравните значения числовых выражений:
1733*(-69). и 1733:(-69)
Как можно выполнить это задание ,не находя значения выражений?
4.Найдите значение выражений:
2(x-5):(-4). при x= -15
Решение: A) Минус на минус дают + => Ответ 11, а не минус 11.
б) ответ -2,9, а не -29
в) -205*(-24)=4920, а не 2807
г) ответ -30, а не 30.
2. Приблизительно -7 градусов.
3. 1733*(-69) > 1733:(-69)
Посмотреть на знак, который стоит между a и b
4. 2(x-5):(-4) x=-15
30-10:(-4)=30+2.5=32.51. а)-22:(-2)=11
б)-348:120=-2,9
в)2807:(-24)=-116,9583
г)330:(-11)=-30
2. (13+9+5+0+2+2+3):7=4,85714286
3. 1733:(-69) больше
4. 2×(-15-5):(-4)=10№ 1. Вычислите, выбирая удобный порядок действий: а) 42+61+28+39+30 б) 4•9•5•2•25 № 2. Дано выражение 18•37+44 18•37+18•4437+18•44 № 3. Найдите значение выражения, вынося за скобки общий множитель: 83•17+27•17 № 6. Решите двумя способами задачу: Что бы сварить варенье из слив, берут 10 частей слив, 15 частей сахара и 2 части воды. Было приготовленно 540 кг. варенья. Сколько слив пошло на варенье? № 447.Решите двумя способами задачу: У двух мужиков 40 овец, а у одного меньше против другово на 6. Сколько у каждого?
Решение:1)а) 42+61+28+39+30=(42+28)+(61+39)+30=70+100+30=(70+30)+100=100+100=200
б)4•9•5•2•25=(4*5)*(2*25)*9=(20*50)*9=1000*9=9000
2)18*37+44=666+44=710
18*37+18*44=666+792=1458
37+18*44=37+792=829
3)83*17+27*17=17*(83+27)=17*110=1870
6)1 способ
10+15+2=27 частей варенья
540:27=20кг вес одной части
10*20=200кг слив пошло на варенье
2 способ
х-вес одной части варенья
15х+10х+2х=540
27х=540
х=540:27
х=20кг вес одной части
10*20=200кг слив пошло на варенье
447)1 способ
(40-6):2=17 овец у одного
17+6=23 овцы у другого
2 способ
х-овец у одного
х+6-овец у другого
х+х+6=40
2х=40-6
2х=34
х=34:2
х=17 овец у одного
17+6=23 овцы у другого
Найти значение выражения 1⋅1+2⋅2+3⋅3+…+9⋅9. Напомним, что 9=362880
Решение: Ответ: значение выражения равно 10!-1=10*9!-1=3628799.
Доказательство того, что 1*1!+...+n*n!=(n+1)!-1.
1)Базис индукции. 1*1!=2!-1 - верно.
2)Шагиндукции. Пусть для какого-то n это верно. Тогда прибавим к обеимчастям равенства выражение (n+1)! и преобразуем правую часть:
(1*1!+2*2!+...+n*n!)+(n+1)*(n+1)!=(n+1)!-1 +(n+1)*(n+1)!=(n+1)! * (n+1+1) -1=(n+2)!-1. Как в левой, так и вправой части получили те же выражения, что и в предположении с заменой(n) на (n+1), значит, то, что мы доказываем, верно и для n+1.
И, согласно методу математической индукции, 1*1!+...+n*n!=(n+1)!-1 при любом натуральном n.Найти значение выражения (a - 6)/a^2 : (a - 6)/(a^2 + 3a) при a=-2,5. Перед этим все возможное сократить.
Решение:=(a-6/a2)*(a2+3a/a-6)
a-6 сокращается остаётся а2+3а/а2
подставляем значение а= -2,5
(-2,5)2+3×(-2,5)/ (-2,5)2=6.25+(-7.5)/6.25=-1.25/6.25=-0.2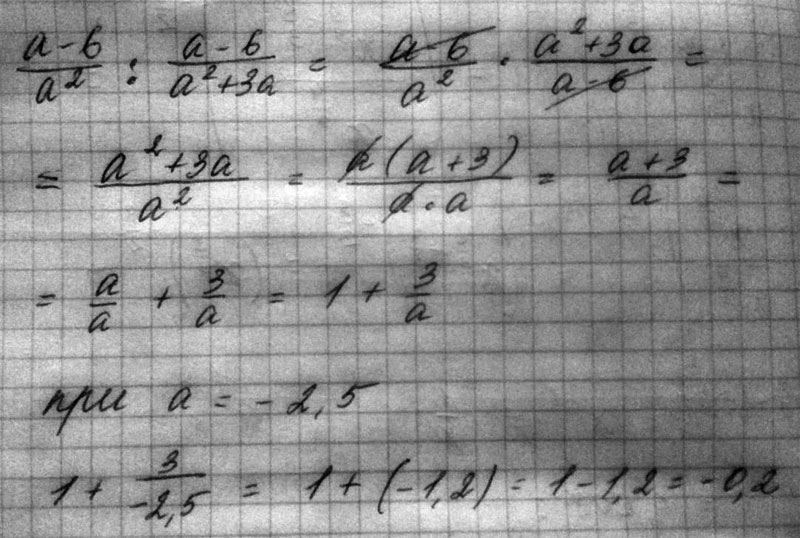
Найти значение выражения 40 в 11 степени* на 4 в -11 степени: на 10 в 10 степени
Решение:$$ \frac{40^{11}*4^{-11}}{10^{10}} = \frac{4^{11}*10^{11}*4^{-11}}{10^{10}}= \frac{4^{11-11}*10}{1}=4^0*10=1*10=10 $$
40 в 11 степени можно расписать,как (4*10)в 11 степени
сокращаем и числитель,и знаменатель на 10 в 10
при умножении степени складываются(если основания одинаковые),т.е. в числителе 4 в 11*4 в -11,четыре оставляем без изменения,а показатели складываем(11+(-11)=11-11).В степени получаем 0.ЛЮбое число в степени 0 равно 1Найдите значение выражения \( x+ \sqrt{x^{2}-4x+4 } \), при \( x \leq 2 \)
Решение: $$ x+\sqrt{x^2-4x+4}=x+\sqrt{(x-2)^2} $$
избавимся от корня:
$$ x+|x-2| $$
тут есть два варианта, оставить все как есть или поменять местами x-2...
1) x-2 остаются на своем месте:
у нас получается: $$ 2x-2 $$ - это никак не может подходить, т.к. не является значением выражения
2) x-2 поменяем местами:
у нас получается: $$ x+2-x=2 $$ - значение выражения
Ответ: 2
Найдите значение выражения, представив подкоренное выражение в виде произведения квадратов:
1) √32*98
2) √162*128
3) √0.03*75
4)√0,12*192
5)√33*15*55
6)√42*35*30
7)√63*91*52
8)√40*85*34
Решение: 1) √32*98=√16*2*49*2=√4² * √7² * √2²=4*7*2=56
2) √162*128=√81*2*64*2=√9² * √8² * √2²=9*8*2=144
3) √0.03*75=√0.01*3*25*3=√0,1² * √5² * √3²=0,1*5*3=1,5
4) √0,12*192=√0,01*12*12*16=√0,1² * √12² * √4²=0,1*12*4=4,8
5) √33*15*55=√3*11*3*5*11*5=√3² * √11² * √5²=9 * 11 * 5=495
6) √42*35*30=√6*7*7*5*6*5=√6² * √7² * √5²=6*7*5=210
7) √63*91*52=√7*9*7*13*13*4=√7² * √13² *√9 * √4=7*13*3*2=13*42=546
8) √40*85*34=√4*10*5*17*17*2=√4*2*5*5*17*17*2=
=√4*√2² * √5² * √17²=2*2*5*17=340Найдите значение выражения:1) пять целых одиннадцать сорок вторых минус две целых три четырнадцатых минус одна целая одна двадцать первых 2)одиннадцатьцелых минус шесть целых тринадцать двадцать первых минус три четырнадцатых
Решение: "1) пять целых одиннадцать сорок вторых минус две целых три четырнадцатых минус одна целая одна двадцать первых" Ответ = 2
"2)одиннадцатьцелых минус шесть целых тринадцать двадцать первых минус три четырнадцатых" Ответ = 4 целых одна шестая ( 4. 1\6)найдите значение x(в радианах) если 0
Решение: sin32+sin28 = 2sin30cos2 (формула суммы синусов).Получается, что x = 30.
sin32+sin28=2sinx*cos2
2sin(32+28)/2*cos(32-28)=2sinx*cos2
2sin30*cos2=2sinx*cos2
отсюда видно, что x=30
30 градусов, это П/6
Ответ:П/6
2000-1999+1998-1997+1996...+2-1 найти значение
Решение:2000-1999+1998-1997+1996...+2-1
Разбиваем выражение на скобки
(2000-1999)+(1998-1997)+(1996...+(2-1)
Так как в каждой скобке по 2 слагаемых, то всего 1000 скобок. Разность каждой скобки равна 1, значит
1+1+1+...(1000 раз)...+1=1000
Ответ: 1000В данной сумме участвует 2000 чисел, сгруппируем по парам (2000-1999) + (1998-1997)+ ...+(2-1), значение одной такой пары равно 1,а всего пар 2000 : 2=1000
Значит 2000-1999+1998-1997+....+2-1=1000 *1=1000
Ответ : 1000
