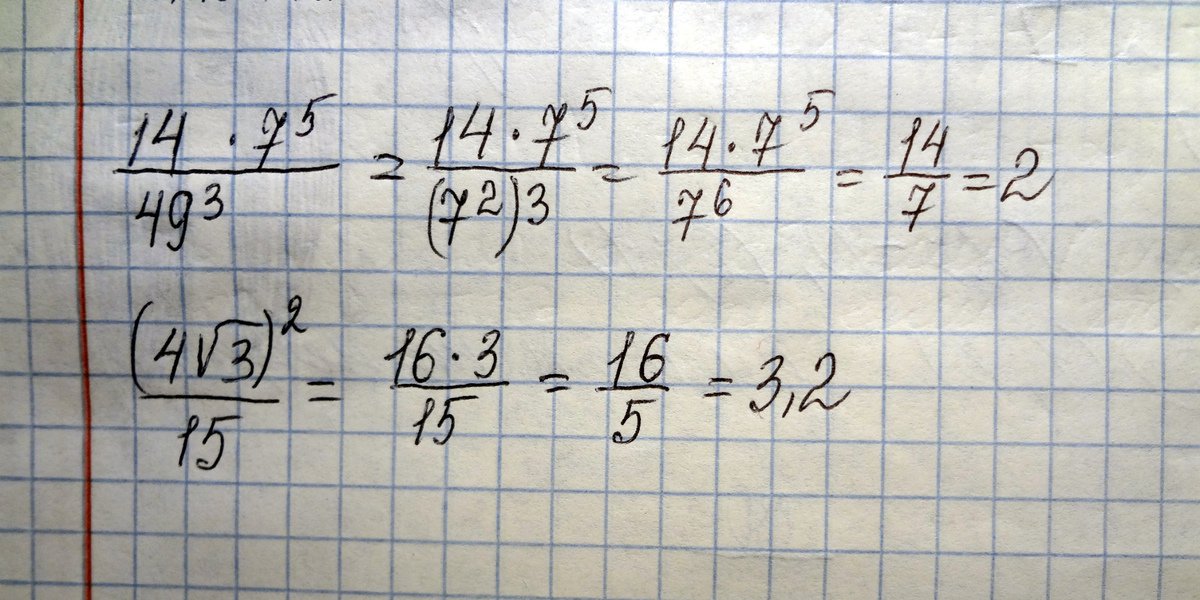найти значение »
найдите значение выражения - страница 3
Найти значение выражения: 1) \( 5\sqrt{6x-2} \) где x=1, x= \( \frac{1}{3} \), x=3
2) Решить уравнение: 1) \( \sqrt{x}=2 \) 2) \( \sqrt{x}=10 \)
Решение: 5*корень( 6*х-2) {при х=1} = 5*корень( 6*1-2)= 5*корень( 4) = 10
5*корень( 6*х-2) {при х=1/3} = 5*корень( 6*1/3-2)= 5*корень( 0) = 0
5*корень( 6*х-2) {при х=3} = 5*корень( 6*3-2)= 5*корень(16) = 20
2)
корень( х )= 2
x=2^2=4
3)
корень( х )= 10
x=10^2=10
((3 sqrt(c)^2)-4)/(3 sqrt(c)+2-c^1/3 - УПРОСТИТЬ (sqrt это корень квадратный)
(sqrt(3))*(3sqrt(8)-2*(3^1/2) НАЙТИ ЗНАЧЕНИЕ ВЫРАЖЕНИЯ
3*sqrt(2) *2^0,5-(4sqrt(16)) НАЙТИ ЗНАЧЕНИЕ ВЫРАЖЕНИЯ
x^1/3+((9-x^3)/(3+x^1/3) УПРОСТИТЬ
((25-sqrt(k))/(5+(4sqrt(k))+k^1/4 УПРОСТИТЬ
Решение: 33.
$$ \frac{25-\sqrt{k}}{5+\sqrt[4]{k}}+k^\frac{1}{4}=\\=\frac{5^2-(\sqrt[4]{k})^2}{5+\sqrt[4]{k}}+\sqrt[4]{k}=\frac{(5-\sqrt[4]{k})(5+\sqrt[4]{k})}{5+\sqrt[4]{k}}+\sqrt[4]{k}=\\=5-\sqrt[4]{k}+\sqrt[4]{k}=5 $$
31.
$$ 3\sqrt{2}*2^{0.5}-\sqrt[4]{16}=3\sqrt{2}*\sqrt{2}-\sqrt[4]{2^4}=3*2-2=4 $$
32.
$$ x^\frac{1}{3}+\frac{9-x^\frac{2}{3}}{3+x^\frac{1}{3}}=\\=x^\frac{1}{3}+\frac{3^2-(x^\frac{1}{3})^2}{3+x^\frac{1}{3}}=\\=x^\frac{1}{3}+\frac{(3-x^\frac{1}{3})(3+x^\frac{1}{3})}{3+x^\frac{1}{3}}=\\=x^\frac{1}{3}+3-x^\frac{1}{3}=3 $$
30.
$$ \sqrt{3}*\sqrt[3]{8}-2*3^\frac{1}{2}=\\=\sqrt{3}*\sqrt[3]{2^3}-2\sqrt{3}=\\=2\sqrt{3}-2\sqrt{3}=0 $$
29.
$$ \frac{\sqrt[3]{c^2}-4}{\sqrt[3]{c}+2}-c^\frac{1}{3}=\\=\frac{(\sqrt[3]{c})^2-2^2}{\sqrt[3]{c}+2}-\sqrt[3]{c}=\\=\frac{(\sqrt[3]{c}-2)(\sqrt[3]{c}+2)}{\sqrt[3]{c}+2}-\sqrt[3]{c}=\\=\sqrt[3]{c}-2-\sqrt[3]{c}=-2 $$
3ас^2 / а^2 - 16с^ * а - 4с / ас при а=2,1 с=-0.4 найти значение выражения
Решение: $$ \frac{3ac^{2} }{ a^{2}-16 c^{2}} \cdot \frac{a-4c}{ac} =\\= \frac{3ac^{2} \cdot (a-4c)}{(a-4c)(a+4c)\cdot ac} =\\= \frac{3c}{a+4c}= \frac{3*(-0,4)}{2,1+4\cdot(-0,4)}= \frac{-1,2}{0,5} =-2,4 $$
При а=2,1; с=-0,4
Ответ: -2,4Найдите значение выражений: 14 * 49^(-3) * 7^5, (4 * sgrt3)^2 / 15
Решение: 14 * 49^(-3) * 7^5 = 7 * 2 * (7^2)^(-3) * 7^5= 2*7^1 * 7^(-6)* 7^5 =
=2 * 7^(1-6+5)= 2 * 7^0 = 2*1 = 2.
2) (4 * sgrt3)^2 / 15 = 4^2 * 3 / 15 = 16*3/15 = 16/5 = 3,2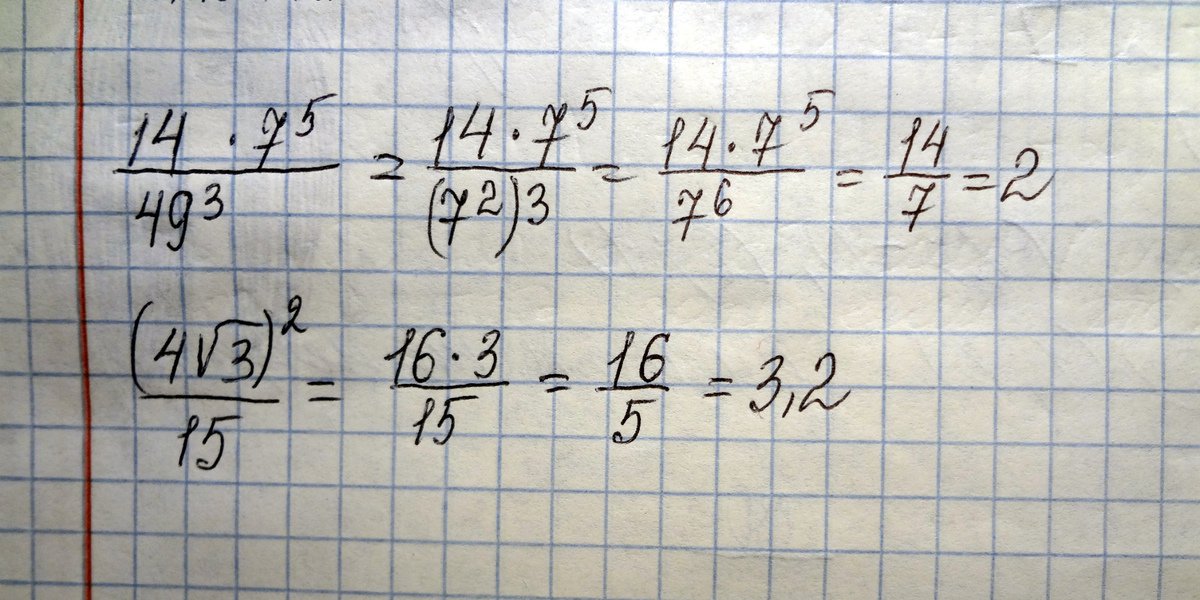
Найдите значение выражений: log₆18+log₆2; 15^(3,4) / 5^(0,4)*3^(3,4); log₃m^(5/8); log₃256* log₂(1/81) / ( log₅(1/16)* log₄125; log₂lg100
Решение: В 1)переходим к равносильному 18+2 = 20 т.к основания одинаковые
3)40 5/8
1) log₆18+log₆2 = log₆(18*2) = log₆36 = log₆6² = 2.
2) 15^(3,4) / 5^(0,4)*3^(3,4) = 5^(3,4)*3^(3,4) / 5^(0,4)*3^(3,4) =
= 5^(3,4-0,4) = 5³ = 125.
3) log₃m^(5/8) = (5/8)* log₃m =(5/8)*40 = 25 (так как log₃m = 40).
4) log₃256* log₂(1/81) / ( log₅(1/16)* log₄125 =
= log₃2⁸* log₂(3⁻⁴) / ( log₅(2⁻⁴)* log₄5³ =
= 8log₃2*(-4) log₂3 / ((-4)log₅2)* (3/2)log₂5 =
= -32log₃2*(1/ log₃2) / ((-6)log₅2)* (1)/log₅2) = 32 / 6 = 16 / 3 = 5(1/3).
5) log₂lg100 = log₂lg10² = log₂2 = 1.