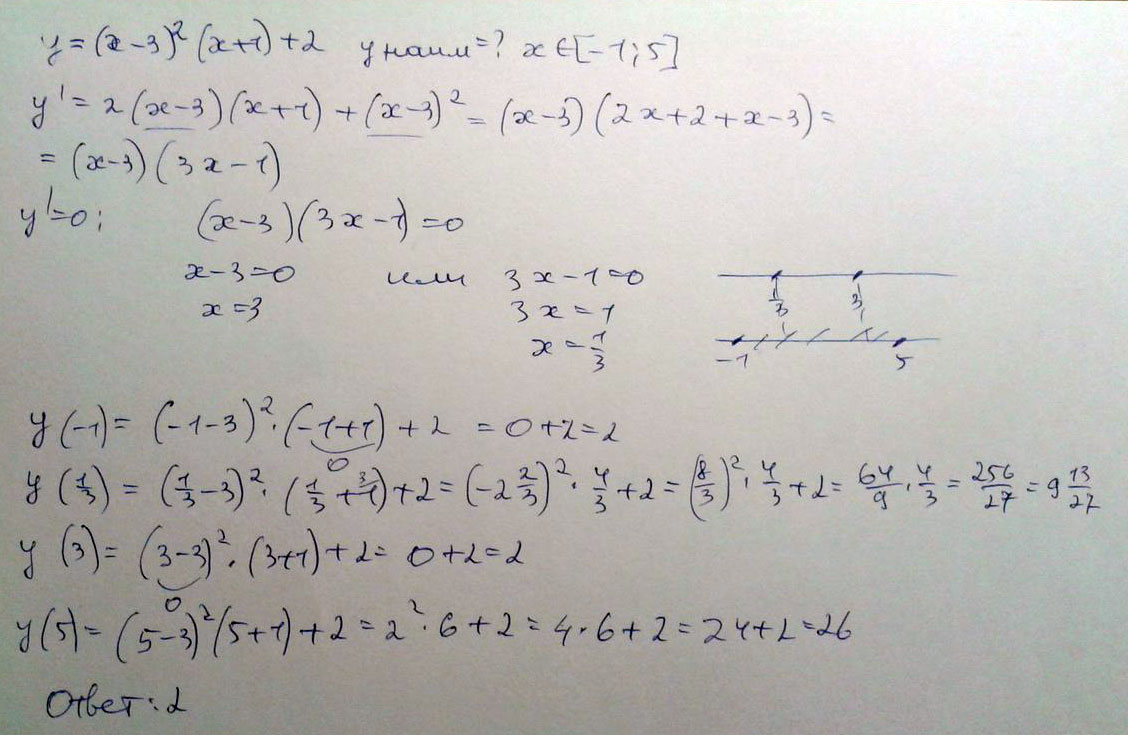найти значение »
найдите наименьшее значение функции y - страница 3
Найдите наименьшее значение функции y=x во второй степени +2 на отрезке [-2;1]
Решение: Имеем ф-цию у = х² + 2 на отрезке [-2; 1]Найдем наименьшее значение функции:
при х = -2 : у = (-2)² + 2 = 6;
при х = -1 : у = (-1)² + 2 = 3;
при х = 0 : у = 0² + 2 = 2;
при х = 1 : у = 1² + 2 = 3.
наименьшее значение функции есть при х = 0, у = 2
y=x²+2
p=-b/2a
q=-0/(2*1)
q=0
вершина параболы принадлежит отрезку
y_min=0²+2=2
найдите наименьшее значение функции y=sin^2x + sinx +1
Решение: Решение по алгоритму: 1) находим критические точки
2) вычисляем значение функции в них
3) выбираем наименьшее из них
Найдите наименьшее значение функции y=(x-3)^2(x+1)+2 на отрезке [-1:5]
Решение: $$ y’=2( x^{2} -2x-3)+(x-3)^2 y’=3x^2-10x+3 \\ 3x^2-10x+3=0 \\ D=64 \\ x1=3 \\ x2= \frac{1}{3} $$
Подставив в исходное уравнение полученные результаты и данные концы определяемого отрезка, получим, что при х=3,у=2 - наименьш. знач.
Ответ:уЄ{2}
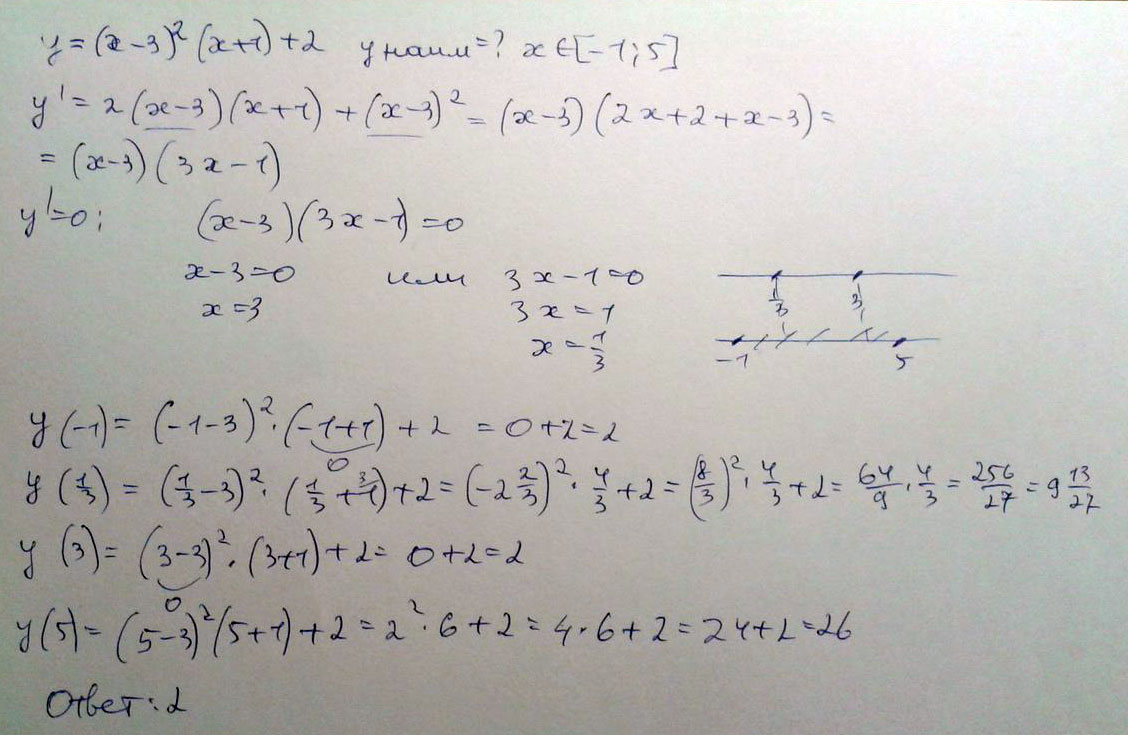
Найдите наименьшее значение функции y=√x²-16x+185
Решение: $$ f(x) = x^2 - 16x + 185 $$ - это парабола, ветви которой направлены вверх. Соответственно, если вершина этой параболы будет лежать в области определения функции y (т.е. будет выше оси абсцисс), то именно в ней достигается наименьшее значение. Если у этой параболы есть корни, то наименьшее значение функции будет равно нулю (т.к. выражение под корнем не может быть меньше нуля). Дабы убедиться, что корней нет, проверим дискриминант:
$$ D = b^2 - 4ac = (-16)^2 - 4*185 = 256 - 740 < 0 $$
Вещественных корней нет, будем искать координаты вершины.
$$ x_v = -\frac{b}{2a} = \frac{16}{2} = 8\\ f_v = f(x_y) = (8)^2 - 16*8 + 185 = 64 - 128 + 185 = 121 $$
Теперь, максимальное значение нашей функции $$ y=\sqrt{f_v} = \sqrt{121} = \boxed{11} $$Найдите наименьшее значение функции y=1/(-x^2+ax-4), если график этой функции проходит через точку М(3;-1/11)
Решение: y=1/(-x²+ax-4)
Функция проходит через точку М(3;-1/11) следовательно:
-1/11=1/(3a-13)
3a-13=-11⇒a=2/3
y=1/(-x^2+2/3x-4)
Рассмотрим знаменатель:
-x²+2/3x-4=-(х²-2·1/3·x+1/9-1/9+4)=-(x-1/3)²-35/9<0
Так как дробь принимает отрицательные значение, то наименьшее значение функция будет принимать когда знаменатель по модулю наименьший⇒
(x-1/3)²+35/9⇒наименьшее значение 35/9
Значит наименьшее значение функции: -9/35