найти значение »

найдите наибольшее значение функции на отрезке

  • Квадратный трехчлен ax²+bx+c (a,b и c – действительные числа) имеет два различных ненулевых корня: 1 и q. После того, как Никита изменил значение какого-то из коэффициентов: a, b или c, получился трехчлен, имеющий два различных корня: 2 и 3q. Найдите наибольшее значение q.


    Решение: Так как корни квадратного уравнения $$ ax^2+bx+c $$ являются числа $$ 1;q $$, то данный трехчлен можно представить в виде 
    $$ (x-1)(x-q)=x^2+x(-q-1)+q $$ , по второму условию следует что можно представить в виде 
    $$ x^2+x(-3q-2)+6q $$ , по условию он поменял только одну переменную , очевидно что $$ 6q>q $$ , тогда следует что только 
    $$ -q-1=-3q-2 q=-0.5 $$

  • 1. Найдите точки пересечения параболы y=x^2 и прямой y= - 2x
    2. Не выполняя построений графика, найдите наибольшее или наименьшее значения функции y= -2x на отрезке [1, 4/3].
    3. С помощью графика функции y=-x^2 определите, при каких значениях x верно неравенство y>-9


    Решение: 1. 
    $$ x^{2} = -2x $$
    $$ x(x + 2) = 0 $$
    $$ x_{1} = 0 => y_{1} = 0 $$
    $$ x_{2} = -2 => y_{2} = 4 $$
    Ответ: (0;0), (-2;4)
    2.
    Функция y=-2x - линейная, монотонно убывающая. Значит, наибольшему значению x соответствует наименьшее значение y. На отрезке [1; 4/3] наименьшему значению y будет соответствовать x = 4/3. $$ y_{min} = -2 * \frac{4}{3} = - \frac{8}{3} $$
    Наибольшему значению y будет соответствовать x = 1. $$ y_{max} = -2 * 1 = -2 $$
    3. График прикреплен
    Ответ: x∈(-3; 3)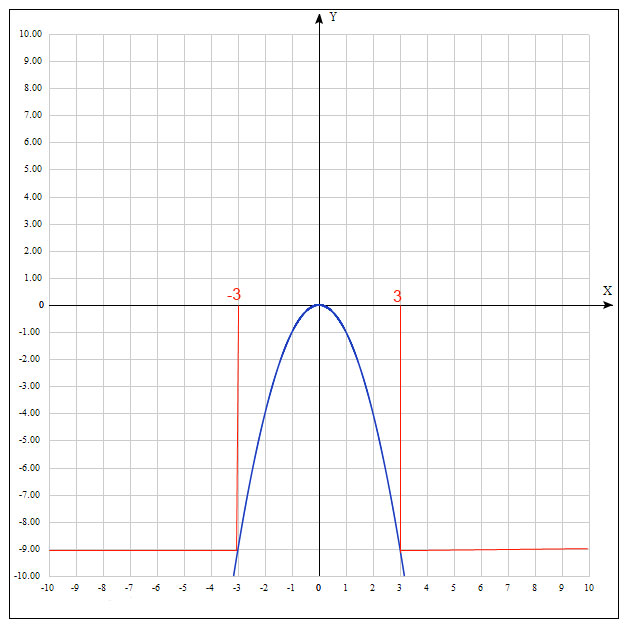.  x - x x x x y x - y Ответ - .Функция y - x - линейная монотонно убывающая. Значит наибольшему значению x соответствует наименьшее значение y. На отрезке наименьшему знач...

  • Найдите наибольшее значение функции y=5 - 8x - 4x^2. Варианты ответов: 1)9; 2)7; 3)5; 4)12; 5)15


    Решение: Это уравнение квадратичной функции, графиком которой является парабола, перепишу в стандартном виде y=-4x² - 8x+5, так как а=-4<0 (вообще коэффициенты соответственно равны а=-4, b=-8, c=5, то ветви вниз, и значит действительно у параболы будет наибольшее значение (а вот наименьшего не будет, так как веточки параболы уйдут в ∞), координата х вершины параболы определяется по формуле х0=-b/2a=-(-8)/(2*(-4)=8/(-8)=-1, тогда у0=у(х0)=у(-1)=-4*(-1)² -8*(-1)+5=-4+8+5=9 это и есть наибольшее значение функции, ответ номер 1

  • Найдите наибольшее значение функции y=10+6x-2x^3/2 на отрезке [1; 15]


    Решение: Найдем производную y’=6-3*x^(1/2). Решим уравнение y’=0, тогда x^(1/2)=2, значит x=4. При х принадлежащих интервалу (1;4) производная принимает положительные значения, т.е. y’>0, значит функция возрастает. При х принадлежащих интервалу (4;15) производная принимает отрицательные значения, т.е. y’<0, значит функция убывает. Получили, что x=4 - точка максимума. У(4)=10+24-16=18. Ответ: 18.

  • Найдите наибольшее значение функции y=24tgx - 24x + 6п - 3 на отрезке [-п/4; п/4] .


    Решение: Y’=(24tgx-24x+6π-3)’=24*(1/(cosx)²)-24=24/(cosx)²-24
    y’=0, 24/(cosx)²-24=0, 24/(cosx)²=24
    (cosx)²=1
    1. cosx=-1 2.  cosx=1
    x₁=π+2πn, n∈Z x₂=2πn, n∈Z
    x₁=π+2πn∉[-π/4;π/4]
    вычислить значения функции в точках: -π/4; 0; π/4
    y(-π/4/)=24*tg(-π/4)- 24*(-π/4)+6π-3=-24+6π+6π-3=-31+12π
    y(0)=24*tg0°-24*0+6π-3=6π-3
    y(π/4)=24*tg(π/4)-24/(π/4)+6π-3=24-6π+6π-3=21
    ответ: наибольшее значение функции у(π/4)=21

1 2 3 > >>