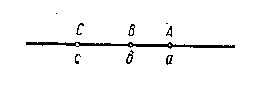Числовые неравенства

Если числа a и b равны между собой, то a - b = 0. Если же числа a и b не равны между собой, то разность a - b либо положительна, либо отрицательна.

Если разность a - b положительна, то говорят, что число a больше числа b; записывается это таким образом:

a > b. (1)

Если разность a - b отрицательна, то говорят, что число a меньше числа b; записывается это таким образом:

a < b. (2)

Например, 5 > 3, поскольку разность 5 - 3 = 2 положительна; - 7 < - 6, так как разность (- 7) - (- 6) = - 1 отрицательна.

Записи (1) и (2) называются числовыми неравенствами, а знаки > и <, участвующие в них, -знаками неравенства.

Числовые неравенства допускают простую геометрическую интерпретацию. Будем изображать числа точками числовой прямой. Пусть числу a соответствует точка А, а числу b - точка В. Тогда, если а > b, то точка А будет лежать правее точки В. Если же a < b, то точка А будет лежать левее точки В.

До сих пор мы говорили лишь о таких неравенствах, обе части которых представляют собой вполне определенные числа. (Правда, для общности рассуждений мы обозначали эти числа буквами.) Однако в математике часто приходится иметь дело и с такими неравенствами, отдельные члены которых, выраженные с помощью букв, могут принимать различные числовые значения, например,

\(\sqrt{a}\) > a, (3)

¹/_a > 3, (4)

a - 1 < a, (5)

\(\sqrt{a}\) + \(\sqrt{b}\) < 0,5. (6)

Допустимыми значениями букв, входящих в неравенство, называются такие значения этих букв, при которых обе части неравенства имеют смысл.

Очевидно, что допустимыми значениями a в неравенстве (3) служат все положительные числа и нуль, в неравенстве (4) - все числа, кроме нуля, в неравенстве (5) - все числа. Для неравенства (6) допустимые значения a и b складываются из всевозможных пар неотрицательных чисел.

Рассмотрим подробнее неравенство (3). Оно, как мы уже говорили, определено для всех неотрицательных значений a. Однако не каждое из указанных чисел удовлетворяет этому неравенству. Действительно, при a = 0,25 \(\sqrt{a}\) = 0,5. Поскольку 0,5 > 0,25, то число a = 0,25 удовлетворяет неравенству (3). А вот число 4 ему уже не удовлетворяет, поскольку \(\sqrt{4}\) < 4. Таким образом, неравенству, содержащему букву, могут удовлетворять одни допустимые значения этой буквы и не удовлетворять другие допустимые значения этой буквы.

Неравенство, которому удовлетворяют все допустимые значения входящих в него букв, называется тождественным неравенством.

Примером такого неравенства может служить хотя бы неравенство (5). При любом значении a a - 1 < a. Неравенство (4) нельзя отнести к тождественным неравенствам; ему не удовлетворяет, например, значение a = 1: ¹/₁ < 3.

Основные свойства числовых неравенств

1. Если a > b, то b < а, и, наоборот, если a < b, то b > а.

   Доказательство. Пусть a > b. По определению это означает, что число (a - b) положительно. Если мы перед ним поставим знак минус, то полученное число - (a - b) будет, очевидно, отрицательным. Поэтому - (a - b) < 0, или b - а < 0. А это (опять же по определению) и означает, что b < a.

   Обратное утверждение предлагаем учащимся доказать самостоятельно.

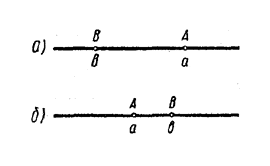
   Доказанное свойство неравенств допускает простую геометрическую интерпретацию: если точка А лежит на числовой прямой правее точки В, то точка В лежит левее точки А, и наоборот.

   

2. Если a > b, a b > c, то a > с.

   Геометрически это свойство состоит в следующем. Пусть точка А (соответствующая числу a) лежит правее точки В (соответствующей числу b), а точка В, в свою очередь, лежит правее точки С (соответствующей числу с). Тогда точка А и подавно будет лежать правее точки С.

   

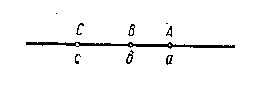
   Приведем алгебраическое доказательство этого свойства неравенств.

   Пусть a > b, a b > с. Это означает, что числа (a - b) и (b- с) положительны. Сумма двух положительных чисел, очевидно, положительна. Поэтому (a - b) + (b- с) > 0, или a - с > 0. Но это и означает, что a > с.

3. Если a > b, то для любого числа с a + с > b + с, a - c > b - с.

   Иными словами, если к обеим частям числового неравенства прибавить или от обеих частей отнять одно и то же число, то неравенство не нарушится.

   Доказательство. Пусть a > b. Это означает, что a - b > 0. Но a - b = (a + с) - (b + с). Поэтому (a + с) - (b + с) > 0. А по определению это и означает, что a + с > b + с. Аналогично показывается, что a - c > b - с.

   Например, если к обеим частям неравенства 5 > 4 прибавить 1¹/₂, то получим
   6¹/₂ > 5¹/₂. Отнимая от обеих частей данного неравенства число 5, получим 0 > - 1.

   Следствие. Любое слагаемое одной части числового неравенства можно перенести в другую часть неравенства, поменяв знак этого слагаемого на противоположный.

   Пусть, например, a + b > с. Требуется доказать, что a > с - b. Для доказательства от обеих частей данного неравенства достаточно отнять число b.

4. Пусть a > b. Если с > 0, то аc > bc. Если же с < 0, то ас < bс.

   Иными словами, если обе части числового неравенства умножить на положительное число, то неравенство не нарушится;
   если обе части неравенства умножить на отрицательное число, то знак неравенства изменится на противоположный.

   Короче это свойство формулируется таким образом:

   Неравенство сохраняется при почленном умножении на положительное число и изменяет знак на противоположный при почленном умножении на отрицательное число.

   Например, умножив неравенство 5 > 1 почленно на 7, получим 35 > 7. Почленное умножение того же неравенства на - 7 дает - 35 < - 7.

   Доказательство 4-го свойства.

   Пусть а > b. Это означает, что число а - b положительно. Произведение двух положительных чисел а - b и с, очевидно, также положительно, т. е. (a - b) с > 0, или
   aс - bс > 0. Поэтому aс > bс.

   Аналогично рассматривается случай, когда число с отрицательно. Произведение положительного числа a - b на отрицательное число с, очевидно, отрицательно, т. е.
   (а - b) с < 0; поэтому aс - bс < 0, откуда aс < bс.

   Следствие. Знак неравенства сохраняется при почленном делении на положительное число и изменяется на противоположный при почленном делении на отрицательное число.

   Это вытекает из того, что деление на число с =/= 0 равносильно умножению на число ¹/_c.

Сложение и вычитание неравенств

Про два неравенства, имеющие одинаковые знаки неравенства (оба знак > или оба знак < ), говорят, что они одинакового смысла. Например, неравенства a > b и 3 > 2 - одинакового смысла, так как оба они имеют один и тот же знак > ; неравенства a < b и, a < с также одинакового смысла, поскольку имеют один и тот же знак <.

Если одно из неравенств имеет знак >, а другое знак <, то такие неравенства называются неравенствами противоположного смысла. Например, 16 > 0 и 5 < a - неравенства противоположного смысла.

Теорема 1. Неравенства одинакового смысла можно почленно складывать.

Доказательство. Пусть a > b и с > d. Докажем, что a + с > b + d.

Так как a > b и с > d, то числа (a - b) и (с - d) положительны. Сумма двух положительных чисел также положительна: (a - b) + (с - d) > 0.

Но (a - b) + (с - d) = (a + с) - (b + d).

Поэтому число (a + с) - (b + d) положительно. А это и означает, что a + с > b + d.

Случай, когда складываются неравенства a < b и с < d, предлагаем учащимся рассмотреть самостоятельно.

Примеры:

$$ \frac{+\begin{cases}0 > -100\\65 > 64\end{cases}}{65 > -36} \;\;\;\; \frac{+\begin{cases}14 < 15\\-20 < -15\end{cases}}{-6 < 0} $$

Теорема 2. Два неравенства противоположного смысла можно почленно вычитать, оставляя знак того неравенства из которого мы вычитаем.

Например:

$$ \frac{-\begin{cases}2 > 0\\-3 < 6\end{cases}}{5 > -6} \;\;\;\; \frac{-\begin{cases}10 < 15\\3 > 2\end{cases}}{7 < 13} $$

Доказательство. Пусть a > b и с < d. Покажем, что a - c > b - d.

Почленное умножение неравенства c < d на - 1 дает - с > - d. Сложив это неравенство с данным неравенством a > b, получим a - c > b - d.

Случай, когда a < b и с > d, предлагаем учащимся рассмотреть самостоятельно.

Замечание. Неравенства одинакового смысла почленно вычитать, вообще говоря, нельзя. Например, если бы мы из неравенства 2 > 0 вычли почленно неравенство 0 > - 5, то пришли бы к противоречию: 2 больше 5.

Умножение неравенств

Теорема. Неравенства одинакового смысла с положительными частями можно почленно умножать.

Доказательство. Пусть a > b и с > d, причем числа a, b, с и d положительны. Докажем, что aс > bd.

Умножив неравенство a > b почленно на положительное число с, получим aс > bc. Умножив затем неравенство с > d почленно на положительное число b, получим bc > bd. Теперь имеем: aс > bc, a bc > bd. Но тогда по второму основному свойству неравенств (§ 10) должно быть aс > bd.

Аналогично может быть рассмотрен случай, когда a < b и c < d.

Примеры:

$$ \frac{\cdot \begin{cases}2 > 1\\6 > 4\end{cases}}{12 > 4} \;\;\;\; \frac{\cdot \begin{cases}5 > 3\\100 > 10\end{cases}}{500 > 30}\;\;\;\; \frac{\cdot \begin{cases}1 < 7\\9 < 10\end{cases}}{9 < 70} $$

Следствие 1. Если a > b, причем числа a и b положительны, то для любого натурального п

aⁿ > bⁿ.

Действительно, умножая почленно неравенство a > b само на себя, получим a² > b². Умножая затем почленно полученное неравенство на исходное неравенство a > b, получим a³ > b³ и т. д.

Следствие 2. Если числа a и b положительны и

aⁿ > bⁿ (1)

(п - натуральное число), то a > b.

Действительно, возможен один из трех случаев: a = b, a < b и a > b.
Если а = b, то аⁿ = bⁿ.
При a < b мы имели бы b > а, и потому по следствию 1 bⁿ > aⁿ . И то и другое противоречит неравенству (1).
Остается признать, что а > b.

Пример. Определить, какое число больше: \(\sqrt{5}\) + \(\sqrt{6}\) или \(\sqrt{3}\) + \(\sqrt{8}\).

Возвысим оба числа в квадрат:

(\(\sqrt{5}\) + \(\sqrt{6}\))² = 5 + 2\(\sqrt{30}\) + 6 = 11 + 2\(\sqrt{30}\) ;
(\(\sqrt{3}\) + \(\sqrt{8}\))² = 3 + 2\(\sqrt{24}\) + 8 = 11 + 2\(\sqrt{24}\)

Квадрат первого числа больше квадрата второго числа. Так как эти числа положительны, то по следствию 2

\(\sqrt{5}\) + \(\sqrt{6}\) > \(\sqrt{3}\) + \(\sqrt{8}\):

Двойные неравенства

Иногда приходится иметь дело с двойными неравенствами. Так называются неравенства вида

a’ < а < а".

По существу, эта формула объединяет в себе два неравенства: a’ < а и a < а". Этим и объясняется название «двойное неравенство».

Двойные, неравенства обладают всеми теми свойствами, о которых мы говорили в § 10-12, когда рассматривали обычные неравенства. Например, к каждой части двойного неравенства можно прибавить любое число k:

a’ + k < а + k < а" + k. (1)

Каждую часть двойного неравенства можно умножить на любое положительное число k:

ka’ < ka < ka". (2)

Каждую часть двойного неравенства можно умножить и на любое отрицательное число l, поменяв при этом знаки неравенства на противоположные:

la’ > la > la". (3)

Строгие и нестрогие неравенства

Когда хотят записать, что число a не меньше числа b (другими словами, a больше или равно b), то используют знак > и пишут a > b. Например, a² + 1 > 1, | х | > 0 и т. д.

Если нужно записать, что число a не больше числа b (другими словами, a меньше или равно b), то используют знак < и пишут a < b. Например, 1 < 1 + a², - | х | < 0 и т. д.

Соотношения a > b и a < b, так же как и соотношения a > b и a < b, называются неравенствами. Неравенства, содержащие знак > или знак < , называются строгими, а неравенства, содержащие знак > или знак <, - нестрогими. Например, неравенства π < 4 и 2π > 6 - строгие, а неравенства 17 > 17 и 3 < 4 - нестрогие.

Все выведенные выше свойства строгих числовых неравенств легко распространяются и на нестрогие неравенства.

Например, если a > b, то b < a; если a > b, то а + с > b +с и т. д.

Способы доказательства неравенств

Доказать неравенство, содержащее некоторые буквы, - это значит показать, что ему удовлетворяют любые допустимые или специально указанные значения этих букв.

Существуют различные способы доказательства неравенств. Проиллюстрируем некоторые из них на конкретных примерах.

Пример 1. Доказать, что любые положительные числа a и b удовлетворяют неравенству

$$ \frac{a + b}{2} \geq \sqrt{ab} \;\;\;\;(1) $$

причем знак равенства имеет место тогда и только тогда, когда a = b .

1-й способ. Рассмотрим разность

$$ \frac{a + b}{2} - \sqrt{ab} $$

Ее можно привести к виду:

$$ \frac{a + b}{2} - \sqrt{ab} = \frac{a+b-2\sqrt{ab}}{2}=\frac{(\sqrt{a} - \sqrt{b})^2}{2} $$

Но (\(\sqrt{a}\) - \(\sqrt{b}\))² > 0.

Поэтому \(\frac{a + b}{2} - \sqrt{ab} \geq 0 \). А это и означает, что \(\frac{a + b}{2} \geq \sqrt{ab}\).

Знак равенства в формуле (1) имеет место тогда и только тогда, когда \(\sqrt{a}\) - \(\sqrt{b}\) = 0, т. е при a = b.

2-й способ. Предположим, что данное неравенство верно. Тогда, умножив обе его части на 2, получим:

a + b > 2 \(\sqrt{ab}\).

Перенесем 2 \(\sqrt{ab}\) в левую часть:

a + b - 2 \(\sqrt{ab}\) > 0.

Наконец, перепишем полученное неравенство в виде

(\(\sqrt{a}\) - \(\sqrt{b}\))² > 0. (2)

Последнее неравенство, очевидно, верно для любых положительных чисел a и b, причем равенство в нем достигается тогда и только тогда, когда a = b. Таким образом, данное неравенство мы свели к очевидному неравенству. Теперь, производя все рассуждения в обратном порядке, мы докажем данное неравенство.

Для любых, положительных чисел a и b имеем:

(\(\sqrt{a}\) - \(\sqrt{b}\))² > 0,

или

a - 2 \(\sqrt{ab}\) + b > 0.

Знак равенства при этом имеет место тогда и только тогда, когда a = b. Перенося - 2\(\sqrt{ab}\) в правую часть, получаем a + b > 2\(\sqrt{ab}\), откуда \(\frac{a + b}{2} \geq \sqrt{ab}\).

Сразу трудно было догадаться, что при доказательстве неравенства (1) нужно исходить из очевидного неравенства (2). Вот почему предварительно нам пришлось сделать допущение, что неравенство (1) верно, и получить при этом допущении неравенство (2).

Пример 2. Доказать, что если произведение положительных чисел х и у равно 1, то (1 + x)(1 + у) > 4.

Доказательство. Полагая в только что доказанном неравенстве

$$ \frac{a + b}{2} \geq \sqrt{ab}$$

a = 1, b = х, получим \(\frac{1 + x}{2} \geq \sqrt{x}\) или 1 + х > 2\(\sqrt{x}\)

Аналогично показывается, что 1 + y > 2\(\sqrt{y}\). Почленное умножение полученных неравенств дает:

(1 + х)(1+у) > 2\(\sqrt{x}\) •2\(\sqrt{y}\),

или

(1 + х)(1+у) > 4\(\sqrt{xy}\).

Но по условию ху = 1. Поэтому

(1 + х)(1+у) > 4.