Точки в системе координат

Декартова система координат

Пусть в пространстве заданы две различные произвольные точки О и М, и пусть одна из них, например точка О, выбрана в качестве начальной. Тогда вектор \(\vec{OM}\) называется радиус-вектором точки М относительно точки О (рис.).

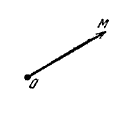
Пусть в пространстве задана точка О и некоторый базис e₁, e₂ , e₃. Совокупность этого базиса и точки О называется декартовой системой координат О, e₁, e₂ , e₃. Точка О называется началом координат.

Если через точку О провести прямые в направлениях, заданных базисными векторами e₁, e₂ и e₃, то полученные прямые называются осями координат (рис.);

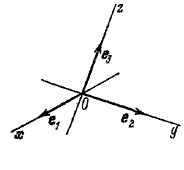
прямая Ох - осью абсцисс,
прямая Оу - осью ординат, а
прямая Oz - осью аппликат.

Координаты радиус-вектора точки М называются координатами этой точки в данной системе координат (х - абсцисса, у - ордината, z - аппликата).

Аналогично определяется и декартова система координат О, e₁, e₂ на плоскости (это произвольная фиксированная точка О и некоторый базис e₁, e₂ на плоскости) (рис.).

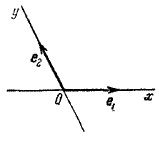
Координаты точки М записывают обычно рядом с буквой, ее обозначающей: М(х;у) на плоскости и М(х; у; z) в пространстве.

Очевидно, что декартова система координат в пространстве позволяет установить взаимно однозначное соответствие между точками пространства и упорядоченными тройками чисел, а на плоскости - взаимно однозначное соответствие между точками плоскости и упорядоченными парами чисел.

Например, точке А (рис.) соответствует упорядоченная пара чисел (2; 3); точке A₁ (рис.) -упорядоченная тройка чисел (2; -2; ¹/₂).

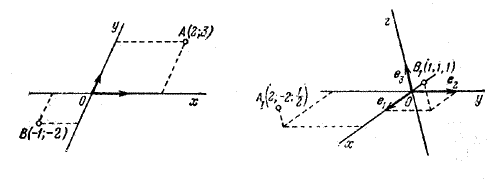
Упорядоченной паре чисел (-1; -2) соответствует единственная точка B плоскости (рис.), а упорядоченной тройке чисел (1;1;1) - единственная точка В₁ пространства (рис.).

Пусть в системе координат О, e₁, e₂ , e₃ задан некоторый вектор \(\vec{AB}\) (рис.).

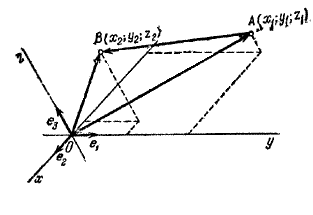
Тогда

\(\vec{AB}\) = \(\vec{OB}\) - \(\vec{OA}\).

Пусть координаты точек А и В соответственно равны (x₁; y₁; z₁) и (x₂; y₂; z₂). Тогда по свойству вычитания векторов, заданных своими координатами,

$$ \vec{AB} = (x_2 - x_1; y_2 - y_1; z_2 - z_1) $$

Итак, чтобы найти координаты некоторого вектора, достаточно из координат его конца вычесть одноименные координаты его начала.

Если векторы e₁, e₂ и e₃, составляющие базис, - попарно перпендикулярные единичные векторы, то система координат О, e₁, e₂ , e₃ называется прямоугольной декартовой системой координат в пространстве.

Аналогично, если единичные базисные векторы e₁ и e₂ взаимно перпендикулярны, то система координат О, e₁, e₂ называется прямоугольной декартовой системой координат на плоскости.

Единичные базисные векторы прямоугольной декартовой системы координат обозначают обычно буквами i , j и k.

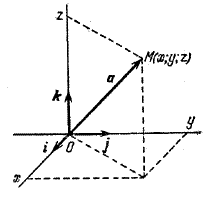
Разложение вектора \(а = \vec{OM}\) (рис.) пространства по векторам i , j , k записывают в виде

а = xi + yj + zk.

В этом случае говорят, что вектор а разложен по единичным векторам (ортам) в прямоугольном декартовом базисе пространства.

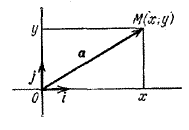
Разложение вектора а (рис.) по векторам i и j в прямоугольном декартовом базисе плоскости записывают в виде:

a = xi + yj

Такое разложение вектора всегда возможно и единственно.

Задача 2. Найти разложения векторов \(\vec{OM_1}\) и \(\vec{M_{1}N}\) в изображенном на рис. декартовом прямоугольном базисе (точка M₁ - проекция точки М на плоскость хОу).

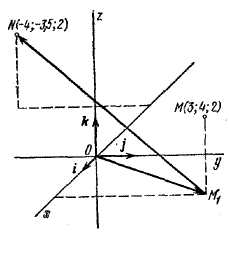
Так как точка M₁ есть проекция точки М на плоскость хОу, то M₁(3;4; 0). Поэтому

\(\vec{OM_1} = 3i + 4j + 0 \cdot k\).

Найдем теперь координаты вектора \(\vec{M_{1}N}\) в данном базисе: \(\vec{M_{1}N}\) = (- 4 - 3; - 3,5 - 4; 2 - 0), т. е. \(\vec{M_{1}N}\) = (-7; -7,5; 2). Следовательно, \(\vec{M_{1}N}\) = - 7i -7,5j + k.

Преобразование координат

Положение точки на плоскости определяется двумя координатами относительно некоторой системы координат. Координаты точки изменятся, если мы выберем другую систему координат.

Задача преобразования координат состоит в том, чтобы, зная координаты точки в одной системе координат, найти ее координаты в другой системе.

Эта задача будет разрешена, если мы установим формулы, связывающие координаты произвольной точки по двум системам, причем в коэффициенты этих формул войдут постоянные величины, определяющие взаимное положение систем.

Пусть даны две декартовы системы координат хОу и XO₁Y (рис.).

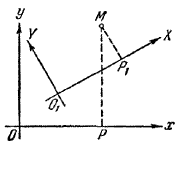
Положение новой системы XO₁Y относительно старой системы хОу будет определено, если известны координаты а и b нового начала O₁ по старой системе и угол α между осями Ох и О₁Х. Обозначим через х и у координаты произвольной точки М относительно старой системы, через X и Y-координаты той же точки относительно новой системы. Наша задача заключается в том, чтобы старые координаты х и у выразить через новые X и Y. В полученные формулы преобразования должны, очевидно, входить постоянные a, b и α.

Решение этой общей задачи мы получим из рассмотрения двух частных случаев.

1. Меняется начало координат, направления же осей остаются неизменными (α = 0).

2. Меняются направления осей, начало же координат остается неизменным (а = b = 0).

Перенос начала координат

Пусть даны две системы декартовых координат с разными началами O и O₁ и одинаковыми направлениями осей (рис.).

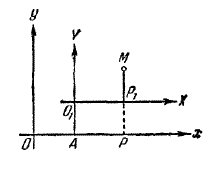
Обозначим через а и b координаты нового начала О₁ в старой системе и через х, у и X, Y-координаты произвольной точки М соответственно в старой и новой системах. Проектируя точку М на оси О₁Х и Ох, а также точку О₁ на ось Ох, получим на оси Ох три точки О, А и Р. Величины отрезков \(\overline{OA}\), \(\overline{AP}\) и \(\overline{OP}\) связаны следующим соотношением:

$$ |\overline{OA}| + |\overline{AP}| = |\overline{OP}| \;\;\; (1)$$

Заметив, что \(|\overline{OA}| = a\), \(|\overline{OP}| = x\), \(|\overline{AP}| = |\overline{O_1P_1}| = X\), перепишем равенство (1) в виде:

а + X = x или x = X + а. (2)

Аналогично, проектируя М и О₁ на ось ординат, получим:

y = Y + b (3)

Итак, старая координата равна новой плюс координата нового начала по старой системе.

Из формул (2) и (3) новые координаты можно выразить через старые:

Х = х - а, (2’)

Y = y - b. (3’)

Поворот осей координат

Пусть даны две декартовы системы координат с одинаковым началом О и разными направлениями осей (рис.).

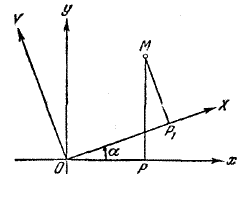
Пусть α - угол между осями Ох и ОХ. Обозначим через х, у и X, Y координаты произвольной точки М соответственно в старой и новой системах:

$$ x=|\overline{OP}|, \;\; y=|\overline{PM}| \\ X=|\overline{OP_1}|, \;\; Y=|\overline{P_1M}| $$

Рассмотрим ломаную линию \(\overline{OP_1MP}\) и возьмем ее проекцию на ось Ох. Замечая, что проекция ломаной линии равна проекции замыкающего отрезка, имеем:

$$ \overline{OP_1MP} = |\overline{OP}| \;\;\;(4)$$

С другой стороны, проекция ломаной линии равна сумме проекций ее звеньев; следовательно, равенство (4) запишется так:

$$ пр\overline{OP_1} + пр\overline{P_1M} + пр\overline{MP} = |\overline{OP}| \;\;\;(4’)$$

Так как проекция направленного отрезка равна его величине, умноженной на косинус угла между осью проекций и осью, на которой лежит отрезок, то

$$ пр\overline{OP_1} = Xcos\alpha \\ пр\overline{P_1M} = Ycos(90° +\alpha) = -Ysin\alpha \\ пр\overline{MP} = 0 $$

Отсюда равенство (4’) нам дает:

x = X cos α - Y sin α. (5)

Аналогично, проектируя ту же ломаную на ось Оу, получим выражение для у. В самом деле, имеем:

$$ пр\overline{OP_1} + пр\overline{P_1M} + пр\overline{MP} = пр\overline{OP} = 0 $$

Заметив, что

$$ пр\overline{OP_1} = Xcos(\alpha - 90°) = Xsin\alpha \\ пр\overline{P_1M} = Ycos\alpha \\ пр\overline{MP} = -y $$

будем иметь:

X sin α + Y cos α - y = 0,

или

y = X sin α + Y cos α. (6)

Из формул (5) и (6) мы получим новые координаты X и Y выраженными через старые х и у, если разрешим уравнения (5) и (6) относительно X и Y.

Замечание. Формулы (5) и (6) могут быть получены иначе.

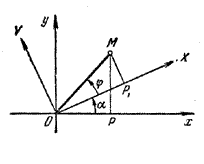
Из рис. имеем:

х = ОР = ОМ cos (α + φ) = ОМ cos α cos φ - ОМ sin α sin φ,

у = РМ = ОМ sin (α + φ) = ОМ sin α cos φ + ОМ cos α sin φ.

Так как OM cos φ = X, ОМ sin φ =Y, то

x = X cos α - Y sin α, (5)

y = X sin α + Y cos α. (6)

Общий случай

Пусть даны две декартовы системы координат с разными началами и разными направлениями осей (рис.).

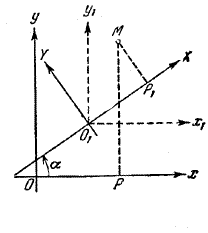
Обозначим через а и b координаты нового начала О, по старой системе, через α - угол поворота координатных осей и, наконец, через х, у и X, Y - координаты произвольной точки М соответственно по старой и новой системам.

Чтобы выразить х и у через X и Y, введем вспомогательную систему координат x₁O₁y₁, начало которой поместим в новом начале О₁, а направления осей возьмем совпадающими с направлениями старых осей. Пусть x₁ и y₁, обозначают координаты точки М относительно этой вспомогательной системы. Переходя от старой системы координат к вспомогательной, имеем:

х = х₁+ а, у = у₁ + b.

Переходя, далее, от вспомогательной системы координат к новой, найдем:

х₁ = X cos α - Y sin α, y₁ = X sin α + Y cos α.

Заменяя х₁ и y₁ в предыдущих формулах их выражениями из последних формул, найдем окончательно:

x = X cos α - Y sin α + a

y = X sin α + Y cos α + b

Полученные формулы содержат как частный случай формулы из предыдущих разделов. Так, при α = 0 данные формулы обращаются в

x = X + а, y = Y + b,

а при а = b = 0 имеем:

x = X cos α - Y sin α, y = X sin α + Y cos α.

Из приведенных формул мы получим новые координаты X и Y выраженными через старые х и у, если уравнения решим относительно X и Y.

Отметим весьма важное свойство указанных формул: они линейны относительно X и Y, т. е. вида:

x = AX + BY + C, y = A₁X + B₁Y + C₁.

Легко проверить, что новые координаты X и Y выразятся через старые х и у тоже формулами первой степени относительно х и у.