Переход от одной прямоугольной декартовой системы координат к другой

Выбором прямоугольной декартовой системы координат устанавливается взаимно однозначное соответствие между точками плоскости и упорядоченными парами действительных чисел. Это означает, что каждой точке плоскости соответствует единственная пара чисел и каждой упорядоченной паре действительных чисел соответствует единственная точка.

Выбор той или иной системы координат ничем не ограничен и определяется в каждом конкретном случае только соображениями удобства. Часто одно и то же множество приходится рассматривать в разных координатных системах. Одна и та же точка в разных системах имеет, очевидно, различные координаты. Множество точек (в частности, окружность, парабола, прямая) в разных системах координат задается различными уравнениями.

Выясним, как преобразуются координаты точек плоскости при переходе от одной координатной системы к другой.

Пусть на плоскости заданы две прямоугольные системы координат: О, i, j и О’, i’, j’.

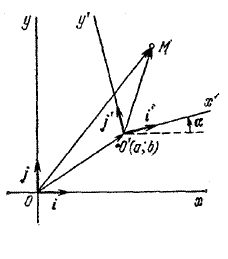
Первую систему с началом в точке О и базисными векторами i и j условимся называть старой, вторую - с началом в точке О’ и базисными векторами i’ и j’ - новой.

Положение новой системы относительно старой будем считать известным: пусть точка О’ в старой системе имеет координаты (a;b), a вектор i’ образует с вектором i угол α. Угол α отсчитываем в направлении, противоположном движению часовой стрелки.

Рассмотрим произвольную точку М. Обозначим ее координаты в старой системе через (х;у), в новой - через (х’у’). Наша задача - установить зависимость между старыми и новыми координатами точки М.

Соединим попарно точки О и О’, О’ и М, О и М. По правилу треугольника получаем

$$ \vec{OM} = \vec{OO’} + \vec{O’M} \;\;\;(1)$$

Разложим векторы \(\vec{OM}\) и \(\vec{OO’}\) по базисным векторам i и j, а вектор \(\vec{O’M}\) по базисным векторам i’ и j’:

$$ \vec{OM} = xi + yj, \;\;\vec{OO’} = ai + bj, \;\;\vec{O’M} = x’i’ + y’j’ $$

Теперь равенство (1) можно записать так:

xi + yj = (ai + bj) + ( x’i ’+ y’j ’ ). (2)

Новые базисные векторы i’ и j’ раскладываются по старым базисным векторам i и j следующим образом:

i’ = cos α i + sin α j,

j’ = cos (^π/₂ + α) i + sin ( ^π/₂ + α) j = - sin α i + cos α j.

Подставив найденные выражения для i’ и j’ в формулу (2), получим векторное равенство

xi + yj = ai + bj + х’(cos α i + sin α j) + у’ (- sin α i + cos α j)

равносильное двум числовым равенствам:

$$ \begin{cases}x=a+x’cos\alpha -y’sin\alpha\\y=b+x’sin\alpha +y’cos\alpha \end{cases} \;\;\;(3) $$

Формулы (3) дают искомые выражения для старых координат х и у точки через ее новые координаты х’ и у’. Для того чтобы найти выражения для новых координат через старые, достаточно решить систему уравнении (3) относительно неизвестных х’ и у’.

Итак, координаты точек при переносе начала координат в точку (а; b) и повороте осей на угол α преобразуются по формулам (3).

Если изменяется только начало координат, а направления осей остаются прежними, то, полагая в формулах (3) α = 0, получаем

$$ \begin{cases}x=a+x’\\y=b+y’\end{cases} \;\;\;(4) $$

Эти формулы кратко называют формулами переносa.

Если начало координат остается прежним, а оси поворачиваются на угол α, то, полагая в формулах (3) а = b = 0, получаем

$$ \begin{cases}x=x’cos\alpha - y’sin\alpha\\y=x’sin\alpha+y’cos\alpha\end{cases} \;\;\;(5) $$

Формулы (5) называют формулами поворота.

Задача 1. Пусть координаты нового начала в старой системе (2; 3), а координаты точки А в старой системе (4; -1). Найти координаты точки А в новой системе, если направления осей остаются прежними.

По формулам (4) имеем

$$ \begin{cases}4 = 2 + x’\\ -1=3+y’\end{cases} \Rightarrow \begin{cases}x’=2\\y’=-4\end{cases} $$

Ответ. A(2; -4)

Задача 2. Пусть координаты точки Р в старой системе (-2; 1), а в новой системе, направления осей которой те же самые, координаты этой точки (5; 3). Найти координаты нового начала в старой системе.

А По формулам (4) получаем

$$ \begin{cases} -2=a+5\\1=b+3\end{cases} $$

откуда а = - 7, b = - 2.

Ответ. (-7; -2).

Задача 3. Координаты точки А в новой системе (4; 2). Найти координаты этой точки в старой системе, если начало координат осталось прежним, а оси координат старой системы повернуты на угол α = 45°.

По формулам (5) находим

$$ \begin{cases}x=4cos45° - 2sin45°=4\cdot\frac{\sqrt2}{2}-2\cdot\frac{\sqrt2}{2}=\sqrt2\\y=4sin45°+2cos45°=4\cdot\frac{\sqrt2}{2}+2\cdot\frac{\sqrt2}{2}= 3\sqrt2\end{cases} $$

Ответ: \(A(\sqrt2; 3\sqrt2)\)

Задача 4. Координаты точки A в старой системе (2√3; -√3). Найти координаты этой точки в новой системе, если начало координат старой системы перенесено в точку (-1;-2), а оси повернуты на угол α = 30°.

По формулам (3) имеем

$$ \begin{cases}2\sqrt3= -1+x’cos30° - y’sin30°\\-\sqrt3= -2+x’sin30° + y’cos30°\end{cases} $$ $$ \begin{cases}2\sqrt3 = -1+x’\cdot\frac{\sqrt3}{2}-y’\cdot\frac{1}{2}\\-\sqrt3= -2+x’\cdot\frac{1}{2}+y’\cdot\frac{\sqrt3}{2}\end{cases} $$ $$ \begin{cases}\sqrt3x’ - y’=4\sqrt3+2\\x’+\sqrt3y’ = 4-2\sqrt3 \end{cases} $$

Решив эту систему уравнений относительно х’ и у’, найдем: х’ = 4, у’ = -2.

Ответ. A (4; -2).

Задача 5. Дано уравнение прямой у = 2х - 6. Найти уравнение той же прямой в новой системе координат, которая получена из старой системы поворотом осей на угол α = 45°.

Формулы поворота в данном случае имеют вид

$$ \begin{cases}x=x’cos45°-y’sin45° \\ y=x’sin45°+y’cos45° \end{cases} $$ $$ \begin{cases} x=\frac{\sqrt2}{2}x’ -\frac{\sqrt2}{2}y’=\frac{\sqrt2}{2}(x’-y’) \\ y=\frac{\sqrt2}{2}x’+\frac{\sqrt2}{2}y’= \frac{\sqrt2}{2}(x’+y’) \end{cases} $$

Заменив в уравнении прямой у = 2х - 6 старые переменные х и у новыми, получим уравнение

$$ \frac{\sqrt2}{2}(x’+y’) = 2\cdot \frac{\sqrt2}{2}(x’-y’)-6 $$

которое после упрощений принимает вид \(y’ = \frac{x’}{3} - 2\sqrt2\)