найдите корни уравнения, принадлежащие промежутку - страница 3
Найдите корни уравнения, принадлежащие промежутку [-π;π). Уравнение уже решено: КАК НАЙТИ КОРНИ ИМЕННО ЭТОГОПРОМЕЖУТКА?
cos(4x+π/4)=-корень из 2/2
4x+π/4=±(π-π/4)+2πn,n∈ℤ
4x=±3π/4-π/4+2πn,n∈ℤ
x=±3π/16-π/16+πn2,n∈ℤ
Решение: x = п/8 + пn/2Перебираем все целые числа n
если n=0, то x= п/8 (корень подходит)
если n=1, то x= 5п/8 (корень подходит)
если n=2, то x= 9п/8 (корень не подходит, потому что больше п), следовательно, все n, которые больше 2, не будут удовлетворять условию. Переходим на отрицательные.
если n=-1, то x= -3п/8 (корень подходит)
если n=-2, то x= -7п/8 (корень подходит)
если n=-3, то x= -11п/8 (корень не подходит, потому что меньше -п), следовательно, все n, которые меньше -3, не будут удовлетворять условию.
х = -п/4 + пn/2
Перебираем все целые числа n
если n=0, то x= -п/4 (корень подходит)
если n=1, то x= п/4 (корень подходит)
если n=2, то x= 3п/4 (корень подходит)
если n=3, то х= 5п/4 (корень не подходит, потому что больше п), следовательно, все n, которые больше 3, не будут удовлетворять условию. Переходим на отрицательные.
если n=-1, то x= -3п/4 (корень подходит)
если n=-2, то x= -5п/4 (корень не подходит, потому что меньше -п), следовательно, все n, которые меньше -2, не будут удовлетворять условию.
Найдите корни уравнение, принадлежащие промежутку [0;2pi] Указать наименьший корень.
Ответ указать в градусах.
Уравнение: $$ tgx*cosx+sinx*cosx=0 $$
Решение: $$ tgx*cosx+sinx*cosx=0 $$
$$ \frac{sinx}{cosx}*cosx+sinx*cosx=0 $$
$$ sinx+sinx*cosx=0 $$
$$ sinx*(1+cosx)=0 $$
1) $$ sinx=0 $$
$$ x= \pi k, k∈Z$$
2) $$ cosx=-1 $$
$$ x= \pi +2 \pi k, k∈Z$$
Выборка корней из [0; 2pi]:
C помощью единичной окружности (см. рисунок): 0, pi, 2pi
Наименьший из них: 0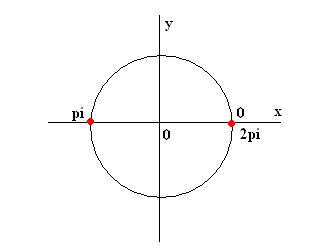
Найдите корни уравнения принадлежащие промежутку [0;2pi]
Укажите наибольший корень.
Ответ указать в градусах. (1 + cos x)(√2sin x - 1) = 0
Решение: 1) $$ cosx=-1 $$
$$ x= \pi +2 \pi k $$
2) $$ sinx= \frac{\sqrt{2}}{2} $$
$$ x= \frac{ \pi }{4}+2 \pi k $$
$$ x= \frac{5 \pi }{4}+2 \pi k $$
Выборка корней: pi/4, 5pi/4, pi
Наибольший из них: pi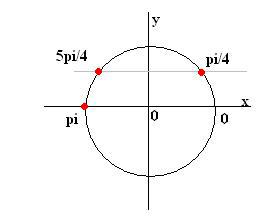
А) Решите уравнение. 2cos2x-4cosx-1=0
Б) Найдите все корни, принадлежащие промежутку {-5п/2; -п}
Решение: 2cos2x-4cosx-1=0
2(2cos²x-1)-4cosx-1=0
4cos²x-2-4cosx-1=0
4cos²x-4cosx -3=0
Пусть cosx=t; |t|≤1
4t²-4t-3=0
t=3/2- нет по ограничению на t
t=-½
cosx=-½
x=2π/3+2πk
x=-2π/3+2πk | k€Z
Б) (-2,5π;-π)
Выпишем первый набор корней:
x=2π/3+2πk
k=0: x= 2π/3
k=1: x= 8π/3
k=-1: x =-4π/3
k=-2: x= -10π/3
Выпишем второй набор корней:
x=-2π/3+2πk
k=0: x= -2π/3
k=-1: x= -8π/3
Ответ: А) { 2π/3+2πk; - 2π/3+2πk | k€Z}
Б) -4π/3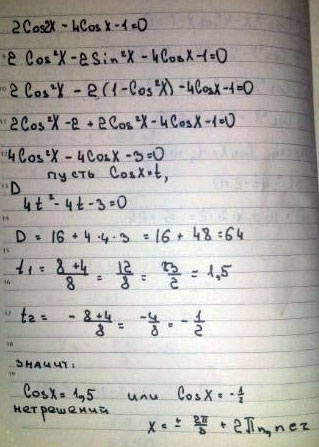
1)Решите уравнение: sin2x=cos(3п/2+x)
2) Найдите все корни, принадлежащие промежутку (4п/3; 4п]
Решение: Sin2x=cos(3п/2+x)
по формуле cos(3п/2+a)=-sina
cos(3п/2+x) =-sinx
sin2x=-sinx
2sinx*cosx=-sinx
разделим на sinx, при этом учитываем что корень уравнения sinx=0, тоже подходит
2cosx=-1
cosx=-1/2
x=arccos-1/2
x1=2п/3+2пn, n -целые числа и
x2=4п/3+2пn, n -целые числа
решая уравнение sinx=0, получаем, что x=пn, n -целые числа
из промежутка (4п/3 ; 4п] нам подходят 2п, 8п/3, 3п, 10п/3, 4п
ответ: 2п, 8п/3, 3п, 10п/3, 4п1)
$$ \sin2x=\cos(\frac{3\pi}{2}+x); \\ 2\sin x\cos x=\cos\frac{3\pi}{2}\cdot\cos x-\sin\frac{3\pi}{2}\cdot\sin x;\\ |\sin\frac{3\pi}{2}=-1;\\ \cos\frac{3\pi}{2}=0;| \\ 2\sin x\cos x=0\cdot\cos x-(-1)\cdot\sin x;\\2\sin x\cos x=\sin x; \\ 2\sin x\cos x-\sin x=0;\\sin x(2\cos x-1)=0;\\1) \sin x=0\ \\ \ x=\pi n, n\in Z;\\2) 2\cos x-1=0;\\2\cos x=1;\\\cos x=\frac12;\\x=\pm\arccos\frac12+2\pi k=\pm\frac\pi3+2\pi k. k\in Z\\ \left[ {{x=\pi n} \atop {x=\pm\frac\pi3+2\pi k}} \right.\ \\ \ n,k\in Z $$
2)
$$ x\in(\frac{4\pi}{3};4\pi]=(\pi+\frac{\pi}{3};4\pi] \\ 1) x=\pi n;\ \\ \=1:x=\piotin(\frac{4\pi}{3};4\pi];\=2:x=2\pi\in(\frac{4\pi}{3};4\pi];\=3:x=3\pi\in(\frac{4\pi}{3};4\pi];\=4:x\in(\frac{4\pi}{3};4\pi];\=5:xotin(\frac{4\pi}{3};4\pi];\ $$
$$ 2) x=\pm\frac{\pi}{3}+2\pi k;\\ k=0:x=\pm\frac\pi3otin(\frac{4\pi}{3};4\pi]; \\ k=1:x=\pm\frac{\pi}{3}+2\pi= \left[ {x=\frac{5\pi}{3}\in(\frac{4\pi}{3};4\pi];} \atop {x=\frac{7\pi}{3}\in(\frac{4\pi}{3};4\pi];} \right. \\k=2:x=\pm\frac\pi3+4\pi= \left[ {x=\frac{11\pi}{3}\in(\frac{4\pi}{3};4\pi]} \atop {x=\frac{13\pi}{3}otin(\frac{4\pi}{3};4\pi]} \right. $$
имеем такие ответы
$$ 2) x=\pm\frac{\pi}{3}+2\pi k; \\ k=0:x=\pm\frac\pi3otin(\frac{4\pi}{3};4\pi]; \\ k=1:x=\pm\frac{\pi}{3}+2\pi= \left[ {x=\frac{5\pi}{3}\in(\frac{4\pi}{3};4\pi];} \atop {x=\frac{7\pi}{3}\in(\frac{4\pi}{3};4\pi];} \right. \\ k=2:x=\pm\frac\pi3+4\pi= \left[ {{x=\frac{11\pi}{3}\in(\frac{4\pi}{3};4\pi]} \atop {x=\frac{13\pi}{3}otin(\frac{4\pi}{3};4\pi]}} \right. \\ x=\frac{5\pi}{3};2\pi; \frac{7\pi}{3}; 3\pi; \frac{11\pi}{3}; 4\pi $$