решение уравнений »

найдите корни уравнения, принадлежащие промежутку - страница 4

  • Решите уравнение 2sin^2(П/2-х) = -√3cosx
    Найдите его корни, принадлежащие промежутку -3П ; -3П/2


    Решение: 1) 2sin^2(П/2-x)=√3cosx;

    П/2 - следовательно, меняем sin на cos. Четверть I, значит, знак +.

    2cos^2x=√3cosx;

    Переносим:

    2cos^2x - √3cosx = 0;

    Выносим cos:

    cosx(2cosx -√3) = 0;

    Произведение равно нулю, когда один из множителей равен нулю, другой, при этом определен:

    cosx = 0 или 2cosx = √3;

    x=+-П/2 + 2ПK, K c Z. cosx = √3/2;

      x = +- П/6 +2Пn, n c Z;

    2) Не точно указали промежуток. Корни: -5П/2; -13П/6; -11П/6; Если дан отрезок - еще -3п/2. Если интервал - только те 3 корня.

  • Решите уравнение 3cosx + cos^2(3pi/2-x)=0 и найдите все корни, принадлежащие промежутку [-5pi/4;8pi/3]


    Решение: $$ 3cosx+2cos^{2}( \frac{3 \pi }{2}-x)=0 \\ 3cosx-2sin^{2}x=0 3cosx-2(1-cos^{2}x)=0 \\ 3cosx-2+2cos^{2}x=0 \\ 2cos^{2}+3cosx-2=0 \\ cosx=t \\ 2t^{2}+3t-2=0 \\ D=9+16=25 x_{1}=-3+5/4=1/2 \\ x_{2}=-3-5/4=-2 \\ cosx eq -2 \\ cosx=1/2 \\ x=-\pi/3+ 2\pi \\ x=\pi/3+ 2\pi \\ n=1 \\ x_{1}=-\pi /3+2 \pi=5 \pi /3 \\ x_{2}=\pi /3+2 \pi=7 \pi /3 \\ n=(-1) \\ x=\pi /3-2 \pi =-5 \pi /3 $$

    В общем этим отрезкам принадлежат 3 точки, указаны на графике.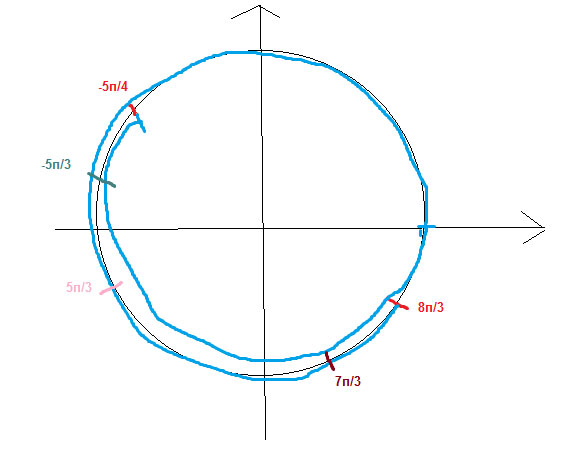 cosx cos frac pi -x cosx- sin x cosx- -cos x cosx- cos x cos cosx- cosx t t t- D x - x - - - cosx eq - cosx x - pi pi x pi pi n x - pi pi pi x pi pi pi n - x pi - pi - pi В о...

  • cos2x=sin(x+pi/2) Найдите корни этого уравнения,принадлежащие промежутку [-2pi;-pi]


    Решение:

    cos2x=cosx

    2cos^2x-1-cosx=0

    пусть cosx=t? -1<=t<=1

    2t^2-t-1=0

    D=1+8=9, d=3

    t=-1/2

    t=1

    cosx=-1/2 cosx=1

    x=+-pi/3+2pi*n, n принадлежит z x=2pi*n, n принадлежит z

    1. -2pi<=pi/3+2pi*n<=-pi (умножаем на 3)

      -6pi<=pi+6pi*n<=-3pi (переносим pi)

      -5pi<=6pi*n<=-4pi (делим на 6pi)

      -5/6<=n<=-4/6

    корней нет

    2. -2pi<=-pi/3+2pi*n<=-pi (умножаем на 3)

      -6pi<=-pi+6pi*n<=-3pi (переносим pi)

      -5pi<=6pi*n<=-2pi (делим на 6pi)

      -5/6<=n<=-2/6

      корней нет

    3. -2pi<=2pi*n<=-pi (делим на 2pi)

      -1<=n<=-1/2

    n=-1, корень: -2pi

    n=0, корень 0

  • По данному значению одной из тригонометрических функций и промежутку, которому принадлежит альфа, найдите значения остальных трёх основных тригонометрических функций: в) тангенс альфа=1/2, П < альфа < 3П/2
    б) катангенс альфа = -3,3П/2 < альфа < 2П


    Решение: 1) tgα=1/2, π<α<3π/2
    tgα=1/ctgα
    ctgα=2
    1+tg²α=1/cos²α
    cosα=1/√1+tg²α
    cosα=-1/√1+(1/2)²=-1/√1+1/4=-1/√5/4=-2√5/5
    sinα=√1-cos²α
    sinα=-√1-(-2√5/5)²=-√5/5
    Ответ: sinα=-√5/5, cosα=-2√5/5, ctgα=2.
    2) ctgα=-3, 3π/2<α<2π
    tgα=1/(-3)=-1/3
    cosα=1/√1+(1/3)²=3√10/10
    sinα=-√1-(3√10/10)²=-√10/10
    Ответ: sinα=-√19/10, cosα=9/10, tgα=-1/3.

    1)tga=1/2
    cos²a=1:(1+tg²a)=1:(1+1/4)=1:5/4=4/5
    cosa=-2/√5=-2√5/5
    sina=-√1-4/5=-1/√5=-√5/5
    ctga=1/tga=2
    2)ctga=-3
    sin²a=1:(1+ctg²a)=1:(1+9)=1/10
    sina=-√10/10
    cosa=√1-1/10=3/√10=3√10/10
    tga=1/ctga=-1/3

  • Определите число корней уравнения, принадлежащие промежутку [0;2π], используя график функции y=cosx.


    Решение: В левой части стоит просто cos(2x)

    $$ \cos2x=\dfrac15\\2\cos^2x-1=\dfrac15\\\cos^2x=\dfrac35\\\cos x=\pm\dfrac{\sqrt{15}}5 $$

    Cмотрим на рисунок - видим 4 корня.

<< < 234