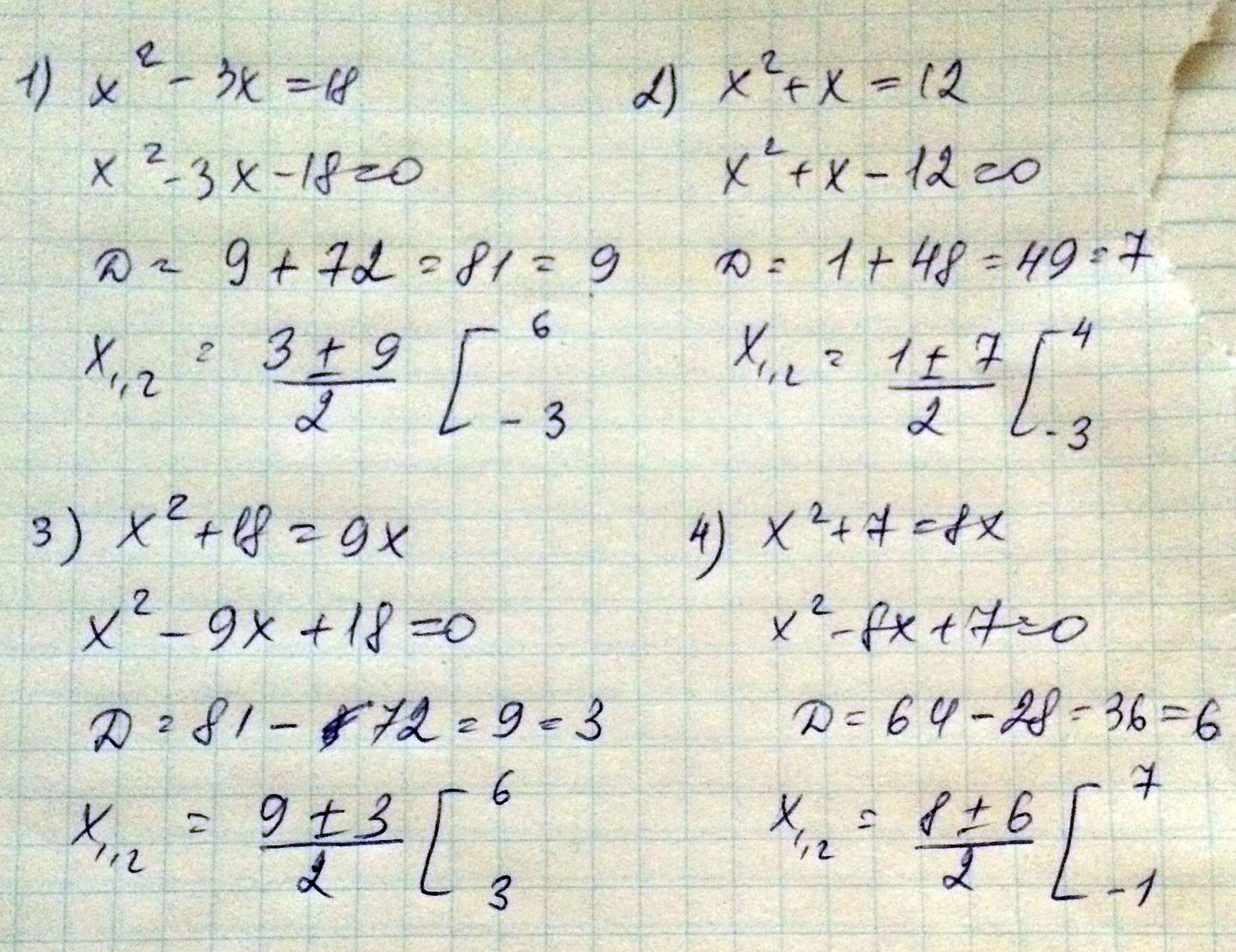решить квадратное уравнение через дискриминант - страница 3
Решить квадратные уравнения (с дискриминантом)1)3x^2+x-1=0 3x^2 это три в второй степени
2)5x^2-x-1=0
3) x/2 + 1/x = 4 x/2 - это дробь
Решение: 1-ое уравнение:
3x^2+x-1=0
D = 1^2 + 12 = 13
x1 = (-1 + √13) / 6
x2 = (-1 - √13) / 6
2-ое уравнение:
5x^2-x-1=0
D = 1^2 + 20 = 21
x1 = (1 + √21) / 10
x2 = (1 - √21) / 10
3-е уравнение:
x/2 + 1/x = 4
Умножим обе части уравнения на 2:
x + 2/x = 8
Умножим обе части на x не равный нулю:
x^2 + 2 = 8x
Перенесем всё в одну часть:
x^2 - 8x + 2 = 0
D = (-8)^2 - 8 = 56
x1 = (8 + √56) / 2
x1 = (8 - √56) / 2Как решать квадратные уравнения с дискриминантом?
Решение: Квадратное уравнение: ax^2+bx+c=0 (пример)
Дискриминант находится по формуле b^2-4ac
Если дискриминант меньше нуля, то действительных корней нет.
Если дискриминант равен нулю, то корень всего один.
Дальше находим корни (в квадратном уравнении их всего два).
Первый корень x1= (-b + квадратный корень из дискриминанта)/2a
Второй корень x2= (-b - квадратный корень из дискриминанта)/2aКаждое квадратное уравнение имеет вид $$ ax^2+bx+c=0 (a eq 0) $$
где a,b,c - какие либо числа, выражения.
формула дискриминанта имеет вид
$$ D=b^2-4ac $$
туда подставляем известные из уравнения нам значения a,b,c
Если D<0, то действительных решений нет. Для D=0 можно использовать формулу поиска корня $$ x= \frac{-b}{2a} $$
Для D>0 ищем корни по следующим формулам:
$$ x_1= \frac{-b+ \sqrt{D} }{2a} \\ x_2= \frac{-b- \sqrt{D} }{2a} $$Квадратные уравнения решить через дискриминант: x^2 - 3x = 18; x^2 + x = 12; x^2 + 18 = 9x; x^2 + 7 = 8x.
Решение: 1) Выражение: x^2-3*x-18=0
Квадратное уравнение, решаем относительно x: Ищем дискриминант:
D=(-3)^2-4*1*(-18)=9-4*(-18)=9-(-4*18)=9-(-72)=9+72=81;Дискриминант больше 0, уравнение имеет 2 корня:
x_1=(√81-(-3))/(2*1)=(9-(-3))/2=(9+3)/2=12/2=6;x_2=(-√81-(-3))/(2*1)=(-9-(-3))/2=(-9+3)/2=-6/2=-3.
2) Выражение: x^2+x-12=0.
Квадратное уравнение, решаем относительно x: Ищем дискриминант:
D=1^2-4*1*(-12)=1-4*(-12)=1-(-4*12)=1-(-48)=1+48=49;Дискриминант больше 0, уравнение имеет 2 корня:
x_1=(√49-1)/(2*1)=(7-1)/2=6/2=3;x_2=(-√49-1)/(2*1)=(-7-1)/2=-8/2=-4.
3) Выражение: x^2-9*x+18=0.
Квадратное уравнение, решаем относительно x: Ищем дискриминант:
D=(-9)^2-4*1*18=81-4*18=81-72=9;Дискриминант больше 0, уравнение имеет 2 корня:
x_1=(√9-(-9))/(2*1)=(3-(-9))/2=(3+9)/2=12/2=6;x_2=(-√9-(-9))/(2*1)=(-3-(-9))/2=(-3+9)/2=6/2=3.
4) Выражение: x^2-8*x+7=0.
Квадратное уравнение, решаем относительно x: Ищем дискриминант:
D=(-8)^2-4*1*7=64-4*7=64-28=36;Дискриминант больше 0, уравнение имеет 2 корня:
x_1=(√36-(-8))/(2*1)=(6-(-8))/2=(6+8)/2=14/2=7;x_2=(-√36-(-8))/(2*1)=(-6-(-8))/2=(-6+8)/2=2/2=1.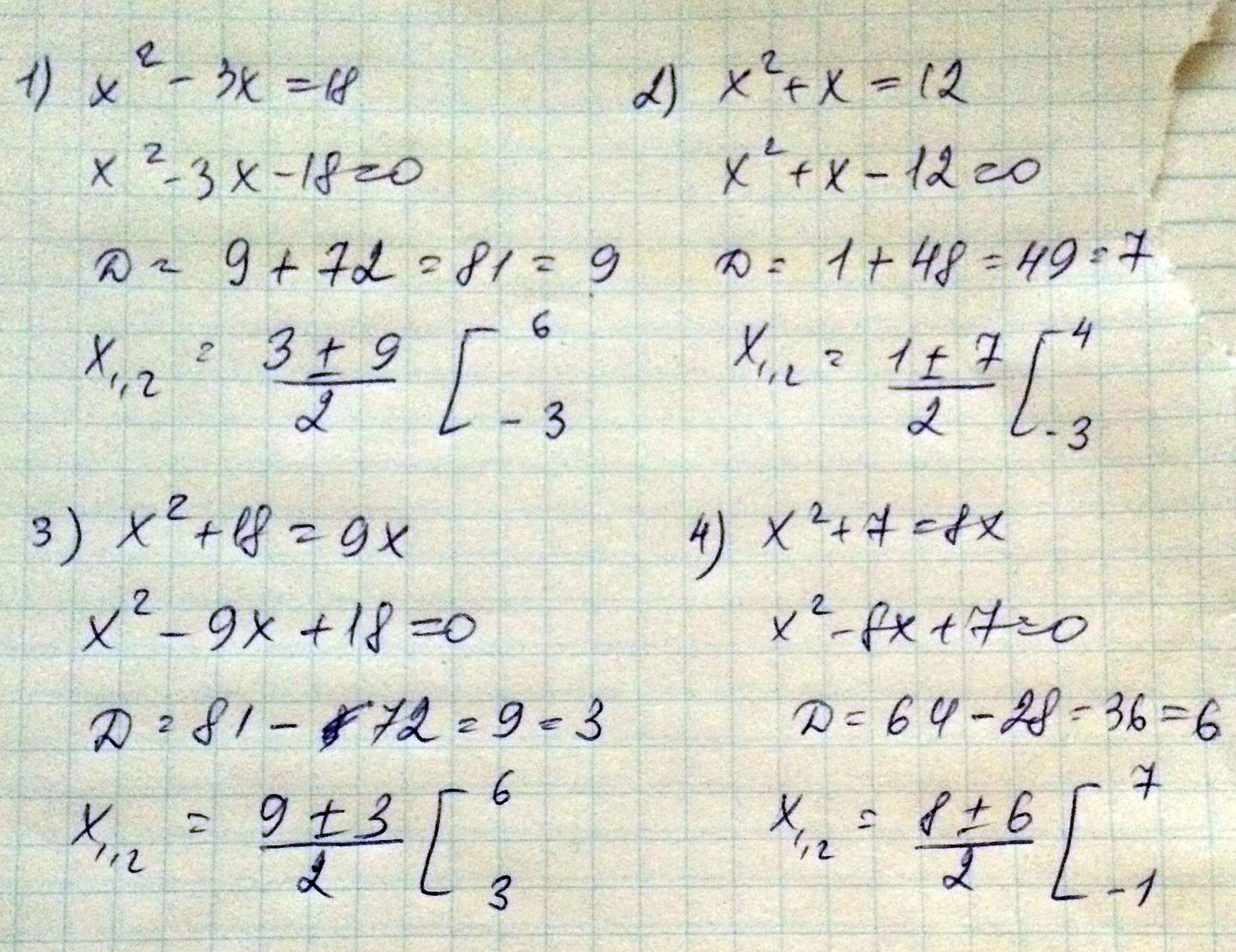
Решить квадратное уравнение через дискриминант: 15х²+7х-2=0 5х²-3х=0 4х²-9=0
Решение:$$ 15x^{2}+7x-2=0 $$
Cчитаем дискриминант:
$$ D=7^{2}-4\cdot15\cdot(-2)=49+120=169 $$
Дискриминант положительный
$$ \sqrt{D}=13 $$
Уравнение имеет два различных корня:
$$ x_{1}=\frac{-7+13}{2\cdot15}=\frac{6}{30}=\frac{1}{5}=0,2 $$
$$ x_{2}=\frac{-7-13}{2\cdot15}=\frac{-20}{30}=-\frac{2}{3} $$
================================================
$$ 5x^{2}-3x=0 $$
$$ x(5x-3)=0 $$
$$ x_{1}=0 $$
$$ 5x-3=0 $$
$$ 5x=3$$
$$x=3:5$$/p>
$$ x_{2}=\frac{3}{5} $$
===============================================
$$ 4x^{2}-9=0 $$
$$ 4x^{2}=9 $$
$$ x^{2}=9:4 $$
$$ x=\pm\sqrt{\frac{9}{4}}=\pm\sqrt{2,25} $$
$$ x_{1}=1,5 $$
$$ x_{2}=-1,5 $$
Решите квадратное уравнение, чере Дискриминант 1. 2х²+7х-4=0 2. 3х²-х-2=0 3. 9х²+6х+1=0 4.-4х²+12х-9=0
Решение: 1.2х²+7х-4=0D=b²-4*a*c
D=7²-4*2*(-4)=49-32=17
a1=-7-17= -24=-6 a2=-7+17= 10= 2,5
4 4 4 4
Ответ: -6; 2,5
2. 3х²-х-2=0
D=b²-4*a*c
D=(-1)-4*3*(-2)=1+24=25; 5
a1= 1-5=4=0,6 a2= 1+5=1
6 6 6
Ответ: 0,6; 1
3. 9х²+6х+1=0
D=b²-4*a*c
D=6²-4*9*1=36-36=0
уранение не имеет решения, т.к y>0 должно быть
4. -4х²+12х-9=0
D=b²-4*a*c
D=12²-4*(-4)*(-9)=144-144=0
уранение не имеет решения, т.к y>0 должно быть