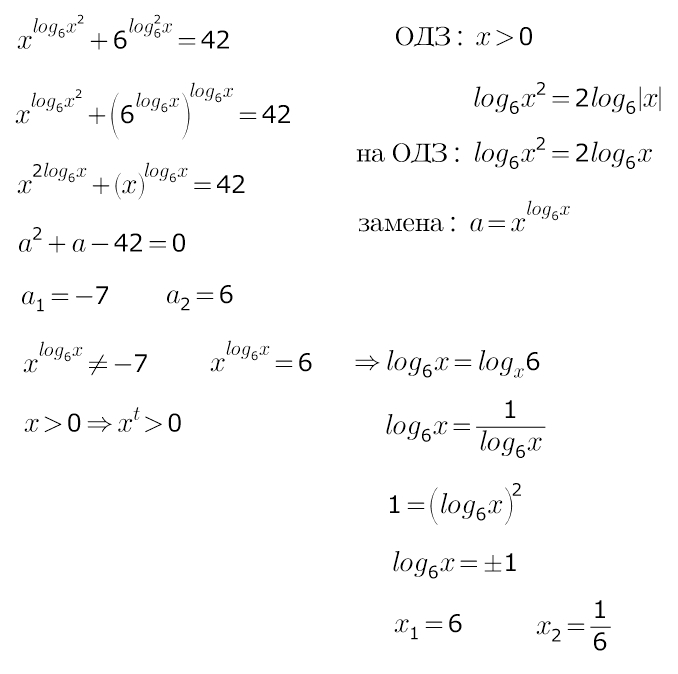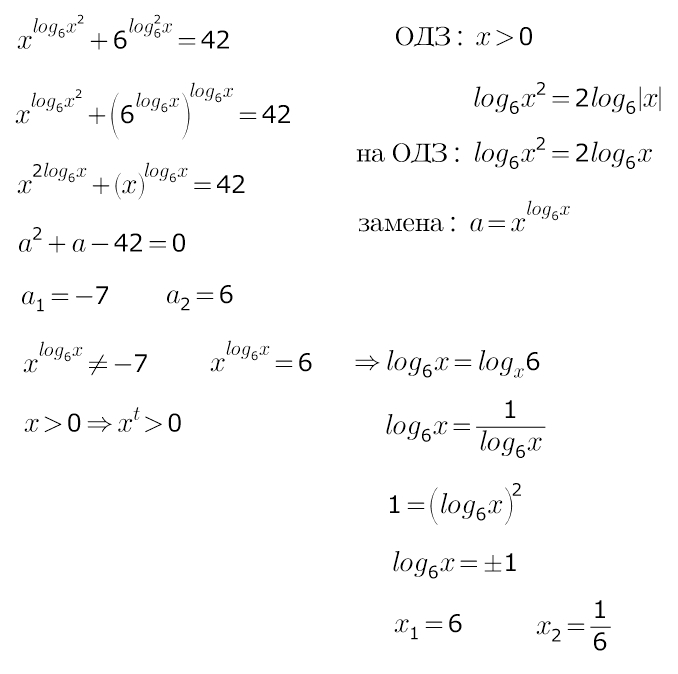решение уравнений »

решить логарифмическое уравнение - страница 6

  • Решить логарифмическое уравнение
    log0.8 ( 3x^2 + x + 4 ) = log0.8 ( 17x+1 )
    log4 ( x-4 ) +log4 ( x+4 ) = log4 ( 3x+2)
    log3 (3x+5) + log3 (2x-5) = log3 ( 10x -16)


    Решение: Log0.8 ( 3x^2 + x + 4 ) = log0.8 ( 17x+1 )
    {17x+1>0⇒x>-1/17
    {3x²+x+4>0⇒x∈R,
    D=1-48=-47<0
    x∈(-1/17;∞)
    3x²+x+4=17x+1
    3x²-16x+3=0
    D=256-36=220
    x1=(16-2√55)/6 U x2=(16+2√55(/2
    log4 ( x-4 ) +log4 ( x+4 ) = log4 ( 3x+2)
    {x-4>0⇒x>4
    x+4>0⇒x>-4
    {3x+2>0⇒x>-2/3
    x∈(4;∞)
    log(3)(x²-16)=log(4)(3x+2)
    x²-16=3x+2
    x²-3x-18=0
    x1+x2=3 u x1*x2=-18
    x1=-3 не удов усл
    х2=6
    log3 (3x+5) + log3 (2x-5) = log3 ( 10x -16)
    {3x+5>0⇒x>-5/3
    {2x-5>0⇒x>2,5
    {10x-16>0⇒x>1,6
    x∈(2,5;∞)
    log(3)[(3x+5)(2x-5)]=log(3)(10x-16)
    6x²-15x+10x-25=10x-16
    6x²-15x-9=0
    2x²-5x-3=0
    D=25+24=49
    x1=(5-7)/4=-0,5 не удов усл
    х2=(5+7)/4=3

  • Решить логарифмическое уравнение. \(\log_{x+20}(2x-\sqrt{x+20})=\frac{1}{2}\)


    Решение: 2x-√(x+20)=√(x+20), x=√(x+20), x²=x+20, x²-x-20=0, D=(-1)²-4*1*(-20)=81=9²,
    x1=(1+9)/2=5, x2=(1-9)/2=-4.
    Корень x=-4 не подходит, так как при этом выражение под знаком логарифма отрицательно (равно -12). А по определению логарифма, выражение под знаком логарифма должно быть положительным.
    Ответ: x=5

  • Решить логарифмическое уравнение, :
    lg\( \frac{3x-2}{3-4x} =0 \)


    Решение: ОДЗ:
    $$ \frac{3x-2}{3-4x}\ > \ 0 \\ \\ (3x-2)(3-4x)\ > \ 0 \\ 3(x- \frac{2}{3} )*(-4)(x- \frac{3}{4} )\ > \ 0 \\ (x- \frac{2}{3} )(x- \frac{3}{4} )\ < \ 0 \\ x= \frac{2}{3};x= \frac{3}{4} $$
      + - +
    - 2/3 - 3/4 -
      \\\\\\\\\\\\\
    x∈(2/3; 3/4)
    $$ \frac{3x-2}{3-4x}=10^0 \\ \\ \frac{3x-2}{3-4x}=1 \\ \\ 3x-2=3-4x \\ \\ 3x+4x=3+2 \\ 7x=5 \\ x= \frac{5}{7} $$
    5/7∈ОДЗ.
    Ответ: 5/7.

  • Решить логарифмическое уравнение \(x^{\log_6x^2} +6^{\log_6^2x}=42\)


    Решение: Все сведется к квадратному уравнению, которое решается по т. Виета)))
    и потом можно записать решение по определению логарифма.
    а можно прологарифмировать обе части равенства по основанию 6.

    X^(Log6 x²) +6^(Log6 x)² =42 ;
    ОДЗ : x >0
    x^(2Log6 x) +(6^Log6 x)^ (Log6 x) =42 ;
    (x^(Log6 x))² +x^(Log6 x) -42 =0 ; * * * t =x^(Log6 x) >0 * * *
    [x^ Log6 x = -7 ; x^ Log6 x  =6.
    x^ Log6 x  =6
    (Log6 x)² =1 ⇔[ Log6 x= -1 ; Log6 x =1⇔ [ x =1/6, x=6.

    Все сведется к квадратному уравнению которое решается по т. Виета и потом можно записать решение по определению логарифма.а можно прологарифмировать обе части равенства по ос...
<< < 456