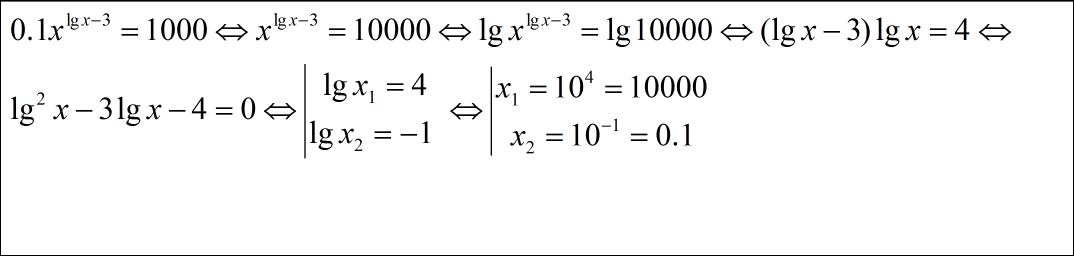решение уравнений »

решить логарифмическое уравнение - страница 4

  • Решить логарифмическое уравнение
    0,1x^(lgx-3)=1000


    Решение: 0,1x^(lgx-3)=1000
    x^(lgx-3)=10000
    (lgx-3)*lgx=4-логарифмируем.
    (lgx)^2-3lgx-4=0
    t^2-3t-4=0
    t1= -1=lgx->x1=0.1
    t2=4=lgx->x2=10000

    0,1x^(lgx-3)=1000-см.

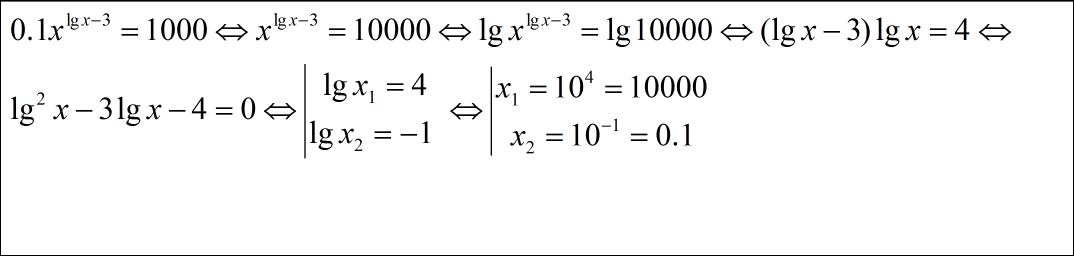
    x lgx- x lgx- lgx- lgx -логарифмируем. lgx - lgx- t - t- t - lgx- gt x . t lgx- gt x x lgx- -см....

  • Решить логарифмическое уравнение: \( log_{\frac{1}{\sqrt2}}\frac{1}{x^2-3x}=4 \)


    Решение: $$ log_{\frac{1}{\sqrt2}}\frac{1}{x^2-3x}=4\\-\\x^2-3x> 0\\x(x-3) > 0\\x=0;\ x=3\\x\in(-\infty;\ 0)\ \cup\ (3;\ \infty)\\- \\ log_{\frac{1}{\sqrt2}}\frac{1}{x^2-3x}=log_{\frac{1}{\sqrt2}}\left(\frac{1}{\sqrt2}\right)^4\iff\frac{1}{x^2-3x}=\frac{1}{4}\\\\x^2-3x=4\\\\x^2-3x-4=0\\\\\Delta=(-3)^2-4\cdot1\cdot4=9+16=25;\ \sqrt\Delta=\sqrt{25}=5\\\\x_1=\frac{3-5}{2\cdot1}=\frac{-2}{2}=-1;\ x_2=\frac{3+5}{2\cdot1}=\frac{8}{2}=4\\\\O:x=-1\ \vee\ x=4 $$

    log frac sqrt frac x - x - x - x x x- x x x in - infty cup infty - log frac sqrt frac x - x log frac sqrt left frac sqrt right iff frac x - x frac x - x x - x- Delta - - cdot...

  • РЕШИТЬ ЛОГАРИФМИЧЕСКОЕ УРАВНЕНИЕ \( log^{2} _{4} x-2 log_{4} x-3=0 \)


    Решение: $$ log^{2} _{4} x-2 log_{4} x-3=0 $$
    О. Д. З x>0
    Замена:$$ log_{4} x=t \\ t^{2} -2t-3=0 \\ D=4+12=16= 4^{2} \\ t_{1} = \frac{2+4}{2} = \frac{6}{2} =3 \\ t_{2} = \frac{2-4}{2} = \frac{-2}{2} =-1 \\ log_{4} x=-1 $$ и $$ log_{4} x=3 \\ x= \frac{1}{4} $$ $$ x=64 $$
    Ответ: $$ \frac{1}{4},64 $$

  • Решить логарифмическое уравнение \( \lg\sqrt{x-5} +\lg\sqrt{2x-3}+1 =\lg30 \)


    Решение: Вначале напишем ОДЗ
    х>5; х>3/2 по закону больше большего, общее ОДЗ х>5
    Складываем первых два логарифма, а единицу перебрасываем вправо получаем
    Lg(sqrt(x-5)*(2x-3))=lg30-lg10
    Lg(sqrt(x-5)*(2x-3))=lg3
    Sqrt((x-5)*(2x-3))=3
    Возводим обе части в квадрат и Раскрываем скобки
    2x^2-3x-10x+15-9=0
    2x^2-13x+6=0
    X=6
    X=1/2 не подходит по ОДЗ
    ОТВЕТ 6

  • Решить логарифмическое уравнение \(\log_3(\frac{x}{3})^2 +\log_3^2(\frac{x}{9})=5\)


    Решение: $$ log_3(\frac x3)^2+log_3^2(\frac x9)=5 \\ \\ \frac x3>0 \\ x>0 \\ \\ log_3(\frac {x^2}{9})+log_3^2(\frac x9)=5 \\ \\ log_3x^2-log_39+(log_3x-log_39)^2=5 \\ \\ log_3x^2-2-5+(log_3x-2)^2=0 \\ \\ 2log_3x-7+log_3^2x-2*2log_3x+4=0 \\ \\ log_3^2x-2log_3x-3=0 \\ \\ log_3x=t \\ \\ t^2-2t-3=0 \\ \\ t_1=3\ \ \ \ \ \ \ \ t_2=-1 \\ \\ log_3x=3 \\ \\ x_1=3^3=27 \\ \\ log_3x=-1 \\ \\ x_2=3^{-1}=\frac 13 $$

    Ответ: 27; 1/3

    ОДЗ: x>0

    Преобразуем

    log₃x² - log₃9+(log₃x - log₃9)²=5

    2log₃x - 2 + (log₃x - 2)²=5

    2log₃x - 2 + log²₃x - 4log₃x + 4 = 5

     log²₃x - 2log₃x - 3 = 0

     log₃x = - 1 или  log₃x = 3

    х=⅓ или х=27

    Ответ ⅓; 27.

<< < 234 5 6 > >>