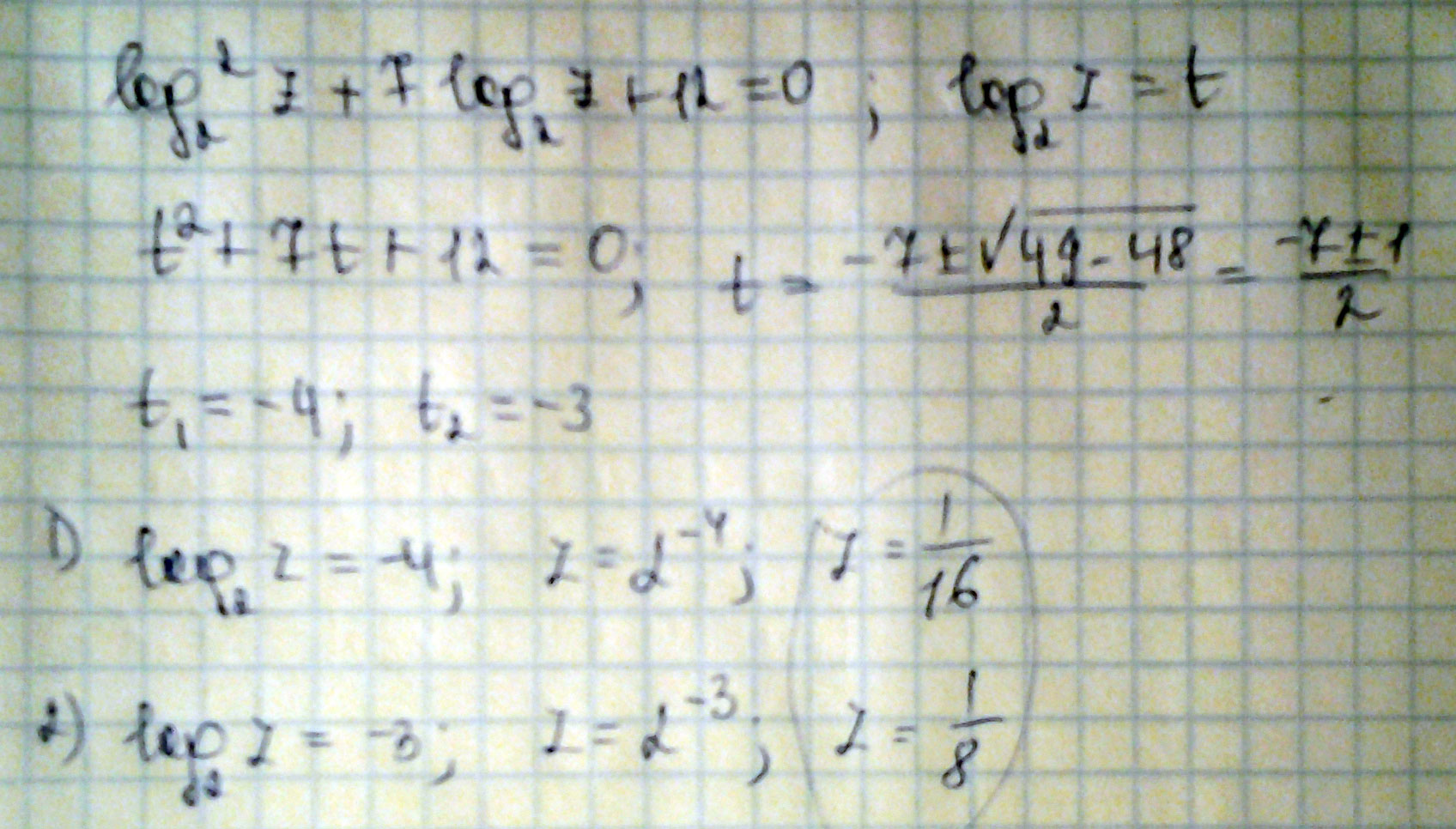решение уравнений »

решить логарифмическое уравнение - страница 5

  • Нужно решить логарифмическое уравнение \(\log^2_2 z - \log_2 z^{-7} +12=0 \)


    Решение: Log^2_2 z -Log_2 z^-7 +12=0
    Log2 z=t
    t^2 +7t+12=0
    t1= -4. t2= -3
    Log2 z= -4. Z=2^-4
    Z= 1/2^4=1/16
    -
    Log2 z= -3. Z=2^-3
    Z=1/2^3=1/8
    -
    Применены свойства логарифмов, замена переменной. Так ОДЗ: z> 0, то подходят оба корня.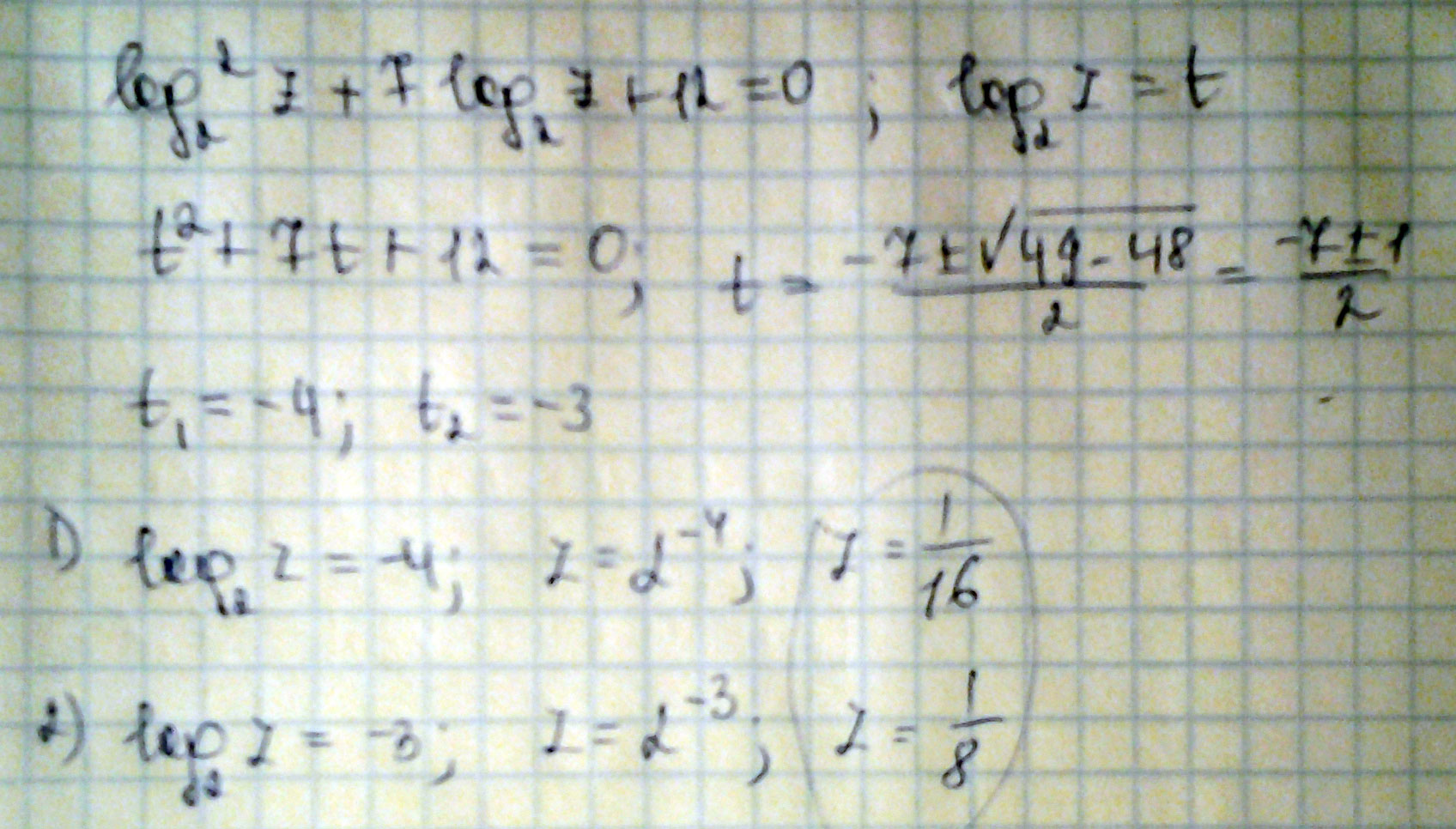

    Log z -Log z - Log z tt t t - . t - Log z - . Z - Z -Log z - . Z - Z -Применены свойства логарифмов замена переменной. Так ОДЗ z то подходят оба корня....

  • Решить логарифмическое уравнение \(\log_2(2x-1) +\log_2(x+5)=\log_2 13\)


    Решение: 1. Обязательно находите ОДЗ. Значение в логарифме всегда больше нуля. Другими словами 2x-1>0=> x>1/2, x+5>0=> x>-5. По свойству сложения логарифмов log2((2x-1)(x+5))=log2 13. Убираем логарифмы и получаем (2x-1)(x+5)=13. Раскрываете скобки, решаете квадратное уравнение, получаете ответ, сверяете с ОДЗ, все. Это лучше сделать самостоятельно.

    Log2(2x-1) +log2(x+5)=log2 13;
    найдём область допустимых значений:
    2х-1 >0, х>1/2, х>0,5;
    х+5>0, х>-5;
    одз: х>0,5
    log2 (2x-1)(x+5)=log2 13;
    (2х-1)(х+5)=13;
    2х^2-х+10х-5-13=0;
    2х^2+9х-18=0; делим на 2;
    х^2+9/2х-9=0;
    х^2+2*9/4х+81/16-81/16-9=0;
    (х+9/4)^2=81/16+144/16;
    (х+9/4)^2=225/16; извлекаем корень ;
    х+9/4=+-15/4;
    х1=-9/4-15/4=-24/4=-6; х2=-9/4+15/4=6/4=1,5;
    х1 не входит в Одз;
    Ответ: х=1,5.

  • Решить логарифмическое уравнение log_2(x-5)+log_2(x+2)=3


    Решение: ОДЗ:
    $$ \left \{ {{x-5\ > \ 0} \atop {x+2\ > \ 0}} \right. \ \ \ < \ =\ > \ \ \ \left \{ {{x\ > \ 5} \atop {x\ > \ -2}} \right. \ \ \ < \ =\ > \ \ \ x\ > \ 5 \\ log_2(x-5)+log_2(x+2)=3 \\ \\ log_2((x-5)(x+2))=3 \\ \\ (x-5)(x+2)=2^3 \\ \\ x^2+2x-5x-10=8 \\ \\ x^2-3x-18=0 \\ \\ x=6 \\ \\ x=-3 $$ - не удовлетворяет ОДЗ
    ОТВЕТ: 6

    Log2((x-5)*(x+2))=log2(8)
    (x-5)*(x+2)=8
    x^2-3x-10=8
    x^2-3x+2,25=20,25
    (x-1,5)^2=4,5^2
    x=6,  второе решение  x=-3 не годится, так как аргументы  логарифмов станут  отрицательны.
    Ответ: х=6

  • Решить логарифмическое уравнение \(\log_3\sqrt{x-5} +\log_3\sqrt{2x-3}=1\)


    Решение: Cумма логарифмов равна логарифму произведения, поэтому уравнение превращается в систему из уравнения и двух неравенств -ОДЗ:
    корень из (х-5)(2х-3)=3
    х-5>0
    2х-3>0
    возводим в квадрат обе части уравнения: (х-5)(2х-3)=9
    2х²-3х-10х+15-9=0
    2х²-13х+6=0
    D=169-4*2*6=169-48=121
    первый ворень: х1=(13+11)/4=6 - удовлетворяет неравенствам ОДЗ, поэтому является корнем исходного уравнения
    второй корень: х2=(13-11)/4=1/2 - не принадлежит ОДЗ
    Ответ: 6

  • Решить неравенство \(\log_{x+1}(\frac{x}{3}-1)\cdot \log_{x+1}(x+2) < 0\)


    Решение: Давайте решим методом рационализации.
    log_h(f)×log_p(g) v 0 <=> (h-1)(f-1)(p-1)(g-1) v 0
    Очевидно, что по этой формуле наше неравенство равносильно следующему:
    х²(х/3 - 2)(х + 1) < 0
    Домножим на 3:
    х²(х - 6)(х + 1) < 0
    Корни каждой скобки: 0, 6 и -1 (0 - кратный корень)
    Отметим на числовой прямой и решим методом интервалов.
    - + -(-1)-(0)-(6)- + -> х
    Получили промежуток (-1; 0)∪(0; 6)
    Теперь учтем ОДЗ логарифмов.
    х + 1 > 0
    х + 1 ≠ 1
    х/3 - 1 > 0
    х + 2 > 0
    х > -1
    х ≠ 0
    х > 3
    х > -2
    В итоге: х ∈ (3; 6)
    Ответ: х ∈ (3; 6)

<< < 345 6 > >>