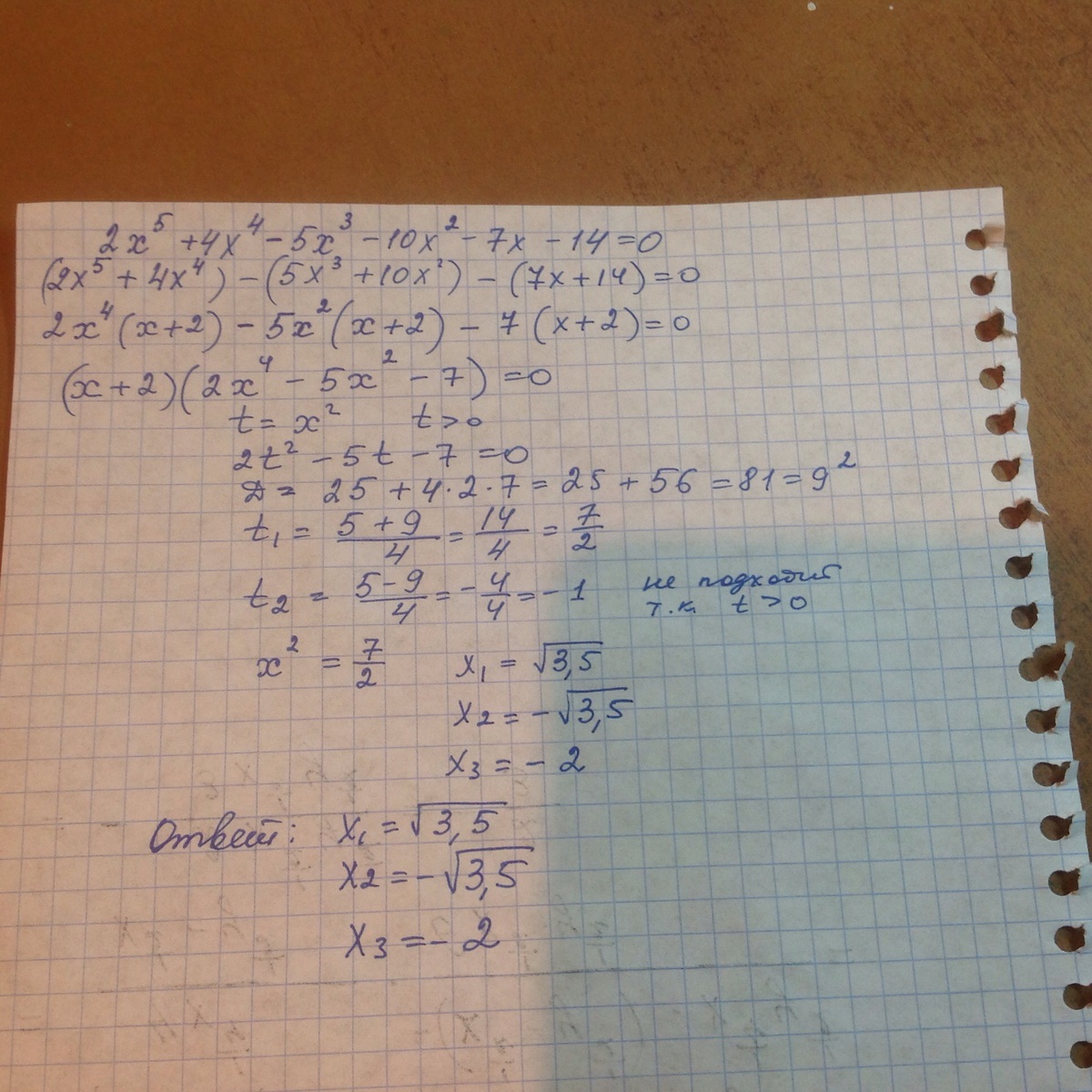решение уравнений »

найдите все корни уравнения - страница 2

  • График функции y=f(x) симметричен относительно прямой x=4 и уравнение f(x)=0 имеет 7 различных действительных корней. Найдите сумму этихкорней?


    Решение: Нули функции - это такое значение х, при котором функция y=f(x) равна нулю (то есть график функции пересекается с осью Х) .
    Для того, чтобы найти нули функции, надо функцию приравнять к нулю.
    Например, дана функция f(x) = х2 – 4 (икс в квадрате минус четыре)
    Приравниваем к нулю:
    х2 – 4 = 0
    А теперь решаем как квадратное уравнение, находим х (первое) = - 2, х (второе) = 2
    При этих значениях х функция y=f(x) = 0

    Этоможно сделать и графически. Просто построить функцию по точкам иначертить, точки пересечения графика с осью Х и будут нулями функции.

  • Найдите действительные корни уравнения: 2x^5+4x^4-5x^3-10x^2-7x-14=0 ; 4x^4-3x^3-8x^2+3x+4=0


    Решение: 1)2x^4(x+2)-5x²(x+2)-7(x+2)=0
    (x+2)(2x^4-5x²-7)=0
    x+2=0⇒x=-2
    2x^4-5x^2-7=0
    x²=a
    2a²-5a-7=0
    D=25+56=81
    a1=(5-9)/4=-1⇒x²=-1 нет решения
    a2=(5+9)/4=14/4⇒x²=7/2⇒x1=√14/2 U x=-√14/2
    x={-√14/2;√14/2}
    2)Разделим на х²
    4x²-3x-8+3/x+4/x²=0
    4(x²+1/x²)-3(x-1/x)-8
    4(x-1/x)²+8-3(x-1/x)-8=0
    x-1/x=a
    4a²-3a=0
    a(4a-3)=0
    a=0⇒x-1/x=0⇒(x²-1)/x=0⇒x²-1=0⇒x²=1⇒x=-1 U x=1
    4a-3=0⇒a=3/4⇒x-1/x=3/4⇒(4x²-3x-1)/4x=0
    4x²-3x-4=0
    D=9+64=73
    x1=(3-√73)/8
    x2=(3+√73)/8

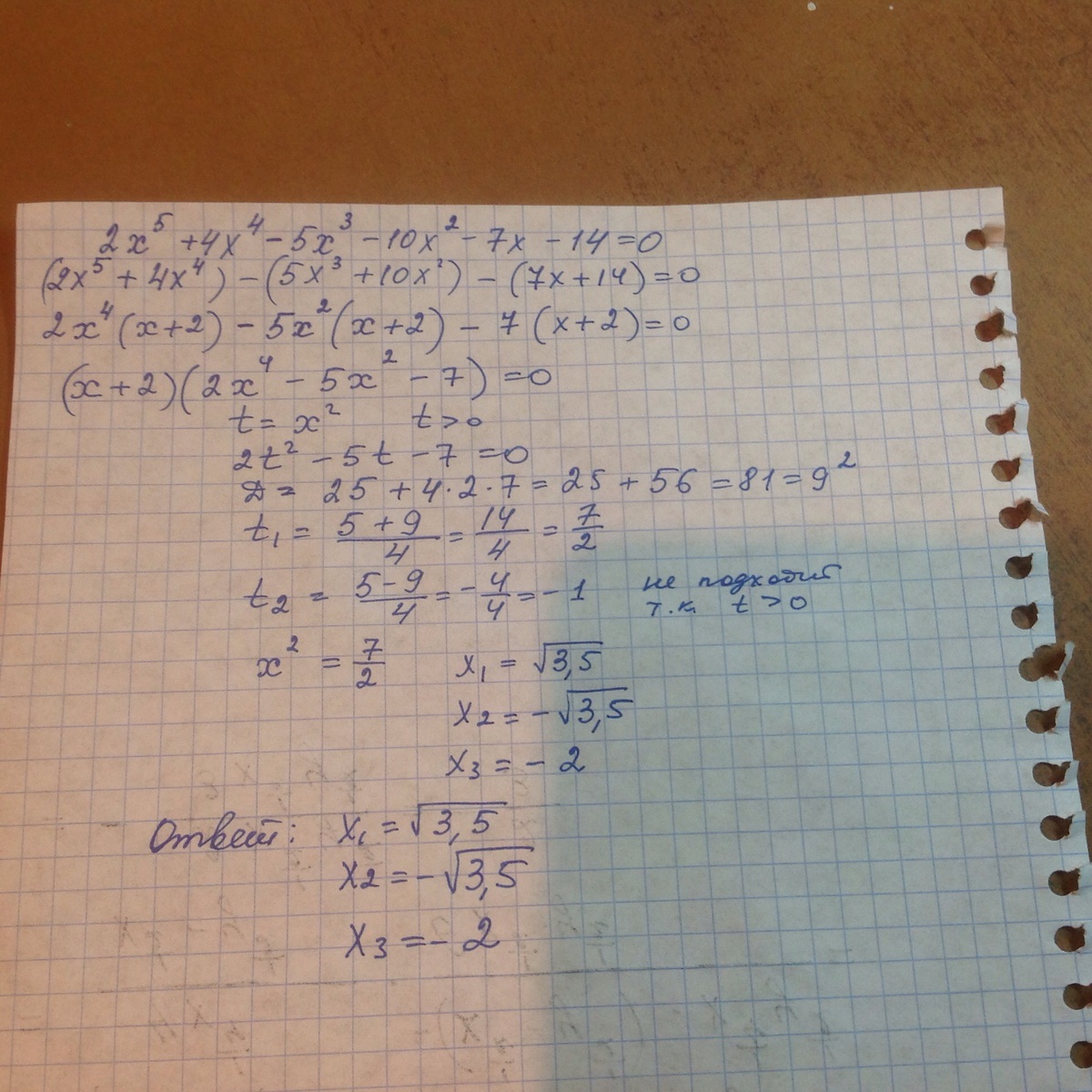
    x x - x x - x x x - x - x x - x - x - x a a - a- D a - - x - нет решенияa x x U x - x - Разделим на х x - x- x x x x - x- x - x- x - x- x - x- x a a - a a a- a x- x x - x x...

  • Найдите действительные корни уравнения 2х в кубе +7х в квадрате +4х + 3=0


    Решение: В уравнениях такого сорта корнями являются делители свободного члена. А это +-1 и +-3
    положительные числа не стоит проверять ( 0 не получится) .
    Будем проверять -1 и -3
    а) х = -1
    2·(-1)³ +7·(-1)² +4·(-1) +3 = 0(ложное равенство)
    б) х = -3
    2·(-3)³ + 7·(-3)² +4·(-3) +3=0 (истинное равенство)
    -54 +63 -12 +3
    Ответ: -3

  • Найдите действительные корни уравнения: |х²-х|=2


    Решение: $$ x^2-x=2 $$ или $$ x^2-x=-2 $$

    Первое уравнение:

    $$ x^2-x=2 $$
    $$ x^2-x-2=0 $$

    $$ \left \{ {{x_1+x_2=1} \atop {x_*x_2=-2}} \right. $$

    $$ \left \{ {{x_1=-1} \atop {x_2=2}} \right. $$

    Второе уравнение:

    $$ x^2-x=-2 $$
    $$ x^2-x+2=0 $$
    $$ D=1-4*2=1-8=-7 < 0 $$, значит, уравнение не имеет действительных корней.

    Ответ: $$ x_1=-1; x_2=2 $$

  • №1.Не решая квадратное уравнение х^2-204х+16=0, найдите значение выражения корень из х1, корень из х2, где х1-больший, а х2- меньший корень этого уравнения.
    №2. При каком значении параметра a уравнение 5(а+4)х^2-10х+а=0 имеет действительные корни одного знака.
    №3. Найдите все натуральные m, n, которые являются решениями уравнения 5^n-5^m=600.


    Решение: 1)
    Не решая квадратное уравнение х^2-204х+16=0 ???
    тогда по теореме Виета
    произведение корней уравнения равно 16
    произведение квадратных корней из корней уравнения равно 4 - это ответ
    2)
    №2. При каком значении параметра a уравнение 5(а+4)х^2-10х+а=0 имеет действительные корни одного знака.
    D=100-4*a*5(а+4)=100-20a^2-80a=-20*(a^2+4a-5)>0
    -5 < a < 4
    корни одного знака когда их произведение больше нуля
    воспользуемся теоремой Виета
    значит а/(а+4)>0 значит а>0 или а<-4

    ответ a є (-5;-4) U (0;4)
    3)
    5^n-5^m=600
    5^m*(5^(n-m)-1)=600=1*600=5*120=25*24
    a)
    5^m=1    ; m=0
    5^(n-m)-1    =600; - натуральных корней не имеет
    b)
    5^m=5    ; m=1
    5^(n-m)-1    =120; - натуральных корней не имеет
    c)
    5^m=25    ; m=2
    5^(n-m)-1    =24;
    n-m    =2
    n=4

    ответ n=4 m=2

<< < 12 3 4 > >>