решение уравнений »

найдите все корни уравнения - страница 4

  • Найдите корни уравнений, принадлежащие данному промежутку. cosφ=1, φ∈[-π;5π];


    Решение: Решение: φ=2πn, n∈Z   n=0,φ=2π*0=0   n=1,φ=2π   n=2,φ=2π*2=4π

  • Найдите корни уравнения, принадлежащие данному промежутку 2cos φ=√2, φ Є [-4π; 0]


    Решение: Cosφ = √2 / 2
    φ = ±arccos(√2 / 2)  + 2пk, kЄZ
    φ = ±п/4 + 2пk, kЄZ
    -4п<=φ<=0 (по условию)
    -4п<=п/4 + 2пk<=0 или -4п<=(-п/4) + 2пk<=0
    -9п/4<= 2пk<=-п/4 -7п/4<=2пk<=п/4
    -9/8<=k<=-1/8 -7/8<=k<=1/8
    k=1  k=0
    Подставляем значения k в наше значение угла, учитывая, что каждое относиться к этому выражению со своим знаком, 1-й k к выражению со знаком "+", 2-й со знаком "-" при п/4

    φ = п/4 + 2п*1, kЄZ φ = -п/4 + 2п*0, kЄZ
    φ = 9п/4, kЄZ φ = -п/4, kЄZ

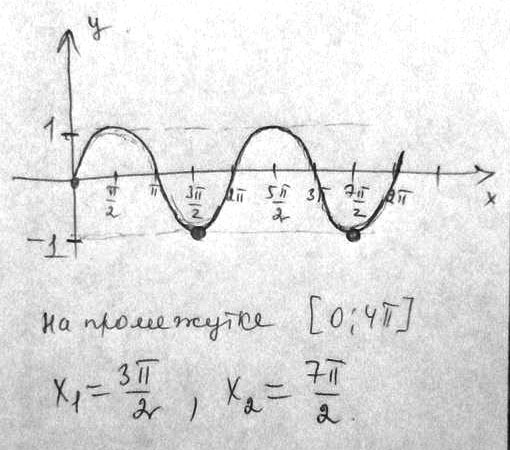
    Получили 2 значения угла с учетом промежутка, заданного условием.

  • Найдите корни уравнений, принадлежащие данному промежутку sinx=-1, x принадлежит [0; 4п]


    Решение: 3п/2 первый оборот. 7п/2- второй оборот

    Период функции равен 2п, поэтому здесь нужно найти корни двух одинаковых графиков у=sinx от о до 4п, на рисунке корни отмечены точкой

    п первый оборот. п - второй оборот Период функции равен п поэтому здесь нужно найти корни двух одинаковых графиков у sinx от о до п на рисунке корни отмечены точкой...

  • Найдите корни уравнений, принадлежащие данному промежутку: $$ 2sinx= \sqrt{3}, \\ x[-2 \pi;2 \pi ] $$
    У меня получились точки: \( \frac{ \pi }{3}; -\frac{5 \pi }{3} ; \frac{2 \pi }{3}; -\frac{4\pi}{3} \)
    В первых двух ответах использовал формулу \( arcsina+2 \pi n \)
    , во вторых двух - формулу \( \pi -arcsina+2 \pi n \)


    Решение: $$ 2\sin x= \sqrt{3} \\ \sin x= \frac{ \sqrt{3} }{2} \\ x=(-1)^k \arcsin\frac{ \sqrt{3} }{2} + \pi k, \\ k\in Z\\ x=(-1)^k \frac{ \pi }{3} + \pi k, \\ k\in Z $$
    Чтобы было удобнее решать неравенство распишем одну серию ответов через две:
    $$ \left[\begin{array}$ x=\arcsin\frac{ \sqrt{3} }{2}+2 \pi m, \\ m\in Z \\ x= \pi -\arcsin\frac{ \sqrt{3} }{2}+2 \pi n, \\ n\in Z \end{array}\right. \Rightarrow \left[\begin{array}$ x=\frac{ \pi }{3}+2 \pi m, \\ m\in Z \\ x=\frac{2 \pi }{3}+2 \pi n, \\ n\in Z \end{array}\right. $$
    Рассматриваем первую серию:
    $$ -2 \pi \leq \frac{ \pi }{3} +2 \pi m \leq 2 \pi \\ -2 \leq \frac{1 }{3} +2 m \leq 2 \\ -1 \leq \frac{1 }{6} + m \leq 1 \\ -1-\frac{1 }{6} \leq m \leq 1-\frac{1 }{6} \\ -\frac{7 }{6} \leq m \leq \frac{5 }{6} \\ m=-1: \\ x= \frac{ \pi }{3} -2 \pi = \frac{ \pi -6 \pi }{3} =- \frac{5 \pi }{3} \\ m=0: \\ x= \frac{ \pi }{3} +0= \frac{ \pi }{3} $$
    Вторая серия:
    $$ -2 \pi \leq \frac{2 \pi }{3} +2 \pi n \leq 2 \pi \\ -2 \leq \frac{2 }{3} +2 n \leq 2 \\ -1 \leq \frac{1 }{3} + n \leq 1 \\ -1-\frac{1 }{3} \leq n \leq 1-\frac{1 }{3} \\ -\frac{4 }{3} \leq n \leq \frac{2 }{3} \\ n=-1: \\ x= \frac{2 \pi }{3} -2 \pi = \frac{ 2\pi -6 \pi }{3} =- \frac{4 \pi }{3} \\ n=0: \\ x= \frac{ 2\pi }{3} +0= \frac{ 2\pi }{3} $$
    Ответ: -5π/3; -4π/3; π/3; 2π/3

  • Найдите корни уравнений, принадлежащие данному промежутку: $$ tgx=1, \\ x(\frac{\pi}{2} ; \frac{3\pi}{2} ) \\ \ cosx=- \frac{ \sqrt{3} }{2}, \\ x[- \pi ;\pi] $$
    Во втором уравнении по формуле косинуса плюс-минус arccosa + 2πn получаю 5π/6, что принадлежит отрезку по условию. Чтобы получить следующее решение надо же прибавить или отнять период косинуса, т.е. 2π?
    -5π/6 - если представить график функции, то он входит в отрезок [-π;π]. А как -5π/6 получить вычислением?


    Решение: $$ \mathrm{tg}x=1 \\ x= \frac{ \pi }{4} + \pi n, \\ n\in Z \\ \frac{ \pi }{2} < \frac{ \pi }{4} + \pi n < \frac{ 3\pi }{2} \\ \frac{ 1 }{2} < \frac{1 }{4} + n < \frac{ 3 }{2} \\ \frac{ 1 }{2}-\frac{1 }{4} < n < \frac{ 3 }{2}-\frac{1 }{4} \\ \frac{1 }{4} < n < \frac{ 5 }{4} \\ n=1: \\ x=\frac{ \pi }{4} + \pi =\frac{ 5\pi }{4} $$
    Ответ: 5π/4

    $$ \cos x=- \frac{\sqrt{3}}{2} \\ x=\pm \frac{5 \pi }{6}+2\pi n, \\ n \in Z \\ \left[\begin{array}$-\pi \leq \frac{5\pi}{6}+2\pi k\leq\pi \\ -\pi \leq-\frac{5\pi}{6}+2\pi m\leq\pi \end{array}\right. \\ \left[\begin{array}$-1\leq\frac{5}{6}+2k\leq1 \\ -1\leq-\frac{5}{6}+2m \leq1\end{array}\right. \\ \left[\begin{array}$-1-\frac{5 }{6}\leq2k\leq1-\frac{5}{6} \\ -1+\frac{5}{6}\leq2m\leq1+\frac{5}{6} \end{array}\right. $$
    $$ \left[\begin{array}$-\frac{11}{6}\leq2k\leq\frac{1}{6}\\ -\frac{1}{6}\leq2m\leq\frac{11}{6} \end{array}\right. \\ \left[\begin{array}$-\frac{11}{12}\leq k\leq\frac{1}{12}\\ -\frac{1}{12}\leq m\leq\frac{11}{12} \end{array}\right. \Rightarrow \left[\begin{array}$k=0: \\ x_1= \frac{5 \pi }{6}+0= \frac{5 \pi }{6} \\ m=0: \\ x_2= -\frac{5 \pi }{6}+0= -\frac{5 \pi }{6} \end{array}\right. $$
    Ответ: -5π/6; 5π/6

<< < 234 5 6 > >>