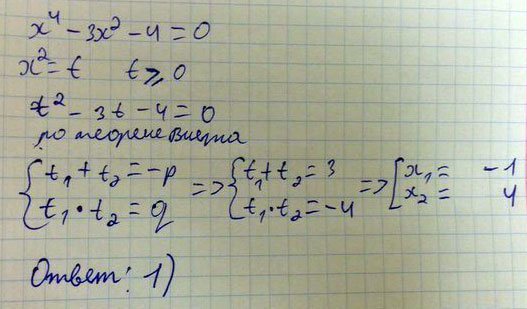решение уравнений »
решите уравнение - страница 3
Решите уравнение. 4sin(в 4 степени)2x+3cos4x-1=0
Решение: $$ 4\sin^4 2x + 3\cos 4x - 1 = 0\\ \left[ \cos 2x = \cos^2 x - \sin^2 x \right]\\ 4\sin^4 2x + 3(\cos^2 2x - \sin^2 2x) - 1 = 0\\ 4\sin^4 2x + 3\cos^2 2x - 4\sin^2 2x + \sin^2 2x - 1 = 0\\ \left[ \sin^2x - 1 = -\cos^2x \right]\\ 4\sin^2 2x(\sin^2 2x - 1) + 3\cos^2 2x - \cos^2 2x = 0\\ - 4\sin^2 2x \cos^2 2x + 2 \cos^2 2x = 0\\ 2\cos^2x (1 - 2\sin^2 2x) = 0 $$
$$ \left[ 1 - 2\sin^2 x = \cos 2x \right]\\ 2\cos^2 2x \cos 4x = 0\\ 1. \\ \cos 2x = 0\\ 2x = \pi n + \frac{\pi}{2}, \\ n \in \mathbb{Z}\\ \boxed{x = \frac{\pi}{2}n + \frac{\pi}{4}, \\ n \in \mathbb{Z}}\\ 2. \\ cos 4x = 0\\ \boxed{x = \frac{\pi}{4}n + \frac{\pi}{8}, \\ n \in \mathbb{Z}} $$
Решите уравнение (9х в 4 степени) в 5 степени * (3х) в 3 степени : (27х в 5 степени) в 4 степени = -192
Решение: Если раскрыть скобки получится 9 в 5ой х в 20ой * на 3 в 3ей х в 3ей : 27 в 4ой х в 20ой = -192 9-это 3 в квадрате ,а 27 - это 3 в кубе.(3 во 2ой) в 5ой х в 20ой * на 3 в 3ей х в 3ей : (3 в 3ей) в 4ой х в 20ой
получится - 3 в 13ой х в 23ей : на 3 в 12ой х в 20ой
равно= 3 в 1ой х в 3ей 3 в 1ой - это 3
3 х в 3ей = -192 -192 : 3 = -64
х в 3ей = -64
х=-4
Ответ:-4.
Решите уравнение х в 4 степени-3х в 3+4х в 2 -9х+3=0
Решение: x⁴-3x³+4x²-9x+3=0x⁴-3x³+x²+3x²-9x+3=0
x⁴+3x²-3x³-9x+x²+3=0
x²(x²+3)-3x(x²+3)+1(x²+3)=0
(x²-3x+1)(x²+3)=0
x²-3x+1=0
Δ=(-3)²-4*1*1
Δ=9-4
Δ=5
√Δ=√5
x₁=(-(-3)-√5)/(2*1)
x₁=(3-√5)/2x₂=(-(-3)+√5)/(2*1)
x₂=(3+√5)/2x²+3=0
x²=-3 ⇒ нет решения
Решите уравнение x ( в 4 степени) - 3 x (во 2 степени) - 4 = 0 1) -1; 4. 2) 1; 2. 3) -1; 1; -2; 2. 4) -2; 2
Решение: x^4 - 3x^2 - 4 = 0x^2 - 3x - 4 = 0
D= 9 - 4 * 1 * ( - 4)
D= 25
x1= 4
x2= -1
D -это дискриминант
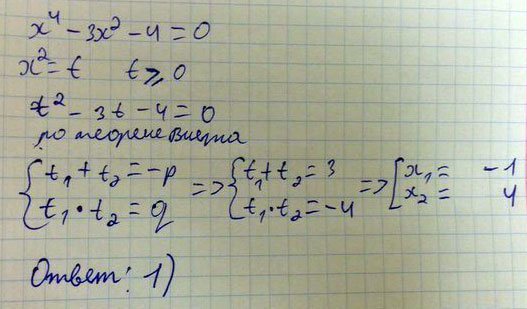
Решите уравнение: 1) х(в 4 степени) -22х(во 2 степени) - 75=0
2)х(в 4 степени) + 3х(во 2 степени)-28=0
Решение: Решение находится во вложении.