решите уравнение - страница 4
Решите уравнение: в)81х в 4 степени - 18х в кубе + х в квадрате = 0
г)27t в кубе + 36t в квадрате + 12t = 0
Решение: 1.$$ 81x^4-18x^3+x^2=0; $$
$$ 81x^2-18x+1=0;\\ D=0; \\ x_1=0;x_2= \frac{18+ \sqrt{0} }{162}; \\ x_2= \frac{1}{9} $$
2.$$ 27t^3+36t^2+12t=0; |:t \\ 26t^2+36t+12=0; \\ D=0; t_1= \frac{-12+ \sqrt{0} }{18} =- \frac{2}{3}; t_2=0 $$
81x^4 -18x³ +x² =0; ***(9x² -x)² =0****
x²((9x)² -2*(9x)*1 +1) =0;
x²(9x -1)² = 0 ;
[ x =0; 9x -1 =0. [ x=0; x=1/9.
ответ: 0 ; 1/9.
-------------------------
27t³ +36t² +12t =0 ;
3t(9t² +12t +4) =0;
3t(3t +2)² =0;
[ t =0; 3t +2 =0. [ t=0 ;t = - 2/3.
ответ: 0 ; - 2/3.
Решите графически уравнение -0.5x в 4 степени равно 4x
Решение: -0,5х^2-х+4=0 -график функции парабола (ветви направлены вниз).
найдём вершину параболы
х*=-в/2а
х*=1/-1
х*=-1
у (-1)*=4,5
так как график параболы симметричен, возьмём несколько значений х остальные точки построим симметрично.
х=0, значит у=4
х=1, значит у=2,5
х=2, значит у=0
по чертежу видно, что парабола пересекает ось ох в точках (2;0) и (-4;0)
ответ: (2;0) и (-4;0)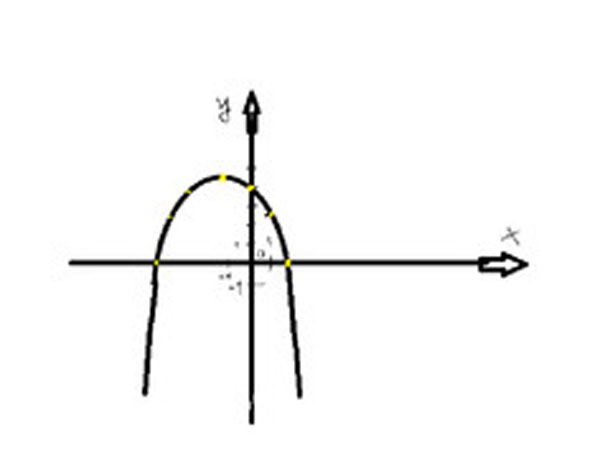
Решите уравнение : х(3-я степень)+3х(2-ая степень)-9х-27=0
Решение: Уравнение третьей степени решается способом группировки:х³+3х²-9х-27=0
(х³+3х²)-(9х+27)=0
х²(х+3)-9(х+3)=0
х²-9=0 х+3=0
х₁=3
х₂=-3
х₃=-3
Ответ: -3 ; 3.
Решить уравнения ^2-степень сравнения 1. у^2-4у=0
2.5у^2-2=0
3.10z^2+7z=0
4.x(3х-5)-4(3х-5)=0
5.2у(9у-6)+5(6-9у)=0
Решение:1. у^2-4у=0
у (у-4)=0
у=0 или у-4=0
у=4
2.5у^2-2=0
5у^2-2у=0
у(5у-2)=0
у=0 или 5у-2=0
3.10z^2+7z=0
z(10z+7)=0
z=0 или 10z+7=0
10z=-7
z=-0,7
4.x(3х-5)-4(3х-5)=0
3х²-5х-12х+20=0
3х²-17х+20=0
Д=289-4*3*20=289-240=49
д=7
х1=(17+7)/6=24/6=4 или х2= 17-7/6=10/6=1 ц 2/3
5.2у(9у-6)+5(6-9у)=0
18 у²-12у+30-45у=0
18 у² -57 у+30=0
Д= 3249-4*18*30=3249-2160=1089
д=33
х1=(57+33)/36=90/36=2,5
х2=(57-33)/36=24/36=2/3
последние да можно решить методом группировки слагаемых
Решить тригонометрическое уравнение: 3tg(2 степень)x+ctg(2 степень)x-4=0
Решение: Пусть tgx=t3t^2+1/t^2-4=0
(3t^4-4t^2+1)/t^2=0 t не равно нулю,т.е.tgx не равно нулю.x нe равно Пn n принадлежит Z
3t^4-3t^2-t^2+1=0
3t^2*(t^2-1)-(t^2-1)=0
(3t^2-1)*(t^2-1)=0
1.3t^2-1=0
t^2=1/3
1)t=(корень из 3)/3
tgx=(корень из 3)/3
x=П/6+Пk k принадлежит Z
2) t=-(корень из 3)/3
tgx=-(корень из 3)/3
x=-П/6+Пk k принадлежит Z
2. t^2-1=0
t^2=1
1)t=1
tgx=1
x=П/4+Пh h принадлежит Z
2)t=-1
tgx=-1
x= -П/4+Пh h принадлежит Z
Ответ: (+/-)П/6+Пk k принадлежит Z; (+/-)П/4+Пh h принадлежит Z

