решение уравнений »

дробное рациональное уравнение - страница 9

  • Дробно-рациональное уравнение \(\sqrt{3x-1}+\sqrt{x+3} = \sqrt{18-2x}\)


    Решение: ОДЗ
    3x+1≥0⇒x≥-1/3
    x+3≥0⇒x≥-3
    18-2x≥0⇒x≤9
    x∈[-1/3;9]
    Возведем в квадрат
    3x+1+2√(3x²+10x+3)+x+3=18-2x
    2√(3x²+10x+3)=18-2x-4x-4=14-6x
    √(3x²+10x+3)=7-3x
    Возведем в квадрат
    3x²+10x+3-49+42x-9x²=0
    6x²-52x+46=0
    3x²-26x+23=0
    D=676-276=400
    x1=(26-20)/6=1
    x2=(26+20)/6=23/3 =7 2/3

    1) ОДЗ:
    3x+1≥0⇒x≥-1/3
    x+3≥0⇒x≥-3
    18-2x≥0⇒x≤9
    x∈[-1/3;9]
    2) Возводим во вторую степень, т. е. в квадрат:
    3x+1+2√(3x²+10x+3)+x+3=18-2x
    2√(3x²+10x+3)=18-2x-4x-4=14-6x
    √(3x²+10x+3)=7-3x
    Возводим во вторую степень, т. е. в квадрат:
    3x²+10x+3-49+42x-9x²=0
    6x²-52x+46=0
    3x²-26x+23=0
    D=676-276=400
    x1=(26-20)/6=1 (подходит по ОДЗ)
    x2=(26+20)/6=23/3 =7 2/3 (подходит по ОДЗ)
    Ответ: 1; 7 2/3

  • Решите дробно-рациональное уравнение: \( \frac{x+3}{x-3}+ \frac{x-3}{x+3} = \frac{10}{3} \)


    Решение: $$ \frac{(x+3)^2+(x-3)^2}{(x+3)(x-3)} = \frac{10}{3} \\ \frac{ x^{2} +9+6x+ x^{2} +9-6x}{ (x-3)(x+3)}= \frac{10}{3} \\ \frac{2x^{2} +18}{ (x-3)(x+3)}= \frac{10}{3} \\ ({2x^{2} +18})*3={ (x-3)(x+3)}*10 \\ 6 x^{2} +54=10 x^{2} -90 \\ 4 x^{2} =144 \\ x^{2} =36 $$
    x=6 или x= - 6
    ОДЗ x-3$$ = $$0
    x+3$$ = $$0
    Ответ: 6; - 6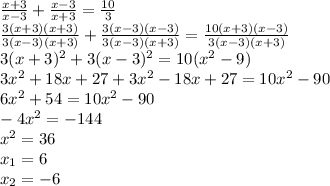

    frac x x- x x- frac frac x x x - x x- x frac frac x x- x frac x x- x x x - x x x или x - ОДЗ x- x Ответ -...

  • Решите дробное рациональное уравнение \(\frac{ x^{2} -6}{x-3} = \frac{ x}{x-3}\)


    Решение: $$ \frac{ x^{2} -6}{x-3} = \frac{ x}{x-3} \\ \frac{ x^{2} -6}{x-3} - \frac{ x}{x-3}=0 \\ \frac{ x^{2} -6-x}{x-3}=0 \\ \\ \left \{ {x^{2} -6-x=0}\atop {x -3 = 0} \right. \\ \left \{ {x^{2} -x-6=0}\atop {x = 3} \right. \\ \\ x^{2} -x-6=0 \\ D=(-1)^{2}-4*(-6)*1=1+24=25=5^{2} \\ x_{1}= \frac{-(-1)- \sqrt{25} }{2*1} = \frac{1-5}{2} = \frac{-4}{2} =-2 \\ x_{2}= \frac{-(-1)+ \sqrt{25} }{2*1} = \frac{1+5}{2} = \frac{6}{2} =3 \\ \left \{ {x=-2} \atop {x = 3} \right. $$
    Ответ: х= -2

  • Решите дробно-рациональное уравнение \( \frac{7x+2}{6x^2-5}+\frac{2x(3x+4)}{x+3}+\frac{17x+6}{2x(3x-2)} +\frac{6x^2+19}{1-x}=12\)


    Решение: Сумма 1-ой и 2-ой дроби после приведения к общему знаменателю равна $$ \frac{36x^4+48x^3-23x^2-17x+6}{(x+3)(6x^2-5)} $$.
    Сумма 3-ей и 4-ой минус 12 равна
    $$ \frac {36x^4+48x^3-23x^2-17x+6}{2x(3x-2)(1-x)} $$.
    Видим, что числители равны, т. е. надо решить уравнение
    $$ 36x^4+48x^3-23x^2-17x+6=0 $$.
    Младший коэффициент после деления на 36 равен 1/6, поэтому возникает подозрение, что корни 1/2 или 1/3. Действительно, оба подходят. Делением на 2х-1 и на 3х-1 находятся еще два корня -3/2 и -2/3.
    Теперь остается решить $$ \frac{1}{(x+3)(6x^2-5)}+\frac{1}{2x(3x-2)(1-x)}=0 $$. После приведения к общему знаменателю, числитель равен 28x²-9x-15, а его корни равны (9+√1761)/56 и (9-√1761)/56.

  • Решить через дробное рациональное уравнение. Из пункта А в пункт В велосипедист проехал по дороге длиной 48 км, обратно он возвращался по другой дороге, которая короче первой на 8 км. Увеличив на обратном пути скорость на 4 км/ч, велосипедист затратил на 1 ч меньше, чем на путь из А в В. С какой скоростью ехал велосипедист из пункта А в пункт В?


    Решение: Пусть х км/ч скорость из А в В, тогда скорость из В в А (х+4) км/ч. Время затраченное из А в В 48/х часов, а на обратный путь (48-8):(х+4). по условию задачи на обратный путь затрачено на 1 час меньше. Составляем уравнение.
    $$ \frac{48}{x} - \frac{40}{x+4} =1 $$
    общий знаменатель (х+4)*х
    48х+192-40х=х²+4х
    х²-4х-192=0
    D=16+4*192=784
    √D=√784=28
    x₁=(4+28):2=14
    x₂=(4-28):2=-12
    -12 не является решением к задаче
    14 км/ч скорость из А в В

<< < 789 10 11 > >>