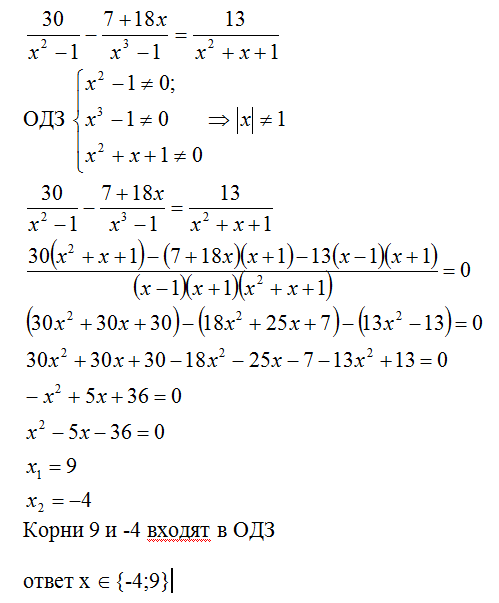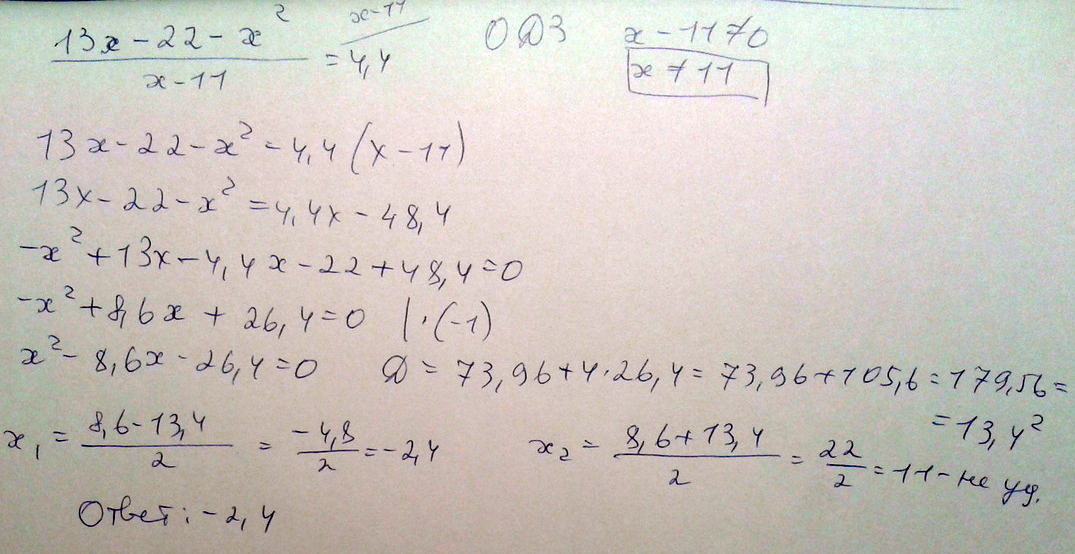решение уравнений »

дробное рациональное уравнение - страница 7

  • Решите дробно рациональное уравнение \(\frac{2x+1}{2x-1}+ \frac{8}{1-4x^2}= \frac{3(2x-1)}{7(2x+1)}\)


    Решение: $$ \frac{2x+1}{2x-1}+ \frac{8}{1-4x^2}= \frac{3(2x-1)}{7(2x+1)} \\\ x = \pm \frac{1}{2} \\\ 7(2x+1)^2-56=3(2x-1)^2 \\\ 28x^2+28x+7-56=12x^2-12x+3 \\\ 16x^2+40x-52=0 \\\ 4x^2+10x-13=0 \\\ D_1=25+52=77 \\\ x= \cfrac{-5\pm \sqrt{77} }{4} $$
    Ответ: $$ x= \cfrac{-5\pm \sqrt{77} }{4} $$

    (2x+1)/(2x-1) + 8/(1-4*x^2) = 3*(2x-1)/(7*(2x+1))
    ОДЗ х не равно 0,5 и не равно -0,5
    {7*(2x+1)^2 - 8*7 - 3*(2x-1)^2 } /(7*(4x^2-1)) = 0
    {7*(2x+1)^2 - 8*7 - 3*(2x-1)^2 } /(4x^2-1) = 0
    {7*(2x+1)^2 - 8*7 - 3*(2x-1)^2 } =0
    7*(4x^2+4x+1) - 56- 3*(4x^2-4x+1) =0
    16 x^2+40x-52=0
    4x^2+10x-13=0
    x1=(-5+корень(77))/4
    x2=(-5-корень(77))/4
    **********************

  • Решите дробно-рациональное уравнение Найдите корни уравнения 30/(x-1)(x+1) - 7/(x-1)(x^2+x+1) = 13/(x^2+x+1)


    Решение: 30/(x-1)(x+1) - 7/(x-1)(x^2+x+1) - 13/(x^2+x+1)=0
    (30(x^2+x+1)-(x+1)(7+18x)-13(x-1)(x+1))/(x-1)(x+1)(x^2+x+1)=0
    (30x^2+30x+30-7x-18x^2-7-18x-13x^2+13=0
    -x^2-5x-36=0 при (x+1)(x^3-1)≠0, т. е. x≠1 и x≠-1
    x^2-5x-36=0
    D=25+4*36=169
    x₁,₂=(5⁺₋√169)/2
    x₁=9
    x₂=-4

    Ваше решение
    ответ 9 и -4

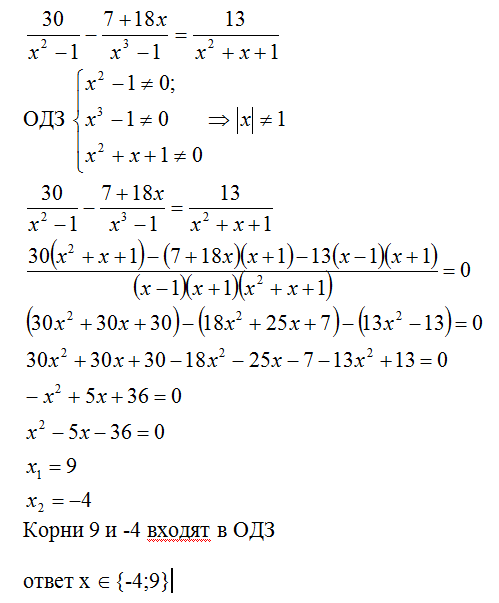
    x- x - x- x x - x x x x - x x - x- x x- x x x x x - x- x - - x- x -x - x- при x x - т. е. x и x - x - x- D x x x - Ваше решение ответ и -...

  • Решить дробно рациональное уравнение
    13x-22-x^2/x-11=4,4


    Решение:         Решение:
    13x-22-x^2=4,4x-11*4,4
    x^2-x(13-4,4)+22-11*4,4=0
    x^2-8,6x-26,4=0
    5x^2-43x-132=0
    x=(43+-67)/10
    x1=110/10=11
    x2=-2.4.

    Если есть неизвестное в знаменателе, обязательно надо делать ОДЗ.

            Решение x- -x x- x -x - - x - x- x - x- x - x x - . . Если есть неизвестное в знаменателе обязательно надо делать ОДЗ....

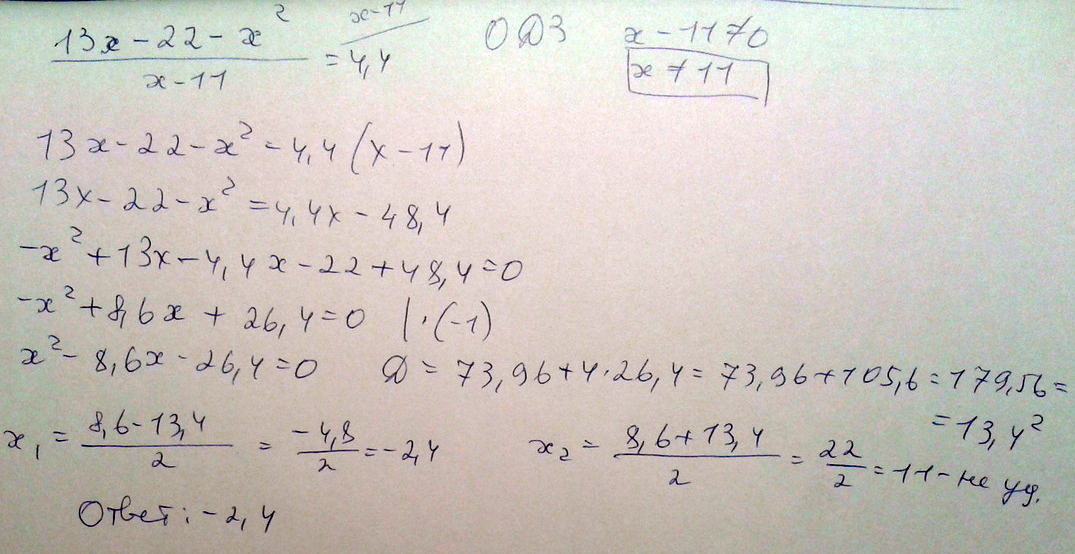
  • Решите дробно-рациональное уравнение \(\frac{5y^3-15y^2-2y+6}{y^2-9}=0\)
    \(\frac{3y^3-12y^2-y+4}{9y^4-1}=0\)


    Решение: 5у²(у-3)-2(у-3) (у-3)(5у²-2) 5у²-2
    = - = - = - ОДЗ х≠3 ; х≠-3
      (у+3)(у-3) (у+3)(у-3) у+3
    дробь равна 0 когда числитель рравен 0
    5у²-2=0
    5у²=2
    у²=2/5
    у=√2/5 и х=-√2/5
     
    (3у³-у)-(12у²-4) у(3у²-1)-4(3у²-1) (3у²-1)(у-4)
    = - = - = - =
      (3у²-1)(3у²+1) (3у²-1)(3у²+1) (3у²-1)(3у²+1)
      у-4
    = -=0 ⇒ у-4=0 у=4 ОДЗ 9у⁴-1≠0 сделаем замену у²=а
      2у²+1 9а²-1=0
      9а²=1
      а²=1/9
      а=1/3 и а=-1/3
      х₁=1/√3 решений ннет
      х₂=-1/√3

  • Решите дробно рациональных уравнение:
    2y-5 : y+5 = 3y+21 : 2y-1


    Решение: 2y - 5 : y + 5 = 3y + 21 : 2y - 1 ; ОДЗ : y не равен ( - 5 ) ; 0,5 ; (2y - 5 )( 2y - 1 ) = ( 3y + 21 )( y + 5 ) ; 4y^2 - 2y - 10y + 5 = 3y^2 + 15y + 21y + 105 ; 4y^2 - 3y^2 - 12y - 36y + 5 - 105 = 0 ; y^2 - 48y - 100 = 0 ; D = 2304 + 400 = 2704 ; корень квадратный 2704 = 52 ; y1 = ( 48 + 52 ) : 2 = 50 ( подходит ) y2 = ( 48 - 54 ) : 2 = - 3 ( подходит ) Ответ : 50 ; - 3

    $$ \frac{2y-5}{y+5} = \frac{3y+21}{2y-1} \\ \\ y+5 = 0 ; y = -5 \\ \\ 2y-1 = 0 ; y = \frac{1}{2} = 0.5 \\ \\ (2y-5)(2y-1) = (y+5)(3y+21) \\ \\ 4y^2-2y -10y +5 = 3y^2+21y + 15y+105 \\ \\ 4y^2-12y +5-3y^2 -36y-105 =0 \\ \\ y^2 -48y -100=0 \\ \\ D= (-48)^2 - 4*1*(-100) = 2304+400= 2704 = 52^2 \\ \\ y1= \frac{48-52}{2} = \frac{-4}{2} = -2 \\ \\ y2= \frac{48+52}{2} = \frac{100}{2} = 50 $$
    Ответ: y₁=-2 ; y₂=50

<< < 567 8 9 > >>