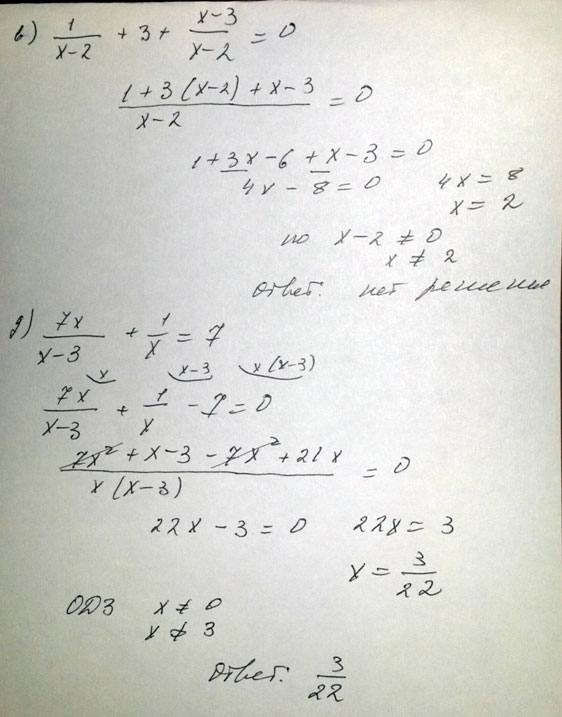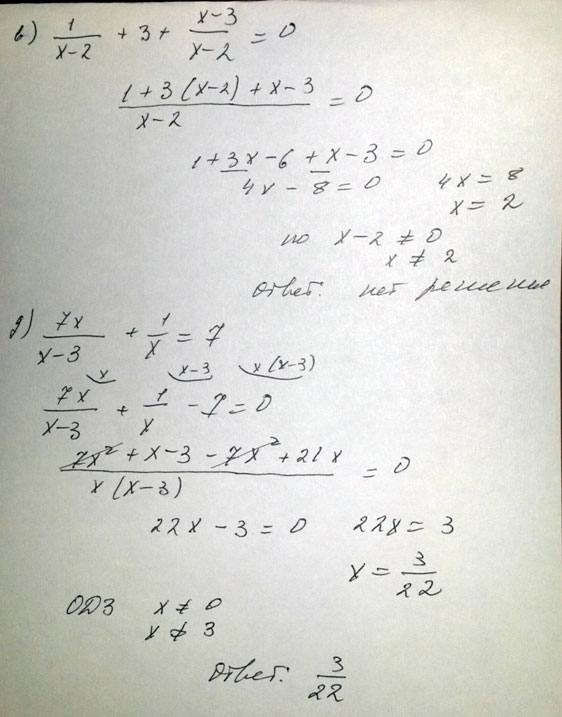дробное рациональное уравнение - страница 8
Решите дробно рациональных уравнение:
5x-2 : x+2 = 6x-21 : x-3
Решение: ( 5х - 2 ) : ( Х + 2 ) = ( 6х - 21 ) : ( Х - 3 )
( Х - 3 )( 5х - 2 ) = ( Х + 2 )( 6х - 21 )
5х^2 - 2х - 15х + 6 = 6х^2 - 21х + 12х - 42
5х^2 - 17х + 6 = 6х^2 - 9х - 42
6х^2 - 5х^2 - 9х + 17х - 42 - 6 = 0
Х^2 + 8х - 48 = 0
D = 64 + 192 = 256 ; V256 = 16
X1 = ( - 8 + 16 ) : 2 = 4
X2 = ( - 8 - 16 ) : 2 = - 12
ОДЗ : Х не равен ( - 2 ) ; 3 ; Ответ : 4 ; - 12при условии, что х не равен -2 и 3, получаем:
(5х-2)(х-3) = (6х-21)(х+2)
5х²-15х-2х+6=6х²+12х-21х-42
5х²-17х+6=6х²-9х-42
5х²-17х+6-6х²+9х+42=0
-х²-8х+48=0
D=256
x=12 корень уравнения
x= - 4 корень уравнения
Решите дробно рациональное уравнение 60/х=23-х
Решение: 1) Так как в уравнении имеется дробь, то необходим общий знаменатель. Здесь общий знаменатель Х:
$$ \frac{60}{x} - \frac{(23-x)x}{x} =0 \\ \frac{60-23x+x^{2} }{x} =0 $$
ОДЗ (область допустимых значений): $$ x = 0 $$
2) Опуская знаменатель дроби, решим числитель:
$$ x^{2} $$-23x+60=0
D=$$ 23^{2} - 4*60= 17^{2} $$
x1=20
x2=3
Ответ: 3; 20Вот, квадратное уравнение, на фото решение
Решите путем дробных рациональных уравнений. Катер прошел 15 км против течения и 6 км по течению, затратив на весь путь столько же времени, сколько ему потребовалось бы, если бы он шел 22 км по озеру. Какова собственная скорость катера, если известно, что скорость течения реки равна 2 км/ч?
Решение: Х км/час -скорость катера в стоячей воде (в том числе и на озере)
х+2 км/час - скорость по течению,
х-2 км/час - скорость против течения
$$ \frac{15}{x-2}+\frac{6}{x+2}=\frac{22}{x},\; \; \; xe \pm 2\\\\15x(x+2)+6x(x-2)=22(x^2-4)\\\\x^2-18x-88=0\\\\x_1=-4,\; ne\; \; podxodit(-4<0)\\\\x_2=22 $$Решение:
Пусть х - собственная скорость катера. Тогда (x+2) - скорость и течения, и катера; (x-2) - скорость катера против течения. Известно, что второй пусть он прошел 15 км, а второй - 6 км. Его все время пути можно записать в выражении:
$$ \frac{15}{x-2}+\frac{6}{x+2} $$
Однако нам дано еще, что в озере при прохождении пути в 22 км он бы за столько же времени. По смыслу задачи в озере течения нет, поэтому скоростью течения можно пренебречь. Его время пути можно записать в следующем выражении:
$$ \frac{22}{x} $$
Отсюда мы получаем уравнение относительно времени:
$$ \frac{15}{x-2}+\frac{6}{x+2}=\frac{22}{x} $$
Преобразовывая уравнение, в заключение мы получим квадратное уравнение:
$$ x^2-18x-88=0 \\ D=324+354=26^2 \\ x_1=\frac{18+26}{2}=22 \\ x_2=\frac{18-26}{2}=-4 $$
Второй корень нам не подходит по смыслу задачи по одной простой причине, что он отрицателен. Поэтому скорость катера была равна 22 км/ч
Ответ: 22 км/ч
Нужно составить дробно-рациональное уравнение. С одной переменной.
Мастер и ученик работая совместно могут выполнить задание за 6 ч 40мин. если сначала будет работать только мастер и выполнит половину задания, а
затем его сменит ученик и выполнит оставшуюся часть задания, то всего на выполнение задания будет израсходовано 15 часов. За сколько часов может выполнить задание мастер и за сколько ученик, работая в отдельности?
Решение: Пусть половину задания мастер выполнит за х ч,
а ученик - за 15-х часов. Соответственно целое задание мастер выполнит за 2х часов, а ученик - за 2(15-х) часов.
Вместе они работали 6 2/3 ч и выполнили одно (целое) задание.
Тогда, по условию задачи можно составить уравнение:
$$ \frac{ \frac{20}{3} }{2x}+ \frac{ \frac{20}{3} }{2(15-x)}=1\\\\ \frac{20}{3}(15-x)+ \frac{20}{3}x=2x(15-x)\\\\100- \frac{20}{3}x+ \frac{20}{3}x=30x-2x^2\\\\2x^2-30x+100=0\\\\x^2-15x+50=0\\\\D=(-15)^2-4*1*50=225-200=25=5^2\\x_1=5\\x_2=10 $$
Итак, мы нашли время, за которое мастер и ученик, соответственно выполнят каждый половину задания. Значит, увеличив результаты в 2 раза, получим время на выполнение всего задания.
5*2=10 (ч)- время мастера
10*2=20(ч) - время ученикаРешить дробно рациональное уравнение а) \(\frac{2}{x-2} = \frac{5}{x+4}\)
в) \(\frac{1}{x-2} +3+ \frac{x-3}{x-2}\)
д) \(\frac{7x}{x-3}+\frac{1}{x}=7\)
Решение: В первом уравнении нет корней, второе имеет корень х=3/22$$ a) \frac{2}{x-2} = \frac{5}{x+4} \\ 2x+8=5x-15 \\ -3x=-23 \\ x= \frac{23}{3}. \\ b) \frac{1}{x-2} +3+ \frac{x-3}{x-2} $$
Приводим к общему знаменателю:
$$ \frac{1+3x-6+x-3}{x-2} =0 $$
Знаменатель дроби не может быть равен 0, поэтому:
х - 2 ≠ 0
х ≠ 2
Дробь равна 0, когда её числитель равен 0:
4х - 8 = 0
х = 8/4 = 2.
Но х не может быть равен 2, поэтому задача не имеет решения.
д) Приводим к общему знаменателю и приравниваем числители полученных дробей:
$$ 7x^2+x-3=7x^2-21x $$
22x = 3
x = 3/22.