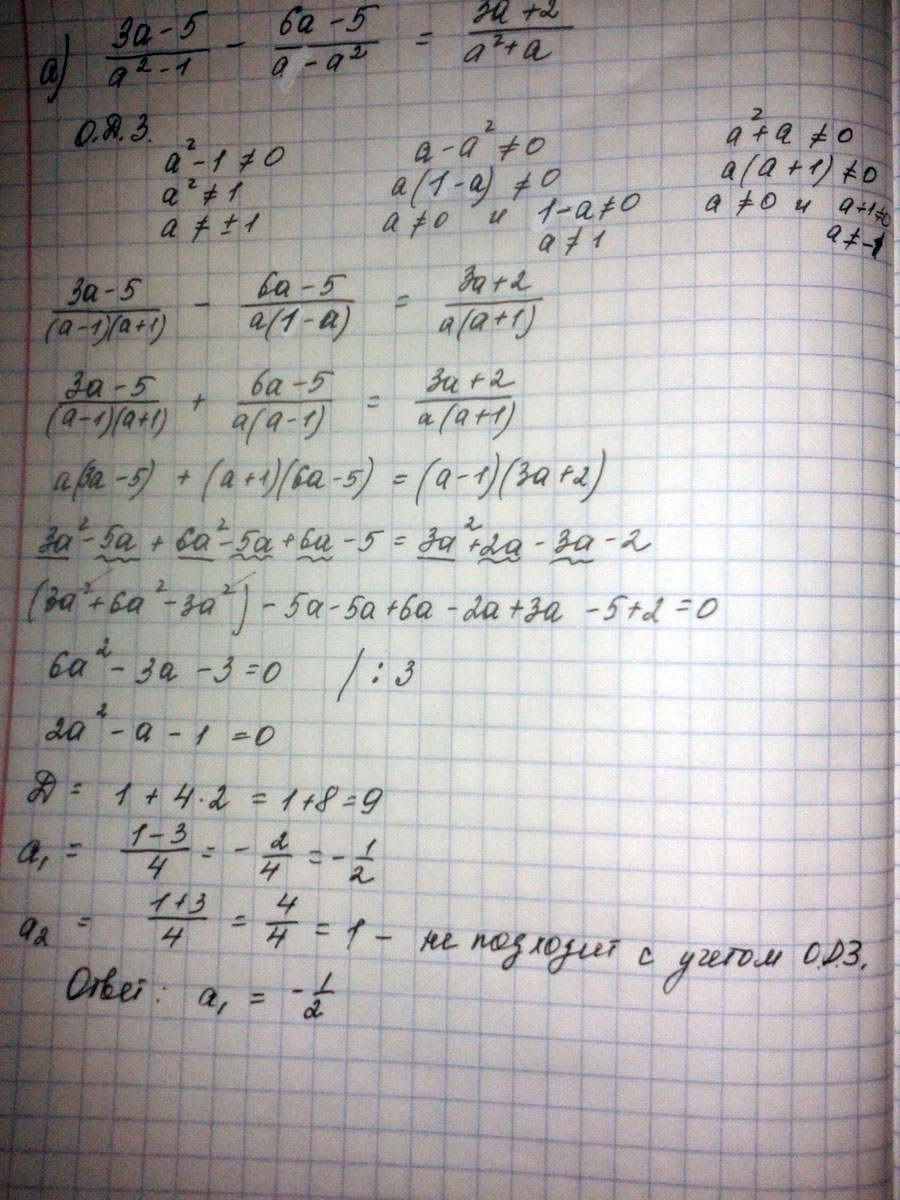решение уравнений »

дробное рациональное уравнение - страница 5

  • Дробные рациональные уравнения \(\frac{3a-5}{a^2-1}-\frac{6a-5}{a-a^2}=\frac{3a+2}{a^2+a}\)


    Решение: (3a-5)/(a-1)(a+1) +(6a-5)/a(a-1)=(3a+2)/a(a+1)
    ОЗ а(а-1)(а+1)≠0⇒а≠0 и а≠1 и а≠-1
    (3a-5)*a+(6a-5)*(a+1)=(3a+2)*(a-1)
    3a²-5a+6a²+6a-5a-5-3a²+3a-2a+2=0
    6a²-3a-3=0
    D=9+72=81
    a1=(3-9)/12=-1/2
    a2=(3+9)/12=1 не удов усл
    Ответ а=-1/2

    Решение смотри :

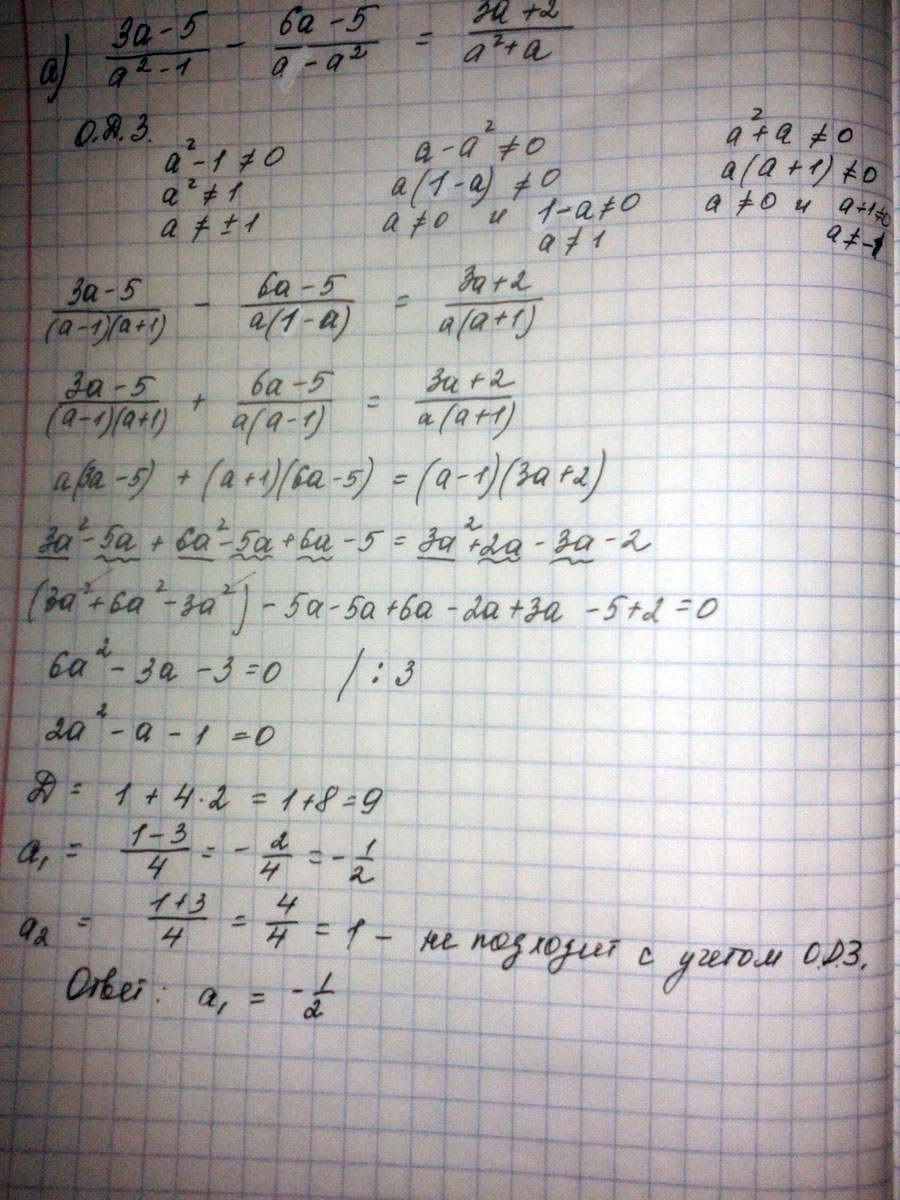
    a- a- a a- a a- a a a ОЗ а а- а а и а и а - a- a a- a a a- a - a a a- a- - a a- a a - a- D a - - a не удов услОтвет а - Решение смотри...

  • Обьясните, как решать дробно-рациональные уравнения напримере этого:
    х²+3/х²+1=2


    Решение: Числитель и знаменатель нужно писать в скобках, чтобы не было ошибочного понимания уравнения.(х²+3) / (х²+1) =2.
    Переносим 2 в левую часть и приводим к общему знаменателю.
    (х²+3) / (х²+1) - 2 =0, к 2 дополнительный множитель х²+1
    (х²+3 -2х²-2) / (х²+1) =0. Теперь числитель равен 0, а знаменатель не равен.
    -х²+1 = 0 и х²+1 ≠0
    В первом уравнении х² = 1 
    х=1 илих=-1. Оба корня удовлетворяют условию не равно 2≠0.
     Ответ 1; -1.

  • Нужно решить рациональные уравнения, знак "/" - дробь.
    1) 2/x + 1/x-2 = 2
    2) 5/x+1 + 4/x-2 = 3/x-3


    Решение: 1) 2/x + 1/x -2 =2

    приведем в общему знаменателю.

    2x-4+x/ x(x-2)=2x^2-4x; знаменатель можно убрать, т. к это уравнение.

    3x-4-2x^2+4x=0; умножим на (-1);

    2x^2+ 7x +4=0;

    D= sqrt(16)=4^2

    x1= -7+4/4=-(3/4);

    x2=-7-4/4=-(11/4);

    Ответ: -(3/4); -(11/4);

    2) аналогично: 5(x-2)(x-3)+4(x+1)(x-3)=3(x+1)(x-2); переумножаем и правую часть переносил влево.

    5x^2-25+30+4x^2-8x-12-3x^2+3x+6=0

    отсюда будет x^2+5x+4=0;

    D= sqrt(16)=4^2

    x1=-5+4/2=-1/2;

    x2=-9/2=-6,5

    Ответ: -1/2; -6.5;

    sqrt-корень

  • Тема: рациональные уравнения.
    Пример: х + 1 / х + 4 = 2 / х + 4
    ОДЗ х + - (плюс минус) 4 ≠ 0; х ≠ - 4
    х + 1 = 2
    х = 2 - 1
    х = 1
    Ответ: 1
    А теперь то, что нужно решить:
    1) 2у / у - 5 = 5 / у - 5
    2) 16 / x^2 + 1 = х^2 + 1
    3) 4у + 3 / у - 7 = у^2 / 7 - у
    4) 1 / 3х - 1 = х / 27 - х


    Решение: 1.2y/y-5 =5/y-5 2.16/x^2+1=x^2+1
    ОДЗ: y не равен 5 x^4+2x^2-15=0
    2y=5 x^4+5x^2-3x^2-15=0
    y=2.5 (x^2+5)(x^2-3)=0
    Ответ: 2.5 x^2=-5 x не существует
    x^2=3 x=+-корень из 3
    Ответ:+-корень из 3
    3.4y+3/y-7=y^2/7-y 4.1/3x-1=x/27-x
    ОДЗ:y не равен 7 1/3x-1 -x/27-x=0
    4y+3=-y^2 (27-x-3x^2+x)/(3x-1)(27-x)=0
    y^2+4y+3=0 3(3-x)(3+x)=0
    y^2+3y+y+3=0 x=+-3
    y=-1 Ответ:+-3
    y=-3
    Ответ: -3;-1

  • Числитель обыкновенной дробина 2 меньше знаменателя. Если числитель увеличить на 1, а знаменатель увеличить на 3, то получится дробь, равная данной. Найдите данную дробь


    Решение:    x/(x+2)=(x+1)/(x+2+3)                

            x/(x+2)=(x+1)/(x+5)                   x≠-2, x≠-5

            x(x+5)=(x+2)(x+1)

            x²+5x=x²+3x+2

            2x=2

            x=1

            Ответ: дробь равна 1/3

<< < 345 6 7 > >>