корни »

найдите корни уравнения, принадлежащие отрезку - страница 2

  • Решите уравнение 2cos^2x-9sinx-6=0 и найдите корни принадлежащие отрезку [п/2;3п/2]


    Решение: $$ 2cos^2x-9sinx-6=0 $$
    $$ 2(1-sin^2x)-9sinx-6=0 $$
    $$ 2sin^2x+9sinx+4=0 $$
    sinx=t
    $$ 2 t^{2} +9t+4=0 $$
    $$ t_{1,2}=-4;- \frac{1}{2} $$
    $$ sinx=- \frac{1}{2} $$
    $$ x=(-1)^n (-\frac{ \pi }{6})+ \pi n $$, n∈Z
    $$ x=(-1)^{n+1} \frac{ \pi }{6}+ \pi n $$, n∈Z
    при n=1 $$ \pi + \frac{ \pi }{6} = \frac{7 \pi }{6} $$ ∈ \( [ \frac{ \pi }{2}; \frac{3 \pi }{2} ] \)

  • а) Решить уравнение cos(2x) + 3sin^2(x) = 1,25
    б) найдите корни, принадлежащие отрезку [π 5π/2]


    Решение:

    Используя формулу косинуса двойного угла, сведем данное уравнение к квадратному относительно переменной синус х (так как фигурирует в уравнении квадрат синуса)

    $$ cos(2x)+3sin^2 x=1.25;\\1-2sin^2 x+3sin^2 x=1.25;\\sin^2 x=0.25 $$

    отсюда либо $$ sin x=0.5; x=(-1)^k*\frac{\pi}{6}+\pi*k $$ k є Z

    либо $$ sin x=-0.5;x=(-1)^{n+1}*\frac{\pi}{6}+\pi*n $$ n є Z

    обьединяя $$ x=^+_-\frac{\pi}{6}+\pi*k $$k є Z

    обозначив на кругу, и учититывая нужный указанный промежуток находим корни

    $$ \frac{7*\pi}{6};\frac{11*\pi}{6};\frac{13*\pi}{6} $$

  • Решите уравнение 6sin^2 x - 5sin x -4 =0 и найдите корни,принадлежащие отрезку [-7pi/2 ;-3pi/2]


    Решение: D = sqrt(25 + 4 * 4 * 6) = 11

    sin x1 = (5 + 11)/12 > 1 - не имеет решения

    sin x2 = (5 - 11)/12 = -1/2

    $$ x_2 = 2\pi k + \frac{3\pi}{2} \pm \frac{\pi}{3} $$

    Из области определения подходят корни

    $$ x = -\frac{5\pi}{2} \pm \frac{\pi}{3} $$

    Часит а)

    Для начала синус надо заменит с каким либо буквой, я его заменю на t ОДЗ -1<=t<=1

     6t^2-5t-4=0

    D=25+96=121=11^2

    t1=16/12 не подлежить ОДЗ

    t2=-6/12=-1/2

    общий ответ (-1)в степени n arcsin(-1/2)+Pi n, где n принадлежить целому числу.

  • Найдите корни уравнения, принадлежащие отрезку [0:2пи] (sin x- 1/2)*(sinx+ 1)=0


    Решение: (sin x - 1/2)*(sinx + 1) = 0

    совокупность 2-х решений
    sinx = 1/2 ==> x = pi/6 + 2pik, x = 5pi/6 + 2pik,k     ∈ Z
    sinx = - 1 ==> x = - pi/2 + 2pik. k     ∈ Z

    + отбор корней внутри фото  sin x - sinx      совокупность -х решенийsinx x pi pik x pi pik k  Zsinx - x - pi pik. k  Z отбор корней внутри фото ...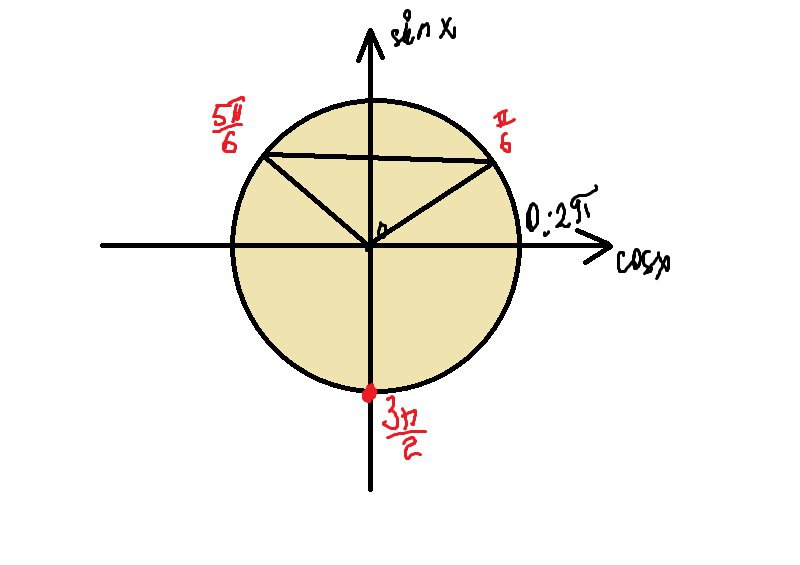

  • Решите уравнение 2sin^4x + 3cos2x + 1 = 0. Найдите все корни, принадлежащие отрезку [пи;3пи].


    Решение: 2*(1-cos2x)²/4+3cos2x+1=0
    (1-cos2x)²+6cos2x+2=0
    1-2cos2x+cos²2x+6cos2x+2=0
    cos²2x+4cos2x+3=0
    a=cosx
    a²+4a+3=0,a1+a2=-4 U a1*a2=3
    a1=-1,cosx=-1⇒x=π+2πn
    a2=-3,cosx=-3∉[-1;1]
    x=π;3π

    2 sin⁴x +3cos2x +1=0
    2 sin⁴x+3(cos²x-sin²x)+1=0
    2 sin⁴x+3(1-sin²x-sin²x)+1=0
    2sin⁴x+3(1-2sin²x)+1=0
    2sin⁴x+3-6sin²x+1=0
    2sin⁴x-6sin²x+4=0
    sin⁴x-3sin²x+2=0

    Пусть у=sin²x
    y²-3y+2=0
    D=9-8=1
    y₁=3-1=1
      2
    y₂=3+1=2
      2

    При у=1
    sin²x=1
    sin²x-1=0
    (sinx-1)(sinx+1)=0
    sinx-1=0 sinx+1=0
    sinx=1 sinx=-1
    x=π + 2πn x=-π + 2πn
      2 2

    При у=2
    sin²x=2
    sin²x-2=0
    (sinx-√2)(sinx+√2)=0
    sinx-√2=0 sinx+√2=0
    sinx=√2 sinx=-√2
    √2∉[-1; 1] -√2∉[-1; 1]
    нет решений нет решений

    x∈[π; 3π]
    х=π + 2πn
      2
    π≤ π+2πn ≤3π
      2
    π- π ≤ 2πn ≤ 3π - π 
      2 2
    π ≤ 2πn ≤ 5π 
    2 2
    π : 2π ≤ n ≤ 5π : 2π
    2 2
    π *  1 ≤ n ≤ 5π * 1
    2 2π 2 2π
    1/4 ≤ n ≤ 5/4
    0.25 ≤ n ≤ 1.25
    n=1
    x=π + 2π*1 = 5π 
      2 2

    x=-π +2πn
      2
    π ≤ -π + 2πn ≤ 3π
      2
    π + π ≤ 2πn ≤ 3π  + π 
      2 2
    3π ≤ 2πn ≤ 7π
     2 2
    3π * 1 ≤ n ≤ 7π *  1
     2 2π 2 2π
    3/4 ≤ n ≤ 7/4
    0.75 ≤ n ≤ 1.75
    n=1
    x= -π + 2π *1 = 3π
      2 2

    Ответ: 3π ; 5π
      2 2

<< < 12 3 4 > >>