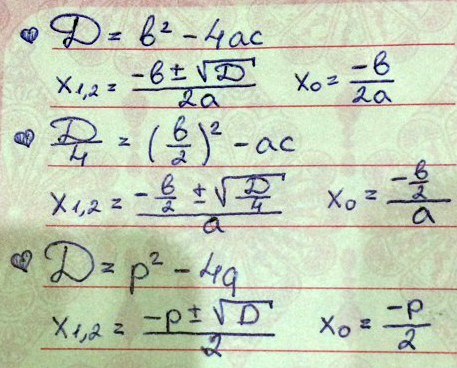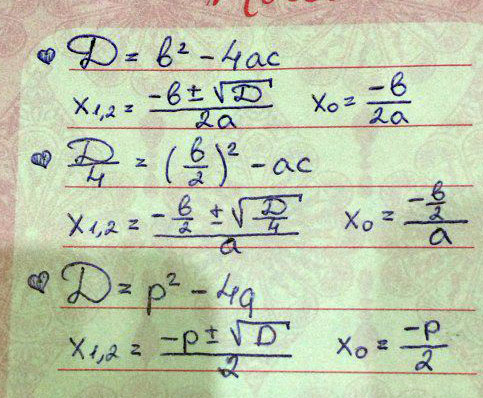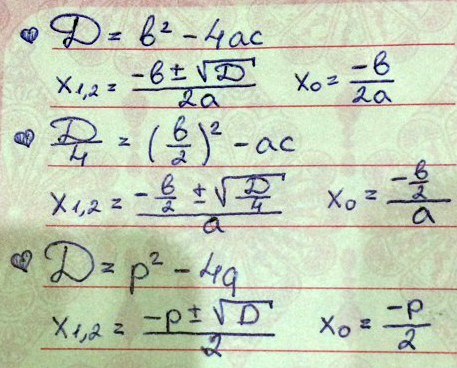преобразуйте выражения, используя формулы сокращенного умножения - страница 2

представьте второе слагаемое трёхчлена в виде алгебраической суммы подобных слагаемых и разложите трёхчлен на множители применив способ группировки:

х в 2 степени - 6х +8= разложите многочлен на множители используя приём выделения квадрата двучлена: х в 2 степени -2х-24= разложите многочлен на множители используя соответствующую формулу сокращённого умножения: у в 6 степени/125(дробь)+0,064= разложите многочлен на множители: 5а+аb в 2 степени - a в 2 степени b - 5b=

1) x^2 - (4x+2x)+8= x^2 - 4x - 2x+8=(x^2 - 4x) - (2x - 8)=x(x - 4) -2()x - 4)=(x - 4)(x - 2)

2) x^2 - 2x - (16+8)= (x^2 - 16) - (2x - 8)= (x - 4)(x+4) - 2(x - 4)=(x - 4)(x+4 -2)=(x - 4)(x+2)

3) y^6  +0,4^3=( (0,2y)^2+0,4)( (0,2y)^4 - 0,016y^2 + 0,16) =

  5^6

4) 5а+аb^2 - a^2b - 5b=(5а- 5b)+(аb^2 - a^2b)=5(а- b)- ab(a - b)=(5 - ab)(a - b)

Составьте многочлен p (x)=2p1(x)+p2(x)-p3(x) и запишите его в стандартном виде,если: 1. p1(x)=-3x(-3x во 2-ой степени) p2(x)=1-x

p3(x)=x^2(во 2-ой степени)-4x
2. a)(2m+1)(4-m) б)25m^2-30mn^2):(-5mn)
3. Упростите используя формулы сокращённого умножения: (3x+4)(4-3x)-(2x+1)^2
4. Докажите что выражения не зависит от переменной: 3*(1-2y)(1+2y+4y^2)+4*(6y^3-1)

1. p1(x)=-3x²

p2(x)=1-x

p3(x)=x²-4x

p (x)=2*(-3x²)+1-x-(x²-4x)=-6x²+1-x-x²+4x=-7x²+3x+1

2. a)(2m+1)(4-m)=8m-2m²+4-m=-2m²+7m+4

б)25m^2-30mn^2):(-5mn)=25m²:(-5mn)-30mn²:(-5mn)=-5m/n+6n

3. упростите используя формулы окращённого умножения:

(3x+4)(4-3x)-(2x+1)²=16-9x²-(4x²+4x+1)=16-9x²-4x²-4x-1=-13x²-4x+15

4. докажите что выражения не зависит от переменной:

3*(1-2y)(1+2y+4y²)+4*(6y³-1)=3*(1-8y³)+24y³-4=3-24y³+24y³-4=-1 значит не зависит от переменной

Упростите выражение а) 2√3 - √27 + 2√48
б) √8 + 2√18 - √72
в) 2√20 - √35 - 2√12
г) 2√28 - 0,5√24 + 2√7

Преобразуйте выражение, используя формулы сокращенного умножения
а) (2 + √3)(2 - √3)
б) (√6 - 1)(√6 + 1)
в) (√7 - √5)(√7 + 5)
г) (1-√5)^2
д) (√3 - √5)^2
е) (5 - √5)^2 + 5√5

а) 2√3 - √27 + 2√48
$$ 2 \sqrt{3}- \sqrt{27}+2 \sqrt{48}= 2\sqrt{3}- \sqrt{3^23}+2 \sqrt{4^23}= \sqrt{3}(2-3+8)= 7 \sqrt{3} $$
б) 
√8 + 2√18 - √72
$$ \sqrt{2^22}+2 \sqrt{3^22} - \sqrt{6^22}= \sqrt{2} (2+6-6)=2 \sqrt{2} $$
в) 2√20 - √35 -  2√12
$$ 2 \sqrt{2^25}- \sqrt{5*7}-2 \sqrt{2^23}=4 \sqrt{5}- \sqrt{5*7}-4 \sqrt{3} $$
г) 2√28 - 0,5√24 + 2√7
$$ 2 \sqrt{2^2*7}-0.5 \sqrt{2^2*6}+2 \sqrt{7} =6 \sqrt{7}- \sqrt{6} $$

Преобразуйте выражение, используя формулы сокращенного умножения 
а) (2 + √3)(2 - √3)=4-3=1
б) (√6 - 1)(√6 + 1)=6-1=5
в) (√7 - √5)(√7 + 5)=7-5=2
г) $$ (1 - √5)^2= 1-2 \sqrt{5}+5=6-2 \sqrt{5} $$
д) (√3 - √5)^2=$$ 3-2 \sqrt{3*5}+5=8-2 \sqrt{15} $$
е) (5 - √5)^2 + 5√5=$$ (25-10 \sqrt{5} +5)+5 \sqrt{5} = 30-5 \sqrt{5} $$

1) Разложите на множители с помощью формул сокращенного умножения выражение:
а) 49-k² а)64-с²
б)t²+2tx+x² б)а²-2ay+y²
в)m²-2m+1 в)z²+2z+1
2)Представьте в виде произведения выражения
а)25x²-10x+1 а)100k²-20²+1
б)64m²+16my+y² б)4х²+4xt+t²
3)Решите уравнение:
а) x²-10x+25=0 a)x²-18x+81=0
б)144x²-81=0 б)225x²-64=0
4)Разложите на множители многочлен
x³-y³+3x²+3xy+3y² x³+y³+2x²-2xy+2y²

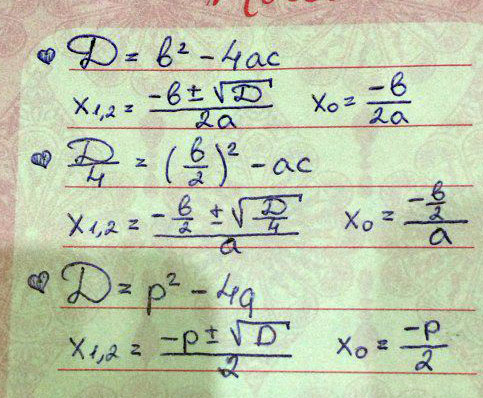
1) Разложите на множители с помощью формул сокращенного умножения выражение:
а) 49-k² а)64-с²
б)t²+2tx+x² б) а²-2ay+y²
в)m²-2m+1 в)z²+2z+1
2) Представьте в виде произведения выражения
а)25x²-10x+1 а)100k²-20²+1
б)64m²+16my+y² б)4х²+4xt+t²
3) Решите уравнение:
а) x²-10x+25=0 a)x²-18x+81=0
б)144x²-81=0 б)225x²-64=0