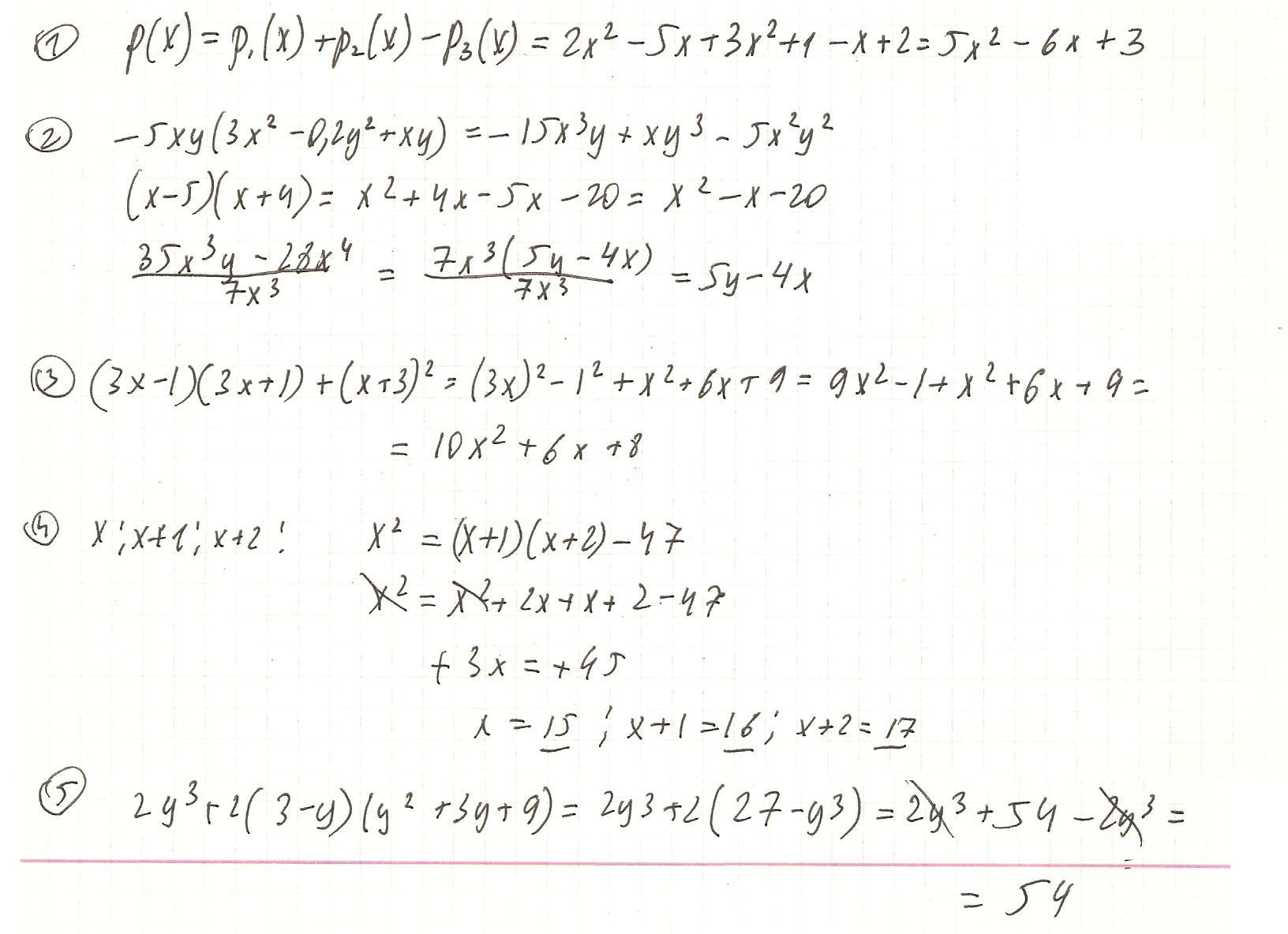преобразуйте выражения, используя формулы сокращенного умножения - страница 4
формулы сокращенного умножения сумма и разность кубов. Комбинации различных формул. 1) упростите выражение и найдите его значение : (5x+4)*(25x²-20x+16) ; при x=2. 2) преобразуйте в многочлен стандартного вида: (2x+1)²-(x-5)*(x+5) 3) решите равнение. (x-4)*(x+4)-6x=(x-2)² ²-это в квадрате, *-умножить.
Решение: 1)125х в 2 степени - 100 х в квадрате+ 80 х + 100 х в 2степени- 80х + 64. +80х и - 80 х сокращаются. 225х в 2 степени - 100 х в квадрате при х = 2225*4- 100*4=500
2) (2х+1)-(х-5)(х+5)=2х+1+х в квадрате- 25
3)(х-4)(х+4)-6х=(х-2) в квадрате =
х в квадрате - 16- 6х = х в квадрате - 4х +4
х в квадрате - х в квадрате - 6х +4х= 4+16
-2х=20
х=10
Составте многочлен р(х) и запишите его в стандартном виде, если р(х) = р1(х) + р2(х) – р3(х), где
р1(х) = 2х2 - 5х; р2(х) = 3х2 + 1; р3(х) = х – 2.
2 Преобразуйте выражение в многочлен стандартного вида:
а) -5ху(3х2 - 0,2у2 + ху); б) (х - 5)(х + 4); в) (35х3у - 28х4): 7х3.
3 Упростите выражение, применяя формулы сокращенного умножения:
(3х - 1)(3х + 1) + (х + 3)2
4 Найдите три последовательных натуральных числа, если известно, что квадрат меньшего из них на 47 меньше произведения двух других.
5 Докажите, что значение выражения 2у3 + 2(3 - у)(у2 + 3у + 9) не зависит от значения переменной.
Решение:1)p(x)=(2x^2-5x)+(3x^2+1)-(x-2)=5x^2-6x+3
2)
а) -5ху(3х^2 - 0,2у^2 + ху)=-15^3y+xy^3-5x^2y^2
б) (х - 5)(х + 4)=x^2+4x-5x-20=x^2-x-20
в) (35х^3у - 28х^4): 7х^3=(7x^3(5у - 4х): 7х^3=5y-4x
3) (3х - 1)(3х + 1) + (х + 3)^2=(3x)^2-1^2+x^2+6x+9=10x^2+6x+8
4)
x-1;x;x+1 -числа
(x-1)^2+47=x(x+1)
x^2-2x+1+47=x^2+x
-3x=-48
x=16 -второе число
x-1=16-1=15 -первое число
x+1=16+1=17 -третье число
5)
2у^3 + 2(3 - у)(у^2 + 3у + 9) =2y^3+(6-2y)(y^2+3y+9)=2y^3+(54-2y^3)=54
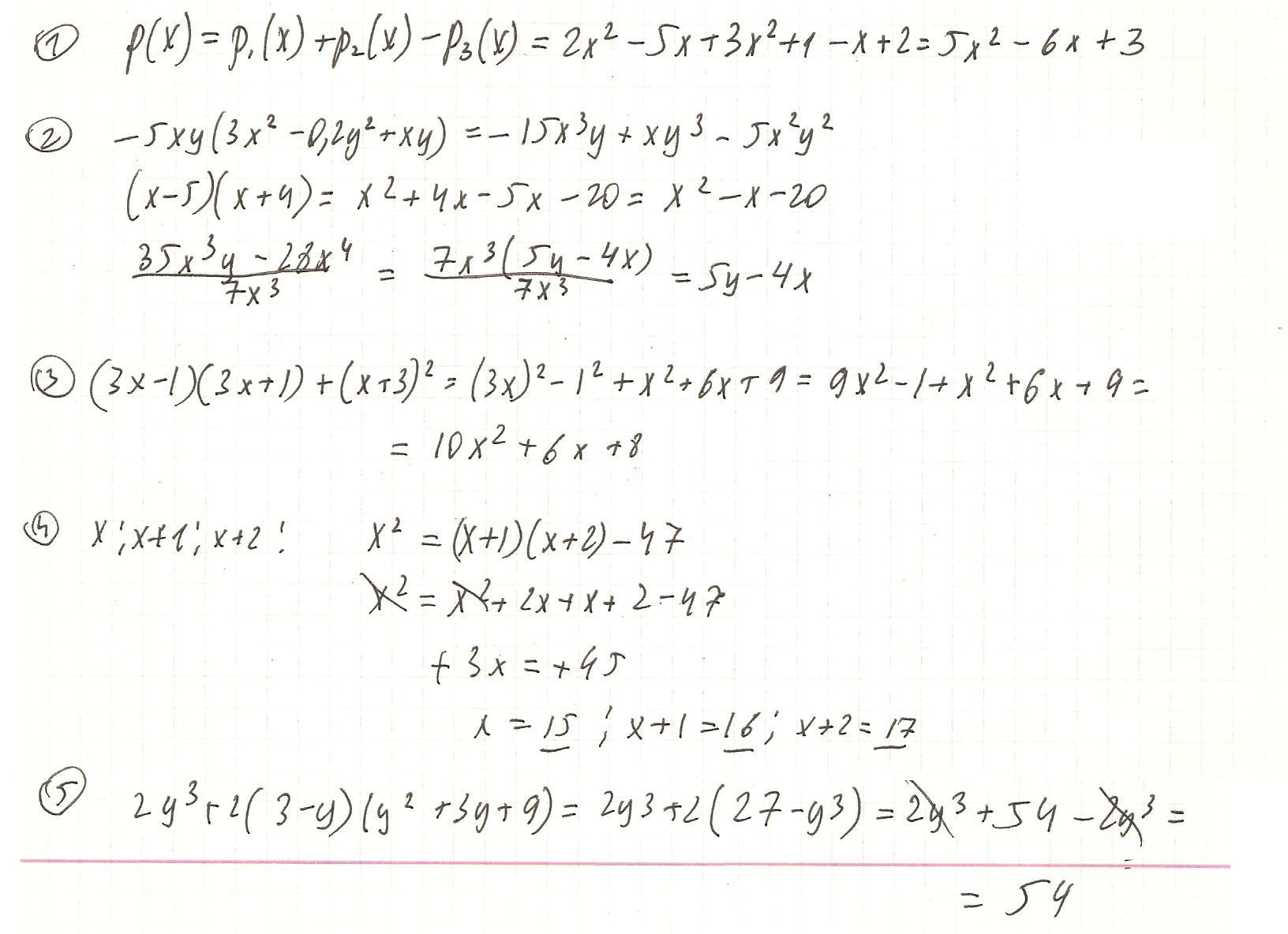
2. Преобразуйте заданное выражение в многочлен стандартного вида: а) 4xy(2x+0.5y -xy); б) (x-3)(x+2); в) (24x^2y+18x^3) : (-6x^2)
3. Упростите выражение, используя формулы сокращенного умножения: (2p-3)(2p+3) + (p-2)^2
5. Докажите, что значение выражения 5x^3 - 5(x+2)(x^2 - 2x +4)
^ перед степенью
Решение: 2) Преобразуйте заданное выражение в многочлен стандартного вида:а) $$ 4xy(2x+0.5y -xy)=8x^{2}y+2xy^{2}-4x^{2}y^{2} $$
б) $$ (x-3)(x+2)=x^{2}+2x-3x-6=x^{2}-x-6 $$
в) $$ (24x^2y+18x^3) : (-6x^2)=6x^2(4y+3x):(-6x^2)=-4y-3x $$
3) Упростите выражение, используя формулы сокращенного умножения:
$$ (2p-3)(2p+3) + (p-2)^2=(2p)^2-3^2+p^2-4p+4=5p^2-4p-5 $$
5) Докажите, что значение выражения:
$$ 5x^3 - 5(x+2)(x^2 - 2x +4) \ =5x^3-(5x+10)*(x^2-2x+4)=5x^3-(5x^3+40)=-40 $$
Если тебе не сложно поставь спасибо.
Вариант 4
1. Составьте многочлен p(x)=p1(x)+3p2(x)-p3(x) и запишите его в стандартном виде, если:
p1(x)=-7x^2+4
p2(x)=3x-2
p3(x)=-6x^2-3x
2. Преобразуйте заданное выражение в многочлен стандарстного вида:
а) -2/3 p^2g^2(6p^2-3/2pg+3g^2)
б) (2-3p)(p+3)
в) (-24pg^2+28p^2g)/(4pg)
3. Упрастите выражение, используя формулы сокращенного умножения:
(2+5y)(5y-2)-(4y-1)^2
4. Даны три последовательных числа, из которых каждое следующее на 6 больше предыдущего. Найдите эти числа, если произведение двух крайних чисел на 96 меньше произведения большего и среднего.
5. Докажите, что значение выражения
6(9x^3+2)-2(1-3x+9x^2)(1+3x)
не зависит от значения переменной.
Решение: 1.
$$ p(x)=p_1(x)+3p_2(x)-p_3(x) \\\ p(x)=-7x^2+4+3(3x-2)-(-6x^2-3x)= \\\ =-7x^2+4+9x-6+6x^2+3x=-x^2+12x-2 $$
2.
$$ - \frac{2}{3} p^2g^2(6p^2- \frac{3}{2}pg+3g^2)=- 4 p^4g^2+ p^3g^3- 2 p^2g^4 \\ (2-3p)(p+3)=2p+6-3p^2-9p=6-7p-3p^2 \\ \frac{-24pg^2+28p^2g}{4pg} =\frac{4pq(-6g+7p)}{4pg} =7p-6g $$
3.
$$ (2+5y)(5y-2)-(4y-1)^2=25y^2-4-(16y^2-8y+1)= \\\ =25y^2-4-16y^2+8y-1=9y^2+8y-5 $$
4.
Если х - второе число, то (х-6) - первое число, (х+6) - третье число. Составляем уравнение:
$$ (x-6)(x+6)=x(x+6)-96 \\\ x^2-36=x^2+6x-96 \\ 6x=60 \\\ x=10 \\\ x-6=10-6=4 \\\ x+6=10+6=16 $$
Ответ: 4, 10 и 16
5.
$$ 6(9x^3+2)-2(1-3x+9x^2)(1+3x)=54x^3+12-2(1+27x^3)= \\\ =54x^3+12-2-54x^3=10 $$
1) Преобразуйте данное целое выражение в произведение многочленов:
(x-1)(4x-6y)+(x+1)(18y-12x)
2) Разложите выражение на множители, используя формулы сокращенного умножения:
(a-b)^2-c^2
Решение: 1) (x-1)(4x-6y)+(x+1)(18y-12x)=(x-1)(4x-6y)+3(x+1)(6y-4x)=(6y-4x)(1-x+3(x+1))=
=2(3y-2x)(1-x+3x+3)=2(3y-2x)(4+2x)=4(3y-2x)(x+2)
2). (a-b)^2-c^2=(a-b+c)(a-b-c)
1 Преобразуйте
(Х-1)(4. х-6у)+(х+1)(18у-12х)=4х^2-4х-6ху+6у+18ху+18у-12х^2-12х=-8х^2-16х+12ху+24у=12у(х+2)-8х(х+2)=(х+2)(12у-8х)
2 разложите
(а-в)^2-с^2=(а-в+с)(а-в-с)