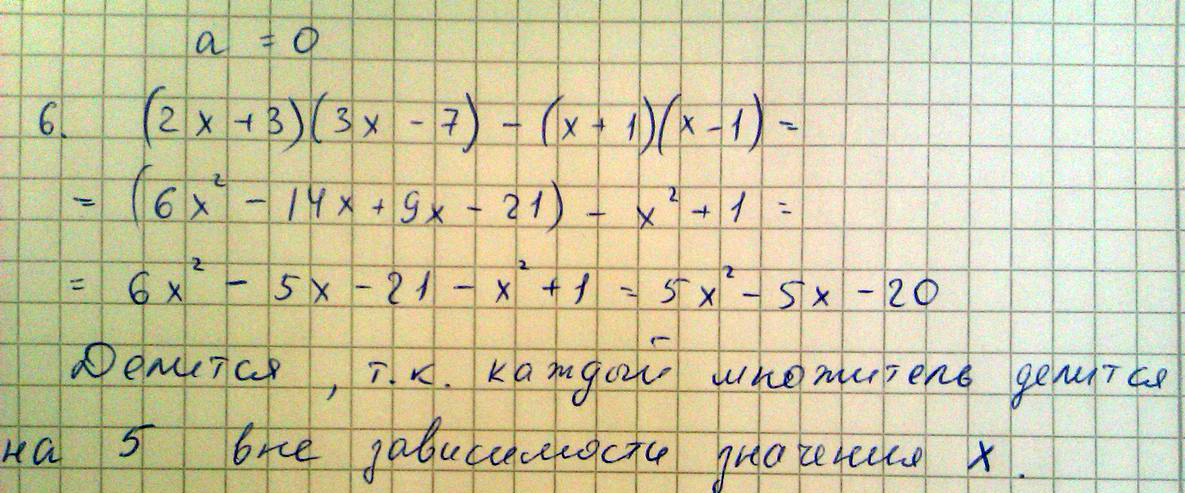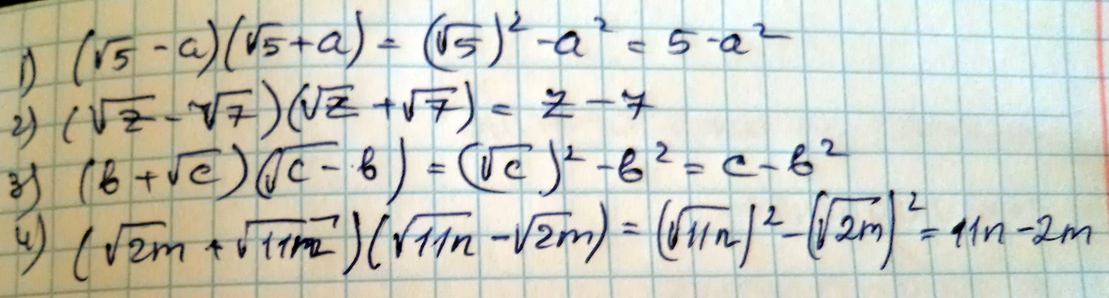упрощение выражений »

преобразуйте выражения, используя формулы сокращенного умножения - страница 5

  • Формулы сокращенного умножения
    1. Преобразуйте в многочлен:
    а) (х-4)² ;
    б) (3х-5) ² ;
    в) (2а-3)(2а+3) ;
    г) (у²-2)(у²+2 ).
    2. Разложите на множители:
    а) b²-0,36 ;
    б) y²-6y+9.
    3. Найдите значение выражения (2a-3b)3b+(a-3b)² при a=-2/7
    4. Выполните действия:
    а) 5(2-3xy)(2+3xy) ;
    б) (a³-b²)² ;
    в) (x+y)²-(x-y)².
    5. Решите уравнение (6a-1)(6a+1)-4a(9a+2)=-1.
    6. Делится ли на 5 выражение
    (2x+3)(3x-7)-(x+1)(x-1).
    при любом целом х?


    Решение: Вот несколько по максимуму, так что должно быть понятно. Можно использовать формулы сокр умножения, просто выучить их и все...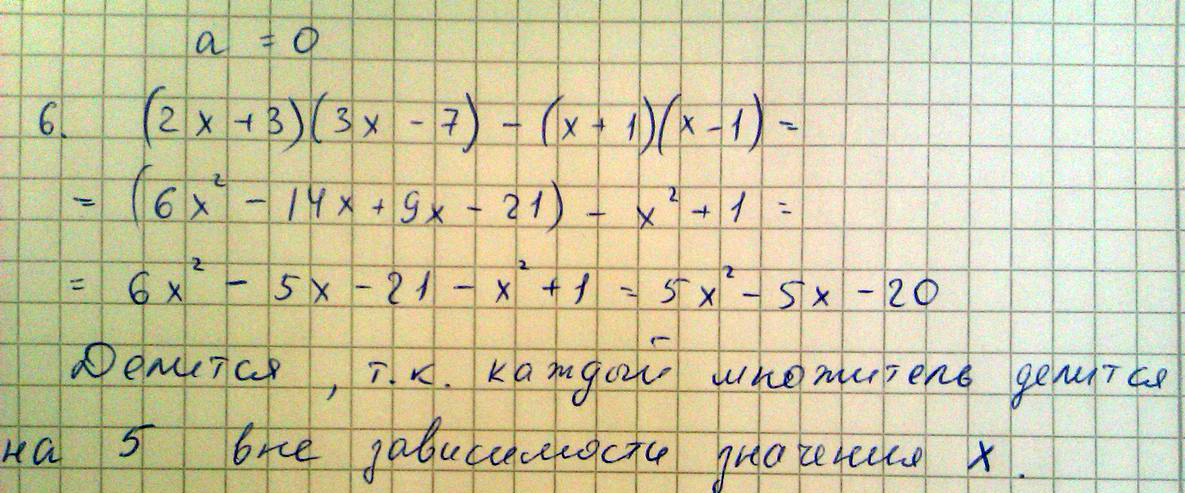Вот несколько по максимуму так что должно быть понятно. Можно использовать формулы сокр умножения просто выучить их и все......

  • Преобразуйте выражение используя формулы сокращенного умножение алгебра 8 класс


    Решение: Номер 89
    2)($$ \sqrt{p} $$ + 3$$ \sqrt{q} $$ $$ )^{2} $$ = p+6$$ \sqrt{pq} $$ + 9q
    4) (6$$ \sqrt{n} $$ + 7$$ \sqrt{m} $$ = 36n+ 84 $$ \sqrt{nm} $$ +49m
    Номер 91
    $$ \frac{3x+3 \sqrt{5} }{x+ \sqrt{5} } $$ = $$ \frac{3(x+ \sqrt{5} )}{x+ \sqrt{5} } $$ (x+$$ \sqrt{5} $$ сокращаете)

  • Преобразуйте выражение, используя формулы сокращенного умножения


    Решение:

    1) 5-а^2
    2) z-7
    3) в^2+c
    4) 2m+11n
    все по формуле (а+в)(а-в)= а^2-в^2

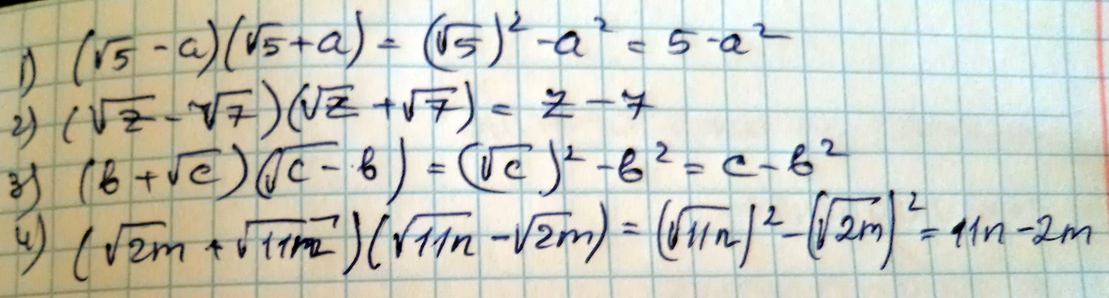
    -а z- в c m nвсе по формуле а в а-в а -в...

  • Преобразуйте выражение:
    а) (2х-5)^2= б)(3а+1\2b)=
    в)(а+4b)(2х+1\2а2)=
    г)(2х – 1\2 а^2)(2х+1\2а^2)=
    Разложите на множители:
    б)4а^2+20ab+25b^2
    в)4а^2^b2-25x^4
    Вычислите, используя формулы сокращённого умножения: а)212______________________
    б)19*21____________________
    в)482-472___________________
    г)1412-2*141*41+412__________


    Решение: а) (2х-5)^2=2x^2-20x+25

    б)(3а+1\2b)=0.5(6a+b)

    в)(а+4b)(2х+1\2а2)=2ax+8bx+0.5a^3+2a^2b=(2ax+0.5a^3)+(8bx+2a^2b)=0.5a(4x+a^2)+2b(4x+a^2)=(0.5a+2b)(4x+a^2)

    г)(2х – 1\2 а^2)(2х+1\2а^2)=4x^2-0.25a^4=0.25(16x^2-a^4)

    Разложите на множители:

    б)4а^2+20ab+25b^2=(2a+5b)^2=

    в)4а^2*b^2-25x^4=(2ab+5x^2)(2ab-5x^2)

    Вычислите, используя формулы сокращённого умножения:

    а)212

    б)19*21=399

    в)482-472=10

    г)141^2-2*141*41+41^2=(141-41)^2=100^2=10000

  • 1. Преобразуйте выражение:
    а) (m + n)²
    б) (a - 5)²
    в) (2 - 3у)²
    г) (b + 2)(b - 2)
    д) (4 - 5а)(5а + 4)
    е) (7х² - 6у)(7х² + 6у)
    2. Разложите на множители:
    а) а² - 9
    б) х² - 6х + 9
    в) 16 - 9у²
    г) 4х² + 4х + 1
    д) 36m⁴ - 25n²
    е) а⁴ - 16
    3. Решите уравнение:
    (3х - 1)(3х + 1) + (4х + 1)² = (5х -6)²
    4. Сторона первого квадрата на 1 см больше стороны второго квадрата, а площадь первого на 7 см² больше площади второго. Найдите сторону первого квадрата.
    5. Вычислите, используя формулы сокращённого умножения:
    а) 61² - 60²
    б) 73² + 2 · 73 · 27 + 27²
    в) 113² - 2 · 113 · 13 + 13²


    Решение: 1.
    (m+n)²=m²+2mn+n²
    (a-5)²=a²-10a+25
    (2-3y)²=4-12y+9y²
    (b+2)(b-2)=b²-4
    (4-5a)(5a+4)=(4-5a)(4+5a)=16-25a²
    (7x²-6y)(7x²+6y)=49x⁴-36y²
    2/
    a²-9=(a-3)(a+3)
    x²-6x+9=(x-3)²
    16-9y²=(4-3y)(4+3y)
    4x²+4x+1=(2x+1)²
    36m⁴-25n²=(6m-5n)(6m+5n)
    a⁴-16=(a²+4)(a²+4)
    3.
    (3x-1)(3x+1)+(4x+1)²=(5x+6)²
    9x²-1+16x²+8x+1=25x²+60x+36
    9x²+16x²-25x²+8x-60x-36=0
    - 52x=36
    x= - 36/52= - 9/13
    4.
    х (см)-сторона 1-го квадрата
    х+1 (см)-сторона 2-го квадр.
    S2 больше S1 на 7 см²
    (х+1)²-х²=7
    х²+2х+1-х²=7
    2х=7-1
    х=6:2
    х=3(см)-сторона 1-го квадрата
    5.
    61²-60²=(61-60)(61+60)=1*121=121
    73²+2*73*27+27²=(73+27)²=100²=10000
    113²-2*113*13+13²=(113-13)²=100²=10000

<< < 345 6 > >>