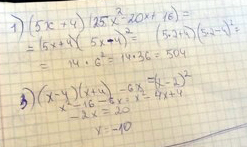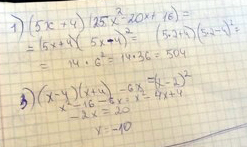упрощение выражений »
преобразуйте выражения, используя формулы сокращенного умножения - страница 3
2) Представьте в виде многочлена стандартного вида:
(5x - y)² - (y + 5x)²
3) Вычислите с помощью подходящих формул сокращённого умножения:
а) 7,2² ; б) 18³ ; в) 6,8² ; г) 31³
4) Преобразуйте в многочлен:
а) (x + 4m)² ; б) (3a - 4)³ ; в) (p² + 2q²r)² ; г) (x - 6m)² ; д) (5a + 2)³ е) (p³q - 3r²)³
Решение: 2) $$ (5x-y)^{2} - (y+5x)^{2} = 25x^{2}-10xy+ y^{2} - y^{2} -10xy-25 x^{2} = -20xy $$
3) $$ 7.2^{2} = (7+0.2)^{2} = 49+2.8+0.04=51.84 $$
$$ 18^{3} = (20-2)^{3}=8000 - 2400+ 240-8=5832 $$
$$ 6.8^{2} = (7-0.2)^{2} = 49-2.8+0.04=46.24 $$
$$ 31^{3} = (30+1)^{3}= 27000+2700+90+1= 29791 $$
4) $$ (x+4m)^{2} = x^{2} +8xm+ m^{2} $$
$$ (3a-4)^{3} = 27 a^{3}-108 a^{2} +144a - 64 $$
$$ ( p^{2}+2 q^{2}r) ^{2} = p^{4} +4 p^{2} q^{2}r+4 q^{4} r^{2} $$
$$ (x-6m)^{2}= x^{2} -12xm+36 m^{2} $$
$$ (5a+2)^{3} = 125 a^{3} +150 a^{2} +60a-8 $$
$$ ( p^{3}q - 3 r^{2} ) ^{3} = p^{9} q^{3}-9 p^{6}q2 r^{2} + 27 p^{3}q r^{2} -27 r^{6} $$1. преобразуйте квадрат двучлена в многочлен стандартного вида ; а) (-z - 3 ) во второй степени б) ( -n + 8 ) во второй степени в) ( - m - 10) во второй степени г) ( 2a + 1 ) во второй степени д) (3c-2) во второй степени е) (6х - 3 ) во второй степени ё) (7у + 6 ) во второй степени ж) (8х + 3у ) во второй степени з) ( 6m - 4n) во второй степени и)(9p - 2q) во второй степени к) (10z + 3t) во второй степени 2 задание используя формулы для (а +-b) вычислите ; а)79во второй степени б)39во второй степени в)59во второй степени г) 69 во второй степени д) 21во второй степени е)31во второй степени ё)61во второй степени ж) 91 во второй степени. 3. Выполните действие, используя соответствующую формулу сокращенного умножения: а) 3х - 5у)(3х + 5у) б)(7а-8b)(7a+8b) в)(5х-2у во второй степени)(5х+2у во второй степени) г) (2с-3а во второй степени)(3а+2с во второй степени)
Решение: 1 задание:а)(-z-3)^2=z^2+6z+9
б)(-n+8)^2=64-16n+n^2
в)(-m-10)^2=m^2+20m+100
г)(2a+1)^2=4a^2+4a+1
д)(3c-2)^2=9c^2-12c+4
е)(6x-3)^2=36x^2-36x+9
ё)(7y+6)^2=49y^2+84y+36
ж)(8x+3y)^2=64x^2+48xy+9y^2
з)(6m-4n)^2=36m^2-48mn+16n^2
и)(9p-2q)^2=81p^2-36pq+4q^2
к)(10z+3t)^2=100z^2+60zt+9t^2
3 задание
а)(3x-5y)(3x+5y)=9x^2-25y^2
б)(7а-8b)(7a+8b)=49a^2-64b^2
в)(5х-2y^2)(5x+2y^2)=25x^2-4y^4
1) используя формулу сокращенного умножения, вычислите: 86 в квадрате вычесть 14 в квадрате?
2) Разложите на множители многочлен: х в квадрате прибавить 2ху прибавить у в квадрате и вычесть 4?
3) разложите на множители выражение:(а в квадрате вычесть b в квадрате)-(а в квадрате вычесть 2аb прибавить b квадрат)
Решение: 1) 86²-14²=(86+14)(86-14)=100*72=7200
2) x²+2xy+y²-4=(x+y)²-2²=(x+y+2)(x+y-2)
3) (a²-b²)-(a²-2ab+b²)=(a+b)(a-b)-(a-b)²=(a-b)(a+b-(a-b))=(a-b)(a+b-a+b)=2b(a-b)Преобразуйте выражение в многочлен (правила сокращенного умножения):
а)(2q-2) во второй степени
б)(4x+y) во второй степени
в)(x+2/5y)(x-2/5y) во второй степени
Решение: $$A) (2q-2)^{2} = (2(q-1))^{2} = 4(q^{2} - 2q +1)=4 \\ q^{2} - 8q +4 \\ б) (4x+y)^{2} = (4x)^{2} + 2*4x*y + y^{2} = 16x^{2} + 8xy + y^{2} \\ в) ((x+2/5y)(x-2/5y))^{2} = (x^{2} - (2/5y)^{2})^{2} =\\= x^{4} - 2*x^{2}*(2/5y)^{2} + (2/5y)^{4} = x^{4} - 0,32x^{2}y^{2} + 0,16y^{4} $$формулы сокращенного умножения сумма и разность кубов. Комбинации
различных формул. 1) упростите выражение и найдите его значение :
(5x+4)*(25x²-20x+16) ; при x=2. 2) преобразуйте в многочлен стандартного
вида: (2x+1)²-(x-5)*(x+5) 3) решите равнение. (x-4)*(x+4)-6x=(x-2)² ²-это
в квадрате, *-умножить.
Решение: Вот первое и 3 задания:1) (5x+4)*(25x²-20x+16)=(5х+4)*(5х-4)=25х²-16
25*2²-16=84
2) (2x+1)²-(x-5)*(x+5)=(4х²+4х+1)-(х²-25) или (2x+1)²-(х²-25)
3) (x-4)*(x+4)-6x=(x-2)²
(х²-16)-6х=х²-4х+4
х²-16-6х=х²-4х+4
х²-х²-6х+4х=4+16
-2х=20
х=20:(-2)
х=-10