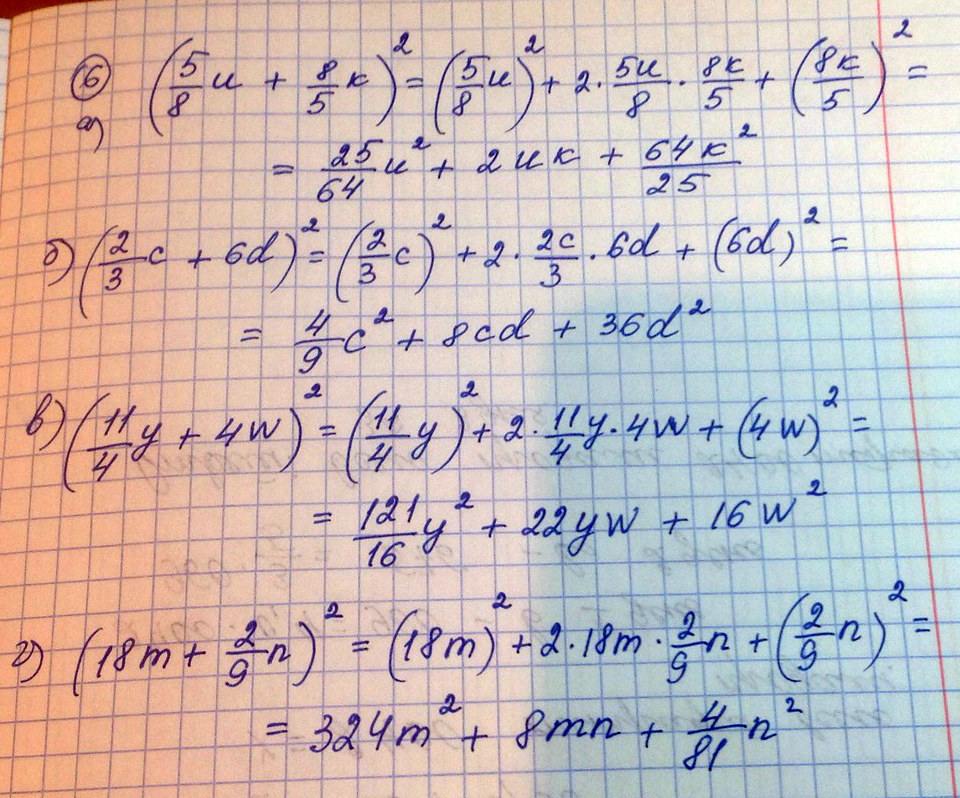преобразуйте выражение - страница 2
Преобразуйте выражение и вычислите его значение:
1) 58+79+12+21;
2) 20·17·5·3.
2. Вычислите, используя распределительное свойство:
1) 34·7 + 16·7;
2) 74
2
- 74·64;
3) 12·32 - 12·18 + 38·14.
3. Чтобы приготовить фасолевый салат, на 7 частей фасоли берут 4 части курицы и 2 части сыра.
1) Сколько сыра надо взять, чтобы приготовить 650г салата?
2) Сколько фасоли надо взять, если для салата имеется 360г курицы?
4. Альбом для рисования дороже карандаша в 10 раз, а вместе они стоят 275р. Сколько стоит
карандаш?
5. В двух ящиках 62 лимона, причем в первом на 12 лимонов больше, чем во втором. Сколько
лимонов в каждом ящике?
6. Кабачок легче тыквы на 1кг 800г, а их общая масса 3кг. Найти массу тыквы
Решение: 1.(58+12)+(79+21)=70+100=170
(20×5)×17×3=100×17×3=5100
4. Пусть х-стоимость карандаша.
Тогда 10х-стоимость альбома.
10х+х-общая стоимость альбома и карандаша.
В условии задачи известно, что общая стоимость альбома и карандаша составляет 275 рублей.
Составим уравнение:
10х+х=275
11х=275
х=275:11
х=25
Ответ: карандаш стоит 25 рублей.
5. Пусть х лимонов во втором ящике.
Тогда 12+х лимонов в первом ящике.
12+х+х лимонов в двух ящиках.
В условии задачи известно, что в двух ящиках 62 лимона.
Составим уравнение:
12+х+х=62
12+2х=62
2х=62-12
2х=50
х=50:2
х=25
25 лимонов во втором ящике.
2)25+12=37(л.)-в первом ящике.
Ответ:25 лимонов,37 лимонов.
Преобразуйте выражения, используя законы умножения: 0,4а(-5b) (2х-1)(-0,2) 3(-х-1) -0,2х(-5у) (-2х-4). 0,1 -5(2-х)
Решение: $$ 0,4a(-5b)=-2ab\\\\ \\ (2x-1)(-0,2)=-0,4x+0,2\\\\ \\ 3(-x-1) =-3x-3\\\\\\-0,2x(-5y)=xy\\\\ \\ (-2x-4)\cdot 0,1=-0,2x-0,4\\\\ \\ -5(2-x)=-10+x $$1. 0,4a(-5b) = 0,4 × (-5) × a × b = -2ab
2. (2x - 1)(-0,2) = 2x × (-0,2) -1 × (-0,2) = -0,4x + 0,2
3. 3(-x - 1) = 3 × (-x) + 3 × (-1) = -3x - 3
4.0,2x(-5y) = -0,2 × (-5) × x × y = 1xy = xy
5. 0,1(-2x - 4) = 0,1 × (-2x) + 0,1 × (-4) = -0,2x - 0,4
6.5(2 - x) = -5 × 2 - 5 × (-x) = -10 + 5x = 5x - 10
№6) С помощью формулы квадрата суммы преобразуйте выражение в многочлен :
а) (5/8u + 8/5k)²
б) (2/3c +6d)²
в) (11/4y + 4w)²
г) (18m + 2/9n)²
№7) С помощью формулы квадрата разности преобразуйте выражение в многочлен:
а) (k - 8)²
б) (5 - 7m)²
в) (13p - 3)²
г) (5v - 5)²
№8) С помощью формулы квадрата разности преобразуйте выражение в многочлен:
а) (2h - 1/4)²
б) (10d - 1/5)²
в) (4/3y - 9/8)²
г)(3m - 2/3)²
Решение:а) (5/8u + 8/5k)²=25/64u²+2uk+64/25k²
б) (2/3c +6d)²=4/9c²+8cd+36d²
в) (11/4y + 4w)²=121/16y²+22yw+16w²
г) (18m + 2/9n)²=324m²+8mn+4/81n²
а) (k - 8)²=k²-16k+64
б) (5 - 7m)²=25-70m+49m²
в) (13p - 3)²=169p²-78p+9
г) (5v - 5)²=25v²-50v+25
а) (2h - 1/4)²=4h²-h+1/16
б) (10d - 1/5)²=100d²-4d+1/25
в) (4/3y - 9/8)²=16/9y²-3y+81/64
г)(3m - 2/3)² =9m²-4m+4/9
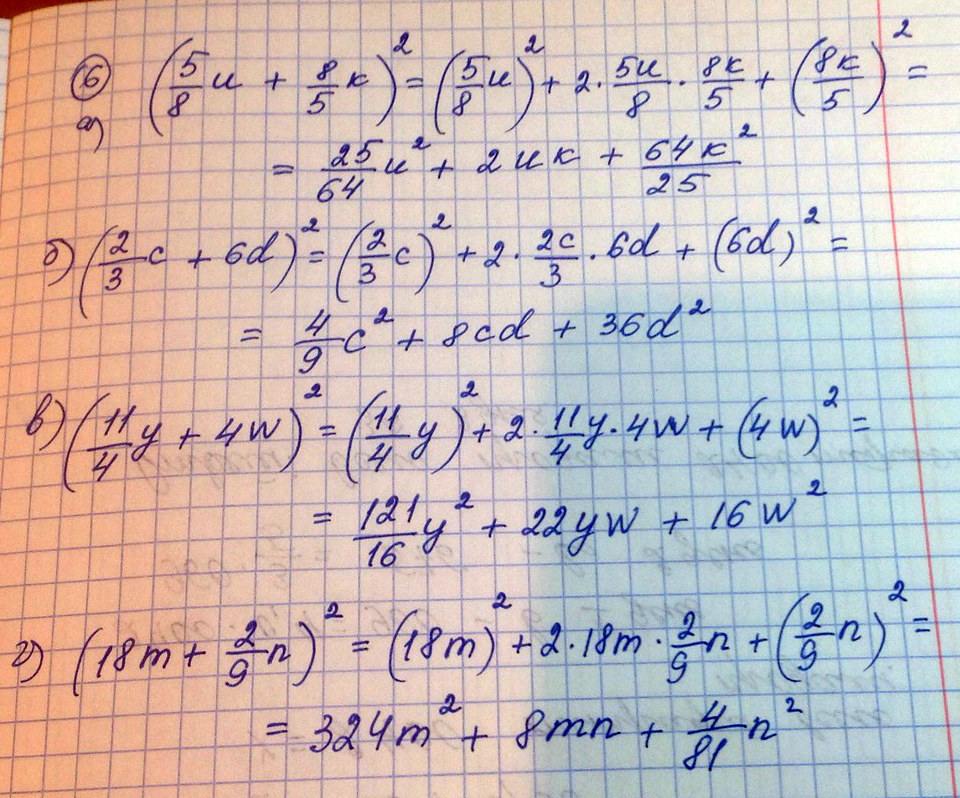
4х-3х(х+1)=.
(х+4)(-х+2)=.
Преобразуйте выражение, используя формулы сокращенного умножения.
(1-b)(1+b)=.
(10p+7q)(7q-10p)=.
(x-8) в квадрате.=.
(9p-7q) в квадрате. =.
(x+1)(x в квадрате. x + 1)=.
Решение: 4х-3х(х+1)= 4х-3х^2 - 3х = х - 3х^2(1-b)(1+b)= 1-b^2
(10p+7q)(7q-10p)= (7q+10p)(7q-10p)=49q^2 + 100p^2.
(x-8)^2 = х^2 - 2*х8 + 64
(9p-7q)^2 = 81р^2 - 2*(9р*7q ) - 49q
Преобразуйте выражение в тождественно равное выражение
3(a+4)+4(a-3); 2(b+7)-3(b+1); 8(c-3)+5(c+4); 2,4(d+1)-0,6(4d-3);
Решение: Исходя из классического определения распределительного свойства умножения, которое, в случае сложения, гласит “чтобы умножить число на сумму двух чисел, можно это число умножить на каждое слагаемое и полученные результаты сложить”, а в случае вычитания - “чтобы умножить число на разность двух чисел, можно умножить это число на уменьшаемое и на вычитаемое, и из первого произведения вычесть второе” преобразование заданных выражений будет иметь вид:
3(a+4) + 4(a-3) = (3a+3*4) + (4a+4*(-12))= 3a+12+4a-12 = 7a;
2(b+7) - 3(b+1) = (2b+2*7) - (3b+3*1)=2b+14-3b-3 = 11 - b;
8(c-3) + 5(c+4) = (8c-8*3) + (5c+5*4)=8c-24 + 5c+20 = 13c - 4;
2,4(d+1) - 0,6(4d-3) = (2,4d+2,4*1)-(0,6*4d-0,6*3)=2,4d+2,4-2,4d+1,8 = 4,2 (d сократилось).