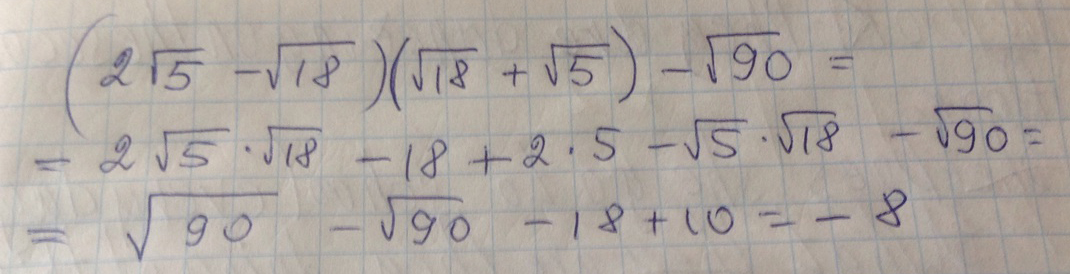упрощение выражений »
преобразуйте выражение - страница 4
Преобразуйте выражение \((-\frac{2}{3}a^{-4}b^{-8})^{-2}\cdot(3a^2b^{12})^{-3}\) так, чтобы оно не содержало степеней с отрицательным показателем.
Решение: $$ (-\frac{2}{3}a^{-4}b^{-8})^{-2}\cdot(3a^2b^{12})^{-3} = \\\\ =(-\frac{2}{3})^{-2}a^8b^{16}3^{-3}a^{-6}b^{-36} = \frac{9}{4}\frac{1}{27}a^2/b^{20} = \frac{a^2}{12b^{20}} $$(-2/3 а⁻⁴b⁻⁸) ⁻² * ( 3a² b¹² )⁻³ = ((-2/3)⁻² a⁸ b¹⁶) * (3⁻³a⁻⁶b⁻³⁶) =
a²
= 9/4*a⁸⁻⁶ b¹⁶⁻³⁶ * (1/27) = 1/12 a² b⁻²⁰= -
12b²⁰Преобразуйте выражение к виду \( \sqrt[n]{x} \\ \sqrt{2m \sqrt[3]{ \frac{1}{4 m^{2} } \sqrt{ \frac{n}{m} } } } : \sqrt[12]{nm} \)
Решение: $$ \sqrt{2m \sqrt[3]{\frac{1}{4m^2} \sqrt{\frac{n}{n}}} }: \sqrt[12]{nm} = \sqrt{2m\left (\frac{1}{4m^2}\cdot (\frac{n}{m})^{\frac{1}{2}}\right )^{\frac{1}{3}}} :(nm)^{\frac{1}{12}}=\\\\=\sqrt{\frac{2m\cdot n^{\frac{1}{6}}}{2^{\frac{2}{3}}\cdot m^\frac{2}{3}\cdot m^{\frac{1}{6}}}}:(nm)^{\frac{1}{12}}=\sqrt{ \frac{2^{\frac{1}{3}}\cdot m^\frac{1}{3}n^{\frac{1}{6}}}{m^{\frac{1}{6}}}}:(nm)^{\frac{1}{12}}= $$
$$ =\left(2^{\frac{1}{3}}\cdot m^{\frac{1}{6}}\cdot n^{\frac{1}{6}}\right )^{\frac{1}{2}}:(nm)^{\frac{1}{12}}= $$ $$ \frac{2^{\frac{1}{6}}\cdot (nm)^{\frac{1}{12}}}{(nm)^{\frac{1}{12}}}=2^{\frac{1}{6}}=\sqrt[6]{2} $$Преобразуйте выражение:
(2√5-√18)(√18+√5)-√90
Решение: Ответ -82√5=√20
√20*√18+√20*√5-√18*√18-√18*√5-√90=
√360+√100-18-√90-√90=
6√10+10-18-2√90=6√10-8-6√10=-8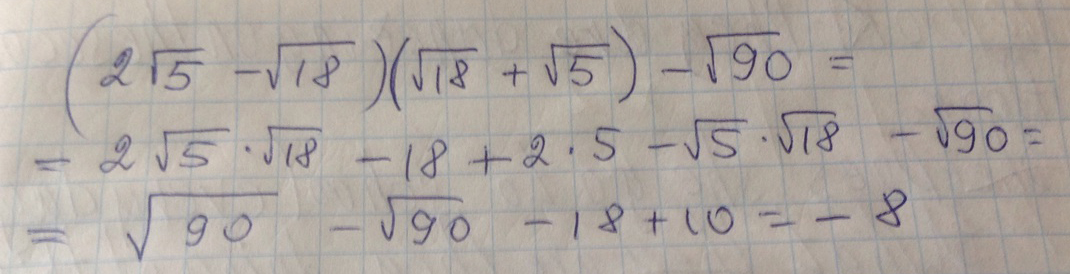
преобразуйте выражение в дробь: 2
m m
______ - ___
2
m - 16 m+4
Решение: 2
m - 16=(m-4)(m+4)домножаем вторую дробь на (m-4)
получаем
2 2 2
m - m( m-4) m - m +4m___________ = ________________ = 4m/(m-4)(m+4)
(m-4)(m+4) (m-4)(m+4)
Преобразуйте выражение 5sinx+12cosx к виду C sin(x+t) или С cos (x+t)
Решение: $$ f(x)=5sinx+12cosx\\\\5^2+12^2=25+144=169=13^2\\\\f(x)=5sinx+12cosx=[\frac{\cdot 13}{\cdot 13}]=13\cdot (\frac{5}{13}sinx+\frac{12}{13}cosx)\\\\(\frac{5}{13})^2+(\frac{12}{13})^2=\frac{25+144}{169}=\frac{169}{169}=1\; \; \Rightarrow \; \; \frac{5}{13}=cos \alpha,\; \frac{12}{13}=sin \alpha \;,\; tak\; kak\\\\sin^2 \alpha +cos^2 \alpha =1\\\\tg \alpha =\frac{sin \alpha }{cos \alpha }=\frac{12}{5}\\\\f(x)=13\cdot (cos \alpha \cdot sinx+sin \alpha \cdot cosx)=13\cdot sin(x+ \alpha ), $$
где $$ tg \alpha =\frac{12}{5} $$, $$ \alpha =arctg\frac{12}{5}. $$