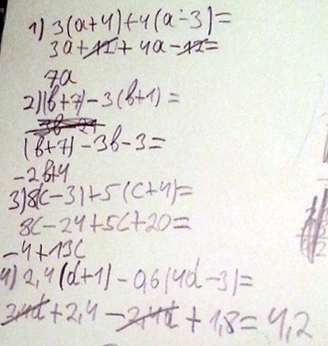упрощение выражений »
преобразуйте выражение - страница 3
Преобразуйте выражение в тождественно равное выражение:
3(a+4)+4(a-3)
2(b+7)-3(b+1)
8(c-3)+5(c+4)
2.4(d+1)-0.6(4d-3)
Решение: 3(a+4)+4(a-3)=3а+12+4а-12=7а
2(b+7)-3(b+1)=2b+14-3b-3=-b+11
8(c-3)+5(c+4)=8c-24+5c+20=13c-4
2.4(d+1)-0.6(4d-3)=2,4d+2,4-2,4d+1,8= 4,2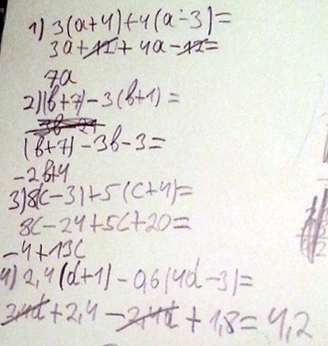
Преобразуйте выражение в тождественно равное, используя распределительное свойство умножения.
9(2+m)
-3(1,5+n)
2,8(3-m)
-1,5(2-n)
Решение: Исходя из классического определения распределительного свойства умножения, которое, в случае сложения, гласит “чтобы умножить число на сумму двух чисел, можно это число умножить на каждое слагаемое и полученные результаты сложить”, а в случае вычитания - “чтобы умножить число на разность двух чисел, можно умножить это число на уменьшаемое и на вычитаемое, и из первого произведения вычесть второе” преобразование заданных выражений будет иметь вид:
1) 9*(2 + m) = 9*2 + 9*m = 18 + 9m;
2) -3*(1,5 + n) = (-3)*1,5 + (-3)*n = -4,5 - 3n;
3) 2,8*(3 - m) = 2,8*3 - 2.8*m = 8,4 - 2,8m;
4) -1,5*(2 - n) = -1,5*2 - (-1,5)*n = -3 + 1,5m = 1,5m - 3.Преобразуйте выражение в произведение :
Cosb-sin6b
Решение:
$$ \cos{b} - \sin{6b} = \cos{b} + \sin{ ( -6b ) } = \\\\ = \cos{b} + \cos{ ( \frac{ \pi }{2} - [-6b] ) } = \cos{b} + \cos{ ( \frac{ \pi }{2} + 6b ) } \ ; $$
Воспользуемся формулой: $$ \cos{x} + \cos{y} = 2 \cos{ \frac{x+y}{2} } \cos{ \frac{x-y}{2} } \ ; \\ \cos{b} - \sin{6b} = \cos{b} + \cos{ ( 6b + \frac{ \pi }{2} ) } = 2 \cos{ \frac{ b + 6b + \pi/2 }{2} } \cos{ \frac{ b - 6b - \pi/2 }{2} } = \\\\ = 2 \cos{ \frac{ 7b + \pi/2 }{2} } \cos{ \frac{ 5b + \pi/2 }{2} } = 2 \cos{ ( 3.5b + \frac{ \pi }{4} ) } \cos{ ( 2.5b + \frac{ \pi }{4} ) } \ ; $$
О т в е т : $$ \cos{b} - \sin{6b} = 2 \cos{ ( 3.5b + \frac{ \pi }{4} ) } \cos{ ( 2.5b + \frac{ \pi }{4} ) } \. $$
Преобразуйте выражение в тригонометрические функции от угла альфа: Cos (3П\2+альфа) и sin (П- альфа). в) tg (П\2+альфа)
Решение: Про формулам приведения:
cos ((3π/2)+α) = sinα
Так как прибавляется нечетное число
3·(π/2), то название приведенной функции меняется на кофункцию
косинус сменился на синус.
угол ((3π/2)+α) в 4-ой четверти, знак косинуса в 4 четверти +, поэтому перед синусом ставим +, ничего не пишем.
sin (π- α)=sinα
так как прибавляется четное число
2·(π/2)=π, то название приведенной функции не меняется, остается справа синус.
угол (π-α) во 2-ой четверти, знак синуса во 2 четверти +, поэтому перед синусом ставим +, ничего не пишем.
tg ((π/2)+α)= - ctgα
Так как прибавляется четное число
1·(π/2), то название приведенной функции меняется на кофункцию
тангенс сменился на котангенс.
угол ((π/2)+α) во 2-ой четверти, знак тангенса во 2-й четверти - поэтому перед котангенсом ставим -
Преобразуйте выражение в одночлен стандартного вида (покажите сам процесс): (-3a^7b^2)^4×1/27×ab
Решение: (-3a^7b^2)^4*1/27*ab=(-3)^4*a^(7*4)*b^(2*4)*(1/3^3)*a*b =(-3)^4*a^28*b^8*(1/3^3)*ab = 3a^29*b^9здесь главное все разложить по полочкам, когда ты какое либо число/букву в степени возводите еще в степень, то степени перемножаются,1/27 можно представить как 1/3^3
и когда ты делите 3^4 на 3^3, то из степени 4 вычитаете степень 3, то есть из степени числителя вычитаете степень знаменателя