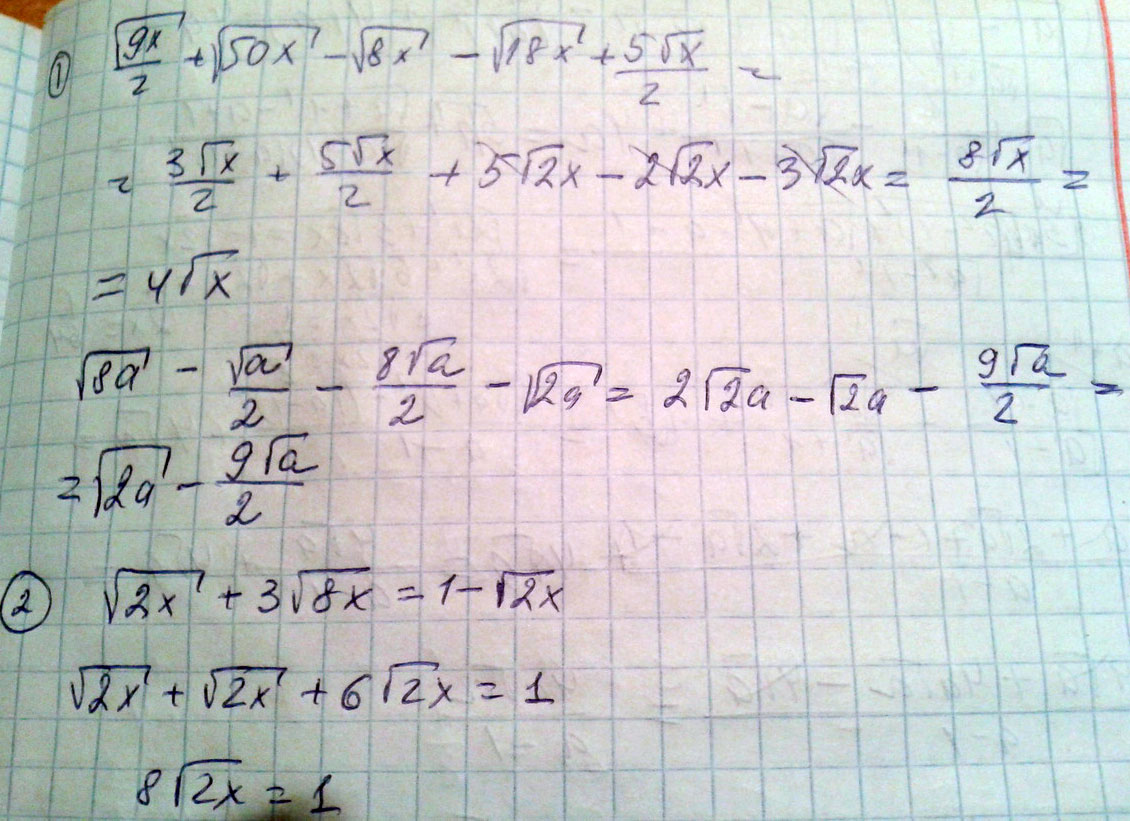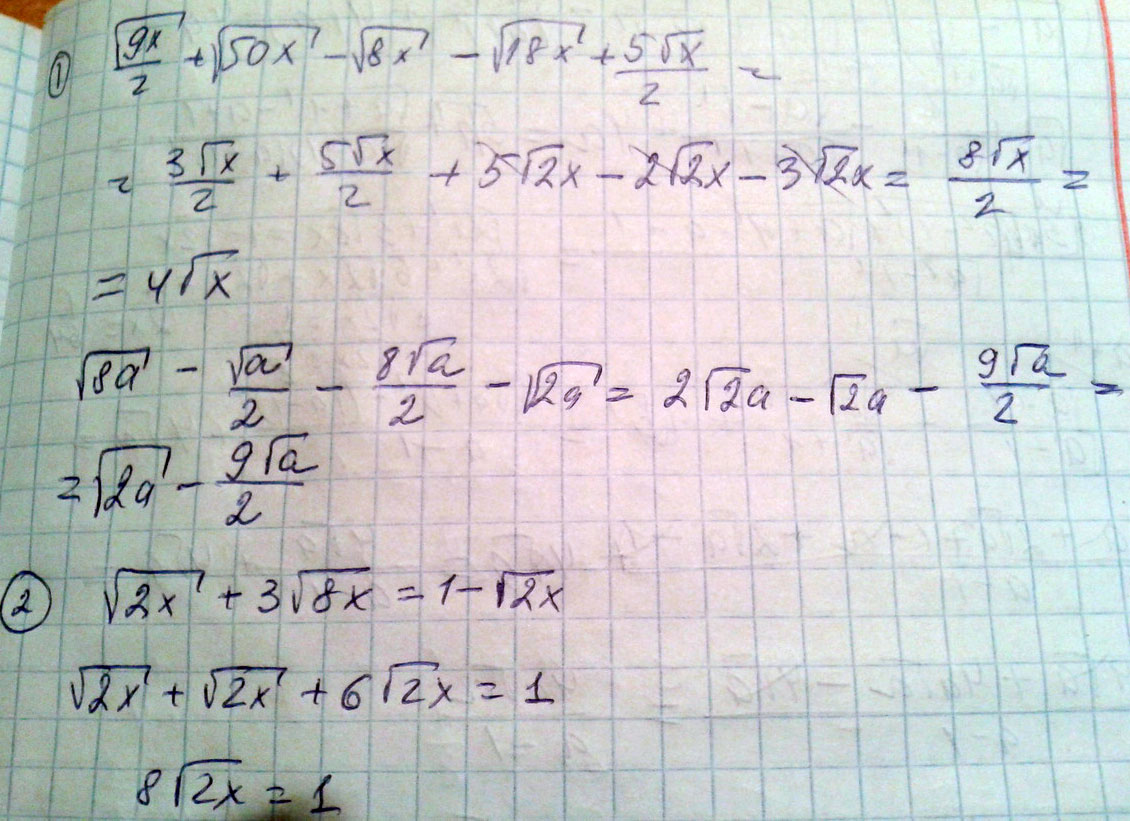упростите выражение - страница 9
Сократите дробь: а)36-а/6-√а б)5-√5/√15-√3 освободитесь от знака корня в знаменателе: а)15/√5 б)5/√13 - √3 докажите что значение выражения 4/2√3 - 1 - 4/2√3 - 1 является рациональным числом. упростите выражение а)√х в шестой степени
Решение: Сократите дробь:а)(36-а)/(6-√а)=((6-√а)(6+√а))/(6-√а)=(6+√а)б)(5-√5)/(√15-√3)=(√5(√5-1))/(√3(√5-1))= √(5/3)
освободитесь от знака корня в знаменателе: а)15/√5
15=√5*√5*3,соответственно 15/√5=(√5*√5*3)/√5=3√5
б)5/(√13 - √3) здесь используется метод домножения на сопряженное, соответственно:
5/(√13 - √3) =5(√13 + √3) /(13-3)=(√13 + √3)/2
докажите что значение выражения 4/2√3 - 1 - 4/2√3 - 1 является рациональным числом:
4/2√3 - 1 - 4/2√3 - 1 это выражение равно -2, так как если мы переставим слагаемые по-другому,получим:
4/2√3 - 4/2√3 -1 -1, отсюда видно что:
4/2√3 - 1 - 4/2√3 - 1= -2
упростите выражение а)√х в шестой степени = х^3 так как √х^6= x^(6/2) и соответственно это x^3
Упростите выражение. t^7*t^4*t
t^15:t^5
(t^9)^3
Решение:$$ a) t^7\cdot t^4\cdot t=t^{7+4+1}=t^{12} \\b)\;t^{15}:t^5=t^{15-5}=t^{10} \\c) (t^9)^3=t^{9\cdot3}=t^{27} $$
При возведении степени в степень показатели перемножаются, при перемножении подстепенных выражений степени складываются.
При умножении одинаковых чисел с разными степенями, степени складываются, при делении - отнимаются, при возведении в степень - перемножаются.
а)
$$ t^7*t^4*t^1=t^{7+4+1}=t^{12} $$
б)
$$ t^{15}:t^5=t^{15-5}=t^{10} $$
в)
$$ (t^9)^3=t^{9*3}=t^{27} $$
Упростите выражение:а.(m-2)все это в квадрате -(m+1)(m-3)
б.5(d-c)всё это в квадрате+10dc
в.х в третьей степени+(2-х)(х в квадрате +2х+4)
Решение: a) Выражение: (m-2)^2-(m+1)*(m-3)
Решаем по шагам:
1. m^2-4*m+4-(m+1)*(m-3)
2. m^2-4*m+4-(m^2-2*m-3)
3. m^2-4*m+4-m^2+2*m+3
4. -4*m+4+2*m+3
5. -2*m+4+3
6. -2*m+7
Ответ: 7-2*m
b) Выражение: 5*(d-c)^2+10*d*c
Решаем по шагам:
1. 5*(d^2-2*d*c+c^2)+10*d*c
2. 5*d^2-10*d*c+5*c^2+10*d*c
3. 5*d^2+5*c^2
Ответ: 5*d^2+5*c^2
Выражение: x^3+(2-x)*(x^2+2*x+4)
Решаем по шагам:
1. x^3+8-x^3
2. (2-x)*(x^2+2*x+4)=8-x^3
Ответ: 8
(^-степень, *-умножение)Упростите выражения: \( \frac{\sin^2 \alpha }{1+\cos \alpha } \)
\( \frac{\cos^2 \alpha }{1-\sin \alpha }\)
\( 1-\cos^2 \alpha -\sin^2 \alpha \)
\( (1+tg^2 \alpha )\cdot\cos^2 \alpha \)
\( (tg \alpha +ctg \alpha )^2-(tg \alpha -ctg \alpha )^2\)
Решение: $$ \frac{\sin^2 \alpha }{1+\cos \alpha } = \frac{1-\cos^2 \alpha }{1+\cos \alpha } = \frac{(1-\cos \alpha)(1+\cos \alpha) }{1+\cos \alpha } =1-\cos \alpha \\ \frac{\cos^2 \alpha }{1-\sin \alpha } = \frac{1-\sin^2 \alpha }{1-\sin \alpha } = \frac{(1-\sin \alpha)(1+\sin \alpha) }{1-\sin \alpha } = 1+\sin \alpha \\ 1-\cos^2 \alpha -\sin^2 \alpha =1-(\cos^2 \alpha+\sin^2 \alpha) =1-1=0 \\ (1+tg^2 \alpha )\cdot\cos^2 \alpha = \frac{1}{ \cos^2 \alpha }\cdot \cos^2 \alpha =1 \\ (tg \alpha +ctg \alpha )^2-(tg \alpha -ctg \alpha )^2= \\\ =tg^2 \alpha +2tg\alpha ctg \alpha+ ctg^2 \alpha-(tg^2 \alpha -2tg\alpha ctg \alpha+ ctg^2 \alpha)= \\\ =tg^2 \alpha +2tg\alpha ctg \alpha+ ctg^2 \alpha-tg^2 \alpha +2tg\alpha ctg \alpha- ctg^2 \alpha= \\\ =4tg\alpha ctg \alpha=4\cdot1=4 $$
Учитывая основное тригонометрическое тождество:
$$ \sin^4 \alpha -\cos^ 4\alpha =(\sin^2 \alpha -\cos^ 2\alpha )(\sin^2 \alpha +\cos^ 2\alpha )= \sin^2 \alpha -\cos^ 2\alpha $$
Учитывая основное свойство пропорции:
$$ (1+\cos \alpha )(1-\cos \alpha)=1-\cos ^2\alpha=\sin^2 \alpha $$
Упростите выражение:
1. (√8а - √а/2) - (8√а/2 + √2а)
2.(√9х/2 + √50х - √8х) - (√18х - 5√х/2)
Решите уравнение:
1. √2х + 3√8х=1 - √2х
Решение: Решаем исходя из того, что под корнем только числитель - 9х.