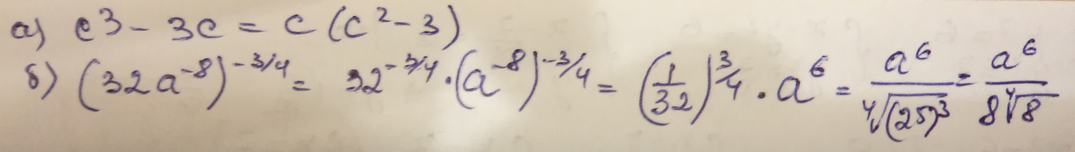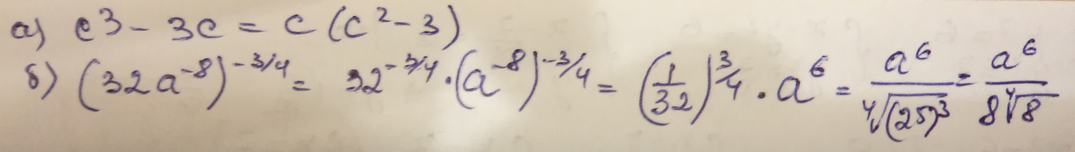выполните преобразование
1) Раскройте скобки и представьте в виде многочлена стандартного вида: (3x-1)(x+2) 2) у какого члена многочлена полученного при умножении многочленов (x^4+x^2+1)(x-2-3x^2) наибольшая степень относительно x 3)решите уравнение (3x^2+6x+4)-3(x^2+x+1)=0 4) не выполняя умножения назовите число членов многочлена который получиться при умножении (a+b+c)(m-n-p) 5)не выполняя умножения многочленов (x+3)(x+2)-x^2 скажите сколько членов будет иметь многочлен полученный при его преобразовании в многочлен стандартного вида
Решение: 1) (3x-1)(x+2) = 3x^2+6x-x-2=3x^2+5x-22) (x^4+x^2+1)(x-2-3x^2) = x^5-2x^4-3x^6+2x^3-x^2-3x^4+x-2-3x^2. У члена х^5 наибольшая степень относительно х
3) (3x^2+6x+4)-3(x^2+x+1)=0
3x^2+6x+4-3x^2-3x-3=0
3x+1=0
3x=-1
x=-1/3
Ответ: -1/3
4)Чтобы найти кол-во получившихся членов многочленов надо перемножить кол-во членов в 2 скобках. 3*3=9
Ответ;9
Вычислите рациональным способом. Укажите законы сложения, на основании которых выполнены тождественные преобразования: (10109+703)+(1397+9891)?
Решение: (10109+703)+(1397+9891) = (первое слагаемое с четвертым )+(второе слагаемое с третьим) = (10109 +9891)+(703+1397) = 20000 + 2100 = 22100
(10109+703)+(1397+9891) = / скобки раскрываем, знаки сохраняем / =
= 10109+703+1397+9891 = / от перемены мест слагаемых, сумма НЕ меняется/ =
= (10109+9891)+(703+1397) =20000+2100=221001) раскройте скобки и представьте в виде многочлена стандартного вида: (3x-1)(x+2)
2) у какого члена многочлена полученного при умножении многочленов (x^4+x^2+1)(x-2-3x^2) наибольшая степень относительно x
3) решите уравнение (3x^2+6x+4)-3(x^2+x+1)=0
4) не выполняя умножения назовите число членов многочлена который получиться при умножении (a+b+c)(m-n-p)
5) не выполняя умножения многочленов (x+3)(x+2)-x^2 скажите сколько членов будет иметь многочлен полученный при его преобразовании в многочлен стандартного вида
Решение: 1) (3x-1)(x+2) = 3x^2+6x-x-2=3x^2+5x-22) (x^4+x^2+1)(x-2-3x^2) = x^5-2x^4-3x^6+2x^3-x^2-3x^4+x-2-3x^2. У члена х^5 наибольшая степень относительно х
3) (3x^2+6x+4)-3(x^2+x+1)=0
3x^2+6x+4-3x^2-3x-3=0
3x+1=0
3x=-1
x=-1/3
Ответ: -1/3
4) Чтобы найти кол-во получившихся членов многочленов надо перемножить кол-во членов в 2 скобках. 3*3=9
Ответ;9
Преобразуйте в многочлен: а) а"2+(3а-b)ֶ б)(8x-y)ֶ-64xֶ в)2(a-b)ֶ г)-y(3x-y)ֶ Вынесите за скобки: а)(x-3)-y(x-3) б)x-p+(p-x)c Выполните преобразование по соответствующей формуле: а)(cֶ-1)ֶ б)(xֶ+2yֶ)ֶ в)(2aֶ+b)ֶ г)(4p-tֶ)ֶ Разложите на множители: а) аֶ-25 б)-0.16хֶ +yֶ в)(x+1)ֶ-4
Решение: 1. a) a² +(3a -b)²=a² +9a² - 6ab +b² =10a² -6ab +b²
b) (8x-y)² -64x² =64x² -16xy +y² -64x² =y² -16xy
в) 2(a -b)² =2(a² -2ab +b²) = 2a² -4ab +2b²
г) -y(3x -y)²= -y(9x² -6xy+y²) = -9x²y +6xy² -y^3
значок ^ обозначает в степени
2. a) =(x -3)(1 -y)
b) x -p +(p -x)c =x -p -(x -p)c =(x -p)(1 -c)
3. a) (c² -1)² =c^4 -2c² +1
b) (x² +2y²)² =x^4 +4x²y² + 4y^4
в) (2a²+b)²=4a^4 +4a²b +b²
г) (4p -t²)² =16p² -8pt² +t^4
4. a) a² -25 =(a -5)(a +5)
b) -0.16x² +y² =(-0.4x +y)(y + 0.4x)
в) (x +1)² -4 =(x+1 -2)(x+1 +2) =(x -1)(x +3)Выполнить алгебраические преобразования
а) с^3 - 3c
б) (32a^-8)^-3/4
Решение: $$ 1)c^3-3c=c(c^2-3)=c(c- \sqrt{3} )(c+ \sqrt{3} ) \\ 2)(2^5a ^{-8} ) ^{-3/4}=2 ^{-15/4} a^{6}=a^6/8 \sqrt[4]{8} $$