упрощение выражений »

выполните преобразование - страница 3

  • Решите неравенство: 3(x-2)-4(x+1)<2(x-3)-2 и обоснуйте все преобразования, которые будете при этом выполнять


    Решение: 3(x-2)-4(x+1)<2(x-3)-2
    Раскроем скобки и приведём подобные:
    3x-6-4x-4<2x-6-2
    -x-10<2x-8
    Перенесём все слагаемые с x в левую часть неравенства, все свободные члены в правую и приведём подобные:
    -x-2x<10-8
    -3x<2
    Разделим обе части неравенства на -3. Знак неравенства поменяется, т. к.3<0
    x>-2/3

  • Выполните преобразование дробных выражений


    Решение: $$ = \frac{a+b}{1}* \frac{b-a}{ab} * \frac{a^2b^2}{(a-b)(a+b)}=-ab \\ \\ =( \frac{ab}{(a-b)(a+b)} - \frac{b}{2(a-b)} )* \frac{(a-b)(a+b)}{2b} = \\ = \frac{2ab-b(a+b)}{2(a-b)(a+b)} * \frac{(a-b)(a+b)}{2b}= \\ =\frac{2ab-ab-b^2}{4b}= \frac{b(a-b)}{4b} = \frac{a-b}{4} $$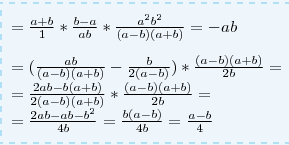

    frac a b frac b-a ab frac a b a-b a b -ab frac ab a-b a b - frac b a-b frac a-b a b b frac ab-b a b a-b a b frac a-b a b b frac ab-ab-b b frac b a-b b frac a-b...

  • Выполните преобразование по соответствующей формуле
    вот примеры: решите сколько сможете желательно сейчас
    (х+5)^2 = (2+у)^2 = (p+a)2 =
    (а-2)^2 = (6-с)^2 = (x-12)2 =
    (5а-2)^2 = (2х+9)^2 = (6y-1)^2 =
    (4х+у)^2 = (7m-3n)^2 = (-3x+a)^2 =
    (а^2-1)^2 = (b+c^3)^2 = (x^2-y^2)^2 =
    cам тему забыл, так что по 1 столбику выкладываете, благодарен заранее, очень надеюсь на вас.


    Решение: $$ (x+5)^2= x^{2} +10x+25 \\ (2+y)^2=4+4y+y^2 \\ (p+a)2=2p+2a $$ если задание написано не верно $$ (p+a)^2=p^2+2ap+a^2 \\ (a-2)^2=a^2-4a+4 \\ (6-c)^2=36-12c+c^2 \\ (x-12)2=2x-24 $$ или $$ (x-12)^2=x^2-24x+144 \\ (5a-2)^2=25a^2-20a+4 \\ (2x+9)^2 = 4x^2+36x+81 \\ (6y-1)^2 =36y^2-12y+1 \\ (4x+y)^2 =16x^2+8xy+y^2 \\ (7m-3n)^2=49m^2-42mn+9n^2 \\ (-3x+a)^2 =9x^2-6ax+a^2 \\ (a^2-1)^2 =a^4-2a^2+1 \\ (b+c^3)^2 = b^2+2bc^3+c^6 \\ (x^2-y^2)^2 =x^4-2x^2y^2+y^4 $$

  • Выполните преобразование по соответствующей формуле:
    (9+a)^2 (a+c)^2
    (8-b)^2 (11-y)^2
    (3y-4)^2 (10+4c)^2
    (5a+6b)^2 (-3c+a)^2
    (a-y^3)^2 (a^+b^2)^2


    Решение: 81+18а+а²
    а²+2ас+с²
    64-16в+в²
    121-22у+у²
    9у²-24у+16
    100+80с+16с²
    25а²+60ав+36в²
    а²-6ас+9с²
    а²-2ау³+у⁶
    а⁴+2а²в²+в⁴

    .

    а а а ас с - в в - у у у - у с с а ав в а - ас с а - ау у а а в в ....

  • Выполните преобразование:
    а) (8x^3-y^3/4x^2-y^2) * (y+2x/(2x-y)^2+6xy)
    б) (x-3/2x+4) * (x^2-4/x^3-27) * (x^2-3x+9/x^2-2x)


    Решение: А) Рассмотрим первый множитель:
    ((2x)³-y³)/((2x)²-y²)=(2x-y)(4x²+2xy+y²)/((2x-y)(2x+y)=(4x²+2xy+y²)/(2x+y).
    Рассмотрим второй множитель:
    (y+2x)/((2x-y)²+6xy)=(2x+y)/(4x²-4xy+y²+6xy)=(2x+y)/(4x²+2xy+y²).
    Умножаем первый множитель на второй и получаем: 1.
    б) Первый множитель:
    (x-3)/(2(x+2))
    Второй множитель:
    (x-2)(x+2)/((x-3)(x₂+3x+9))
    Третий множитель:
    (x²+3x+9)/(x(x-2)).
    Умножаем второй множитель на третий и получаем: (x+2)/(x(x-3)).
    Умножаем полученное произведение на первый множитель и получаем: 1/(2x).

<< < 123 4 > >>