неравенства »

решите неравенство - страница 2

  • Иррациональное неравенство sqrt(3x - 2) =< -2

    =< (меньше или равно)


    Решение: Квадратный корень из любого числа больше либо равен нулю. Так как -2<0, то указанное неравенство не имеет решений.
    Ответ: нет решений

    $$ \sqrt{3x-2} \leq -2 $$

    По определению квадратного корня мы знаем ,что он имеет смысл если подкоренное больше или равно нулю и принимает только неотрицательные значения , поэтому данное уравнение не имеет корней
    Ответ : нет корней

  • Решите неравенство х^2 +6x +5 >0 методом параболы


    Решение: Берете значение например 0 это будет х на графике и подставляете его в свое уравнение и получится 5 , отмечаете эту точку(0;5) и так далее пока не получится парабола . Если не так, то можно с помощью дискриминанта Д=36-20=16
    Х1=-6-4/2=-10/2=-5
    Х2=-6+4/2=-2/2=-1
    Отметить эти точки а потом сделать симметрию...

  • Решение неравенство х^2+5х-14 больше или равно методом параболы


    Решение: Ветки параболы направлены вверх. Поэтому нам нужны значения, которые выше оси $$ (x) $$.

    1. Найдём нули функции:
    $$ x^2+5x-14=0 \\ D=25+14*4=25+56=81 \\ x_1=(-5+9):2=4:2=2\\x_2=-14:2=-7. $$

    Теперь делаем такую таблицу () и по ней чертим график — надеюсь, понятно, как это сделать. И теперь заштриховываем на графике ту область, которая выше оси $$ x $$, то есть промежуток: $$ (-\infty; -8) \cup (2; + \infty). $$.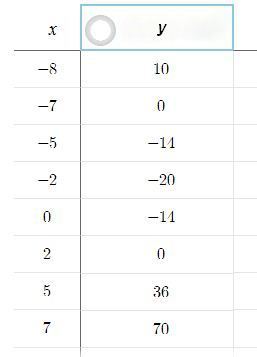Ветки параболы направлены вверх. Поэтому нам нужны значения которые выше оси x . . Найд м нули функции x x- D x - x - - . Теперь делаем такую таблицу и по ней чертим график...

  • Решить неравенство методом парабол: $$ \frac{x^2 - 3x}{6} - \frac{x + 1}{9} > \frac{x - 14}{18} $$


    Решение: Всё просто - правую часть неравенства переносите в левую часть (меняя знак на противоположный), далее приводите к обычному квадратному уравнению (ax2+bx+c=0), это и будет функция у от х. y(x)=(ax2+bx+c=0)
    Всем известно, что графиком квадратичной функции является парабола.
    Находите х - это будут точки пересечения с осью Х.
    Теперь надо выяснить направление ветвей.
    Если а>0     то ветви параболы направлены вверх, если a<0, то вниз.
    Решением будут абсциссы (координаты х) точек графика, ординаты (координаты у) которых больше нуля, т.е. лежат в верхней полуплоскости.

  • Показательное неравенство. $$ 2^{x + 3} + 4^x - 9 < 0 $$


    Решение: Приравниваем неравенство к нулю
    $$ x^{x+3}+4^x-9=0 $$

    Путем подбора находим решение
    $$ x=0 $$

    Других решений нет, так как функция, соответствующая данному уравнению, является монотонной.
    На промежутке отмечаем
    _____    (-)_____(0)______+______>

    Ответ:     $$ x \in (-\infty;0). $$

<< < 12 3 4 > >>