сумма степеней - страница 8
найдите сумму многочленов 2х(х в 3 степени)-2х и -х(во 2 степени)+2х-1
Решение: 2х³-2х+х²+2х-1=2х³+х²-1если стоит минус во втором многочлене перед х², тогда будет так
2х³-2х-х²+2х-1=2х³-х²-1
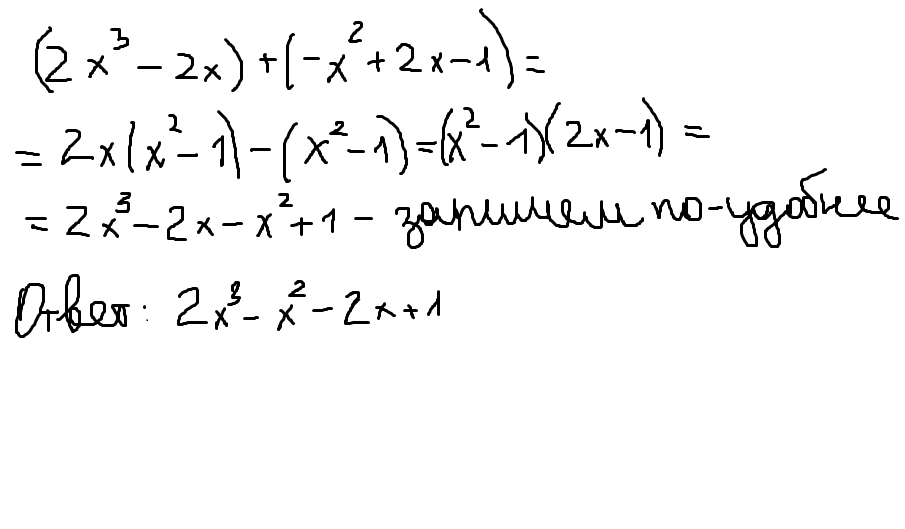
Представьте дробь в виде суммы двух дробей, знаменатель которых - многочлены первой степени относительно X х+28 - х в квадрате- 36 3х- 4 - х в квадрате+ 10х+24
Решение: Воспользуемся методом неопределенных коэффициентовА В А * (Х + 6) + В * (Х - 6) (А + В) * Х + (6 * А - 6 * В) Х + 28
- + - = - = - = -
Х - 6 Х + 6 (Х - 6) * (Х + 6) Х² - 36 Х² - 36
Приравнивая коэффициенты при подобных членах получаем систему линейных уравнений
А + В = 1 А = 17/6
6 * А - 6 * В = 28, откуда B = -11/6
Таким образом
Х + 28 17/6 11/6
- = -
Х² - 36 Х - 6 Х + 6
Представьте дробь в виде суммы двух дробей, знаменатели которых-многочлены первой степени относительно x :
а)\( \frac{5x-1}{x(x-1)} \)
б)\( \frac{7x-6}{(x+2)(x-3)} \)
Быстрее
Задание 8 класса
Решение: Воспользуемся методом неопределенных коэффициентова) 5 * Х - 1 А В А * (Х - 1) + В * Х (А + В) * Х - А
- = - + - = - = -
Х * (Х - 1) Х Х - 1 Х * (Х - 1) Х * (Х - 1)
Приравнивая коэффициенты при степенях Х, получаем систему уравнений
А + В = 5 А = 1
- А = -1, откуда В = 4
Итак
5 * Х - 1 4 1
- = - + -
Х * (Х - 1) Х - 1 Х
б) 7 * Х - 6 А В А*(Х - 3) + В*(Х + 2) (А + В)*Х + (-3*А + 2*В)
- = - + - = - = -
(Х + 2)*(Х - 3) Х + 2 Х - 3 (Х + 2) * (Х - 3) (Х + 2) * (Х - 3)
Приравнивая коэффициенты при степенях Х, получаем систему уравнений
А + В = 7 А = 4
- 3 * А + 2 * В = -6, откуда В = 3
Итак
7 * Х - 6 4 3
- = - + -
(Х + 2) * (Х - 3) Х + 2 Х - 3
Представьте дробь в виде суммы двух дробей, знаменатели которых - многочлены первой степени : x+28/x^2-36
Решение: Метод неопределённых коэффициентов.
(x+28)/[(x-6)(x+6)]=A/(x-6)+B/(x+6)
Складываем дроби
[A(x+6)+B(x-6)]/[(x-6)(x+6)]=
[x(A+B)+(6A-6B)]/(x^2-36)
Дроби равны, знаменатели равны, значит, числители тоже одинаковы.
x(A+B) + 6(A-B) = x+28
Коэффициенты при одинаковых степенях должны быть равны.
A+B=1
A-B=28/6=14/3
Складываем уравнения
2A=1+14/3=17/3; A=17/6; B=1-A=-11/6
(x+28)/(x^2-36)=-11/(6(x-6))+17/(6(x+6))Во сколько раз степень многочлена 4a^6- 2a^4 + a - 1 больше суммы его коэффициетнов ?))
Решение: Степень многочлена - высшая степень его одночленов, то есть у вас многочлен 6 степениСумма коэффициентов = 4+0-2+0+0+1-1=2
6:2=3
Ответ: в 3 раза
можно переписать:
4a^6-2a^4+1a-1*a^0
их сумма 4+(-2)+1+(-1)=2
степень многочлена - наивысшая его степень. у нас это 6
найдем во сколько раз степень больше суммы коэф:
6:2=3 раза