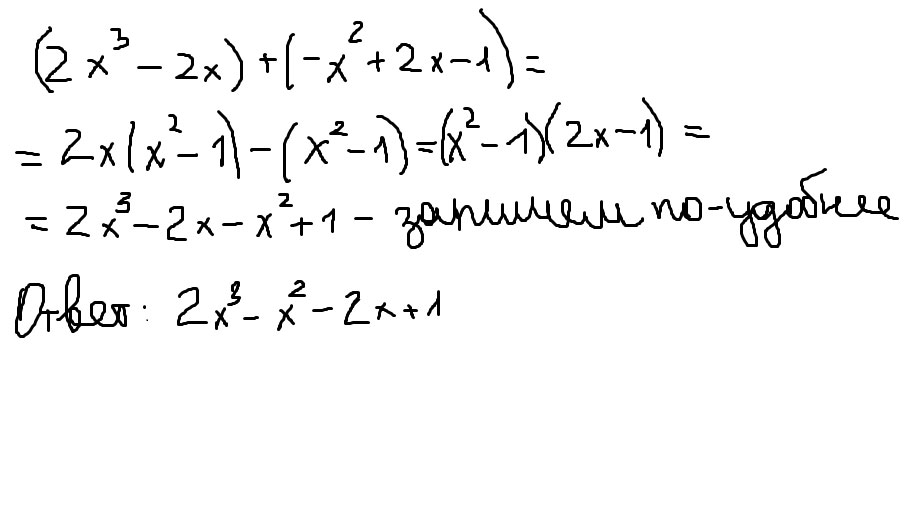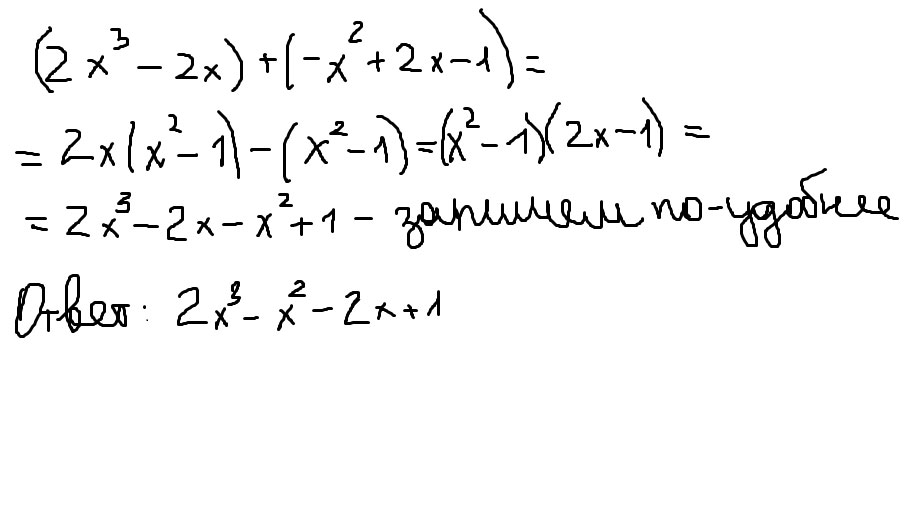степени »

сумма степеней - страница 6

  • 1) Вычислите \( \frac{2 ^{2k-1}*3 ^{2k-2} }{10*6 ^{2k-3} } \)
    2) Найдите значение выражения:\( \frac{28 ^{6} }{(4 ^{ \frac{5}{12} }*7 ^{ \frac{1}{2}) ^{12} } } \)
    3) Представьте выражение в виде суммы: \( m ^{ \frac{2}{3} }n(m ^{ \frac{1}{3}} +n ^{ \frac{1}{3} } ) \)
    4) Вычислите:
    \( \frac{1}{1- \frac{1}{1-2 ^{-1} } } + \frac{1}{1+ \frac{1}{1+2 ^{-1} } } \)
    5) Расположите в порядке возрастания числа \( 2 \sqrt{33} ; 3 \sqrt{14} и 8 \sqrt{2} \)
    6) Найдите значение выражения: \( \frac{ \sqrt{n}-1.1 }{ \sqrt{k} }, \) ,где n=0.49, k=0.64

    7) Записать выражение \( (c ^{9} ) ^{15} * c ^{3} \) в виде степени с основанием c.
    8) Вычислить:\( \sqrt{4- \sqrt{7} } - \sqrt{4+ \sqrt{7} } \)


    Решение: 7) 9+15+3=с^27
    6) $$ \frac{ \sqrt{0.49}-1.1 }{\sqrt{0.64}}= \frac{0.7-1.1}{0.8}=-0.5 $$
    3) раскрываем скобки и получаем $$ mn+m^ {\frac{2}{3}}n \frac{4}{3} $$
    5)$$ 2 \sqrt{33}= \sqrt{132} \\ 3 \sqrt{14}= \sqrt{126} \\ 8 \sqrt{2}= \sqrt{128} $$
    Ответ: $$ 1)3 \sqrt{14} \\ 2)8 \sqrt{2} \\ 3)2 \sqrt{33} $$
    4) решаем снизу верх $$ 2^-1=0.5 \\ 1-0.5=0.5 \\ \frac{1}{0.5}=2 \\ 1-2=-1 \\ \frac{1}{-1}=-1 $$
    это получилось в левой части 
    $$ 2^{-1}=0,5 \\ 1+0.5=1.5 \\ \frac{1}{1.5}= \frac{2}{3} \\ 1+ \frac{2}{3}= \frac{5}{3} \\ \frac{1}{ \frac{5}{3} }= \frac{3}{5} $$
    теперь сумма
    $$ -1+ \frac{3}{5}=- \frac{2}{5} $$
    Ответ $$ \frac{2}{5} $$

  • Некоторое число а возвели в третью степень. полученное трехзначное число записали в обратном порядке,получили простое число.Найдите исходное число а. В ответе укажите сумму цифр а^4.


    Решение:

    Число, куб которого получается трехзначным числом, должно быть меньше 10, т.к. 10³=1000 - четырехзначное число, все последующие - тем более не подходят. 

    4³=64 

    5³=125

    Записав это число в обратном порядке, получим 521. Это - простое число ( смотри таблицу простых чисел)

    5⁴=625

    Сумма цифр этого числа 6+2+5=13

  • Передставьте целое выражение в виде прозведения многочлена г)5a+5b-ax-bx e)m (во второй степени )-mn-2n+2m з)x (во четвёртой степени)-3x(в третей степени)+3x(во второй степени)-9x разложите мночлен на множители,предварительно представив один из его членов в виде суммы д) m(во второй степени)-3mn+2n(во второй степени)


    Решение:

    г)5a+5b-ax-bx = 5(а+b)-x(a+b) = (a+b)(5-x)

    e)m²-mn-2n+2m = m(m+2)-n(m+2) = (m+2)(m-n)

    з)x4-3x³+3x²-9x = x³(x-3)+3x(x-3) = (x-3)(x³+3x) = x(x²+3)(x-3)

    д) m²-3mn+2n² = m²-mn-2mn+2n² =\\= m(m-n)-2n(m-n) = (m-n)(m-2n) 

    г)$$ 5a+5b-ax-bx=5(a+b)-x(a+b)=(a+b)(5-x) $$

    e)$$ m^{2}-mn-2n+2m=(m^{2}+2m)+(-mn-2n)=\\=m(m+2)-n(m+2) = (m+2)(m-n) $$

    з)$$ x^{4}-3x^{3}+3x^{2}-9x=x^{3}(x-3)+3x(x-3)=\\=(x-3)(x^{3}+3x) = x(x^{2}+3)(x-3) $$

    д)$$ m^{2}-3mn+2n^{2}=m^{2}+(-mn-2mn)+2n^{2}=\\= (m^{2}-mn)+(-2mn+2n^{2})=(m^{2}-mn)-(2mn-2n^{2})=\\=m(m-n)-2n(m-n)=(m-n)(m-2n) $$

  • Во сколько раз степень многочлена 4a^6- 2a^4 + a - 1 больше суммы его коэффициетнов??))


    Решение: Степень многочлена - высшая степень его одночленов, то есть у вас многочлен 6 степени

    Сумма коэффициентов = 4+0-2+0+0+1-1=2

    6:2=3

    Ответ: в 3 раза

    можно переписать:

    4a^6-2a^4+1a-1*a^0

    их сумма 4+(-2)+1+(-1)=2

    степень многочлена - наивысшая его степень. у нас это 6

    найдем во сколько раз степень больше суммы коэф:

    6:2=3 раза

  • Найдите сумму многочленов 2х(х в 3 степени)-2х и -х(во 2 степени)+2х-1


    Решение: 2х³-2х+х²+2х-1=2х³+х²-1

    если стоит минус во втором многочлене перед х², тогда будет так

    2х³-2х-х²+2х-1=2х³-х²-1

    х - х х х- х х - если стоит минус во втором многочлене перед х тогда будет так х - х-х х- х -х -...
<< < 456 7 8 > >>