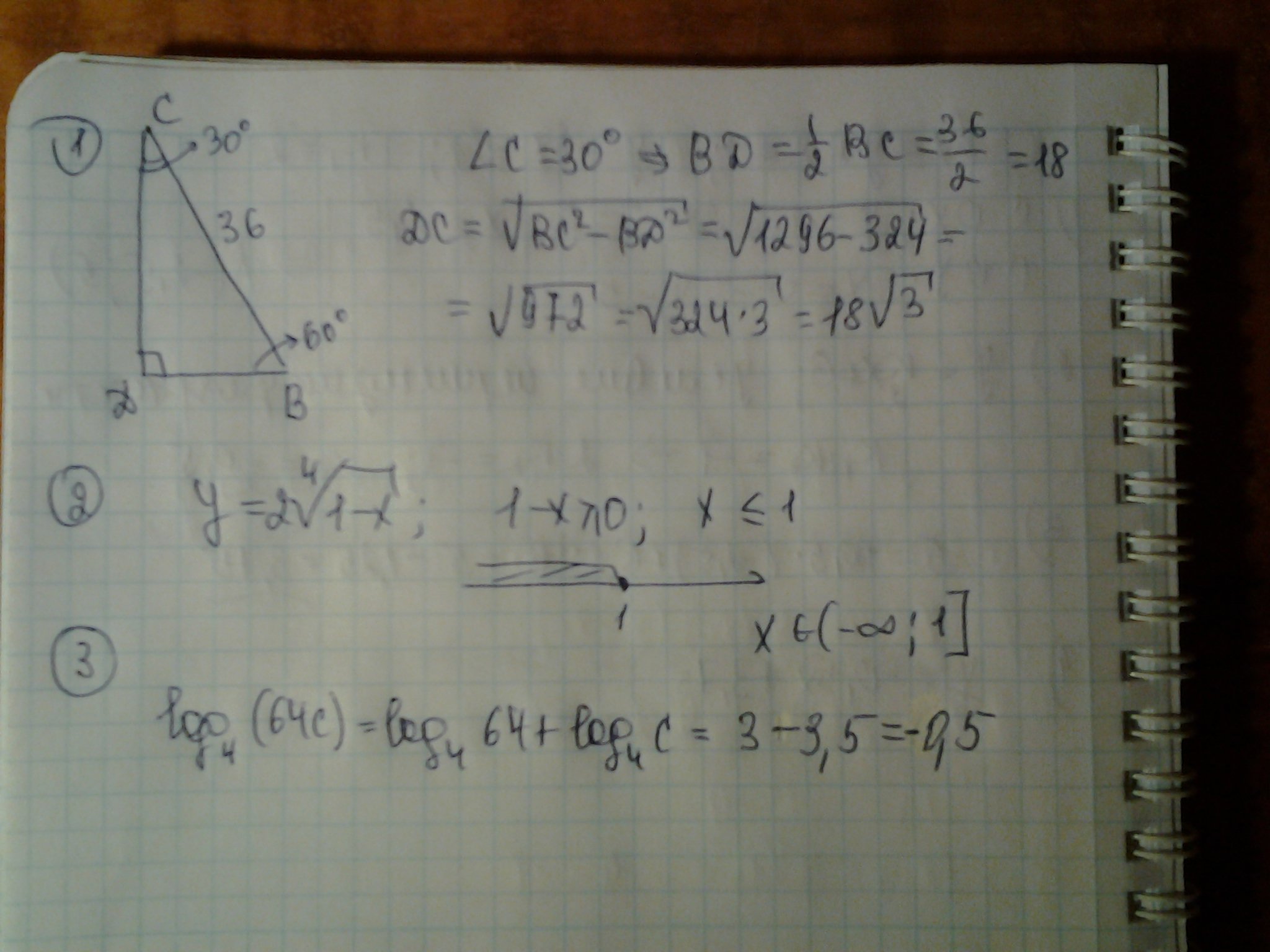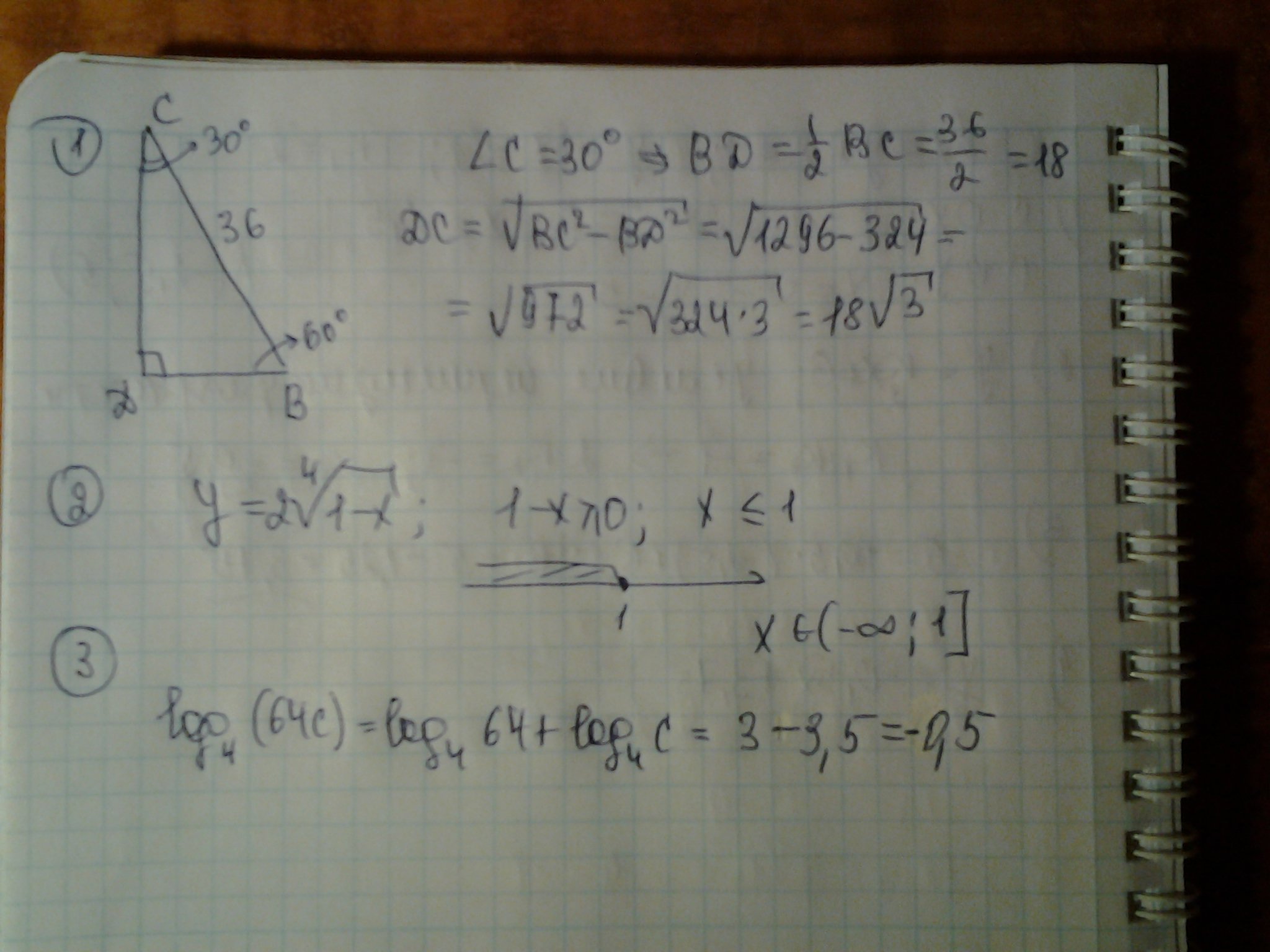степени »
степень логарифма - страница 5
Как решать \( 7^{4log_73} \)?
Решение: $$ 7^{4log_73} $$
Здесь банальные свойства логарифмов. Надо делать постепенно. Сначала смотрим на сам логарифм:
$$ 4log_73 $$
Надо преобразовать логарифм. По свойству:
$$ m \log_ab=log_ab^m $$
$$ 4log_73=log_73^4=log_781 $$
Далее решаем весь пример:
$$ 7^{log_781} $$
Снова свойство логарифма:
$$ a^{log_ab}=b $$
$$ 7^{log_781}=81 $$
Ответ: 81Решить логарифм: ( корень из 7) в степени 2 / log 7 по основанию 125
Решение: Основное логарифмическое тождество
$$ a^{log_ab}=b, \\ a > 0,a eq 1,b > 0 $$
Из формулы перехода к другому основанию
$$ log_ab= \frac{1}{log_ba}, \\ a > 0,a eq 1,b > ,b eq 1 $$
$$ (\sqrt{7})^{ \frac{2}{log_{125}7}}= ( \sqrt{7})^{ 2\cdot log_{7}125}=(7^{ \frac{1}{2}})^{ 2\cdot log_{7}125} =7^{ log_{7}125}=125 $$
1 задание. корень кубический, под ним корень четвертый из а в 6 степени, если а больше или равно 0. 2 задание.если логарифм с числом 3 и основой4 = а, то логарифм с числом 9 и основой 16= решите
Решение:1) извлечение корня --- возведение в дробную степень
при возведении в степень --- показатели степеней перемножаются
... = a^(6 * 1/4 * 1/3) = a^(1/2) = корень(a)
2) log 4 (3) = a
log 16 (9) = log 4^2 (3^2) = 1/2 * log 4 (3^2) = 1/2 * 2 * log 4 (3) = a
формулы: log a^n (b) = 1/n * log a (b) log a (b^n) = n * log a (b)
На доске записано шесть натуральных чисел, таких, что для любых двух a и b из них, logab или logba – целое число (второй логарифм при этом не обязансущестовать). Какое наименьшее значение может принимать максимальное из этих чисел? Ответ можно записать в виде степени числа: mn обозначается как m^n.
Решение: Вообще, если я правильно понимаю, то такое возможно в случае, если все эти числа будут совпадать(возможно за исключением одного), т.е. набор 1 2 2 2 2 2 будет подходить под эту систему. ( У нас ведь не сказано, что числа различные?). В ином случае, это возможно, только если каждое последующее число будет квадратом следующего. Начнем опять с 1, т.е. получаем 1, 2, 2^2, 2^4, 2^8, 2^16 (по идее, меньше не может быть)1. В прямоугольном треугольнике ВСД угол Д=90* гипотенуза ВС=36 угол СВД=60. Найти длину катета.
2. Областью определения функции у=2 умножить на корень 4 степени под корнем 1-х, является множество .........
2. Вычислить логарифм: лог4. 64с, если лог4. с=-3,5
Решение: Применены : свойство катета против угла в 30 градусов, теорема Пифагора, область определения корня чётной степени, свойства логарифмов