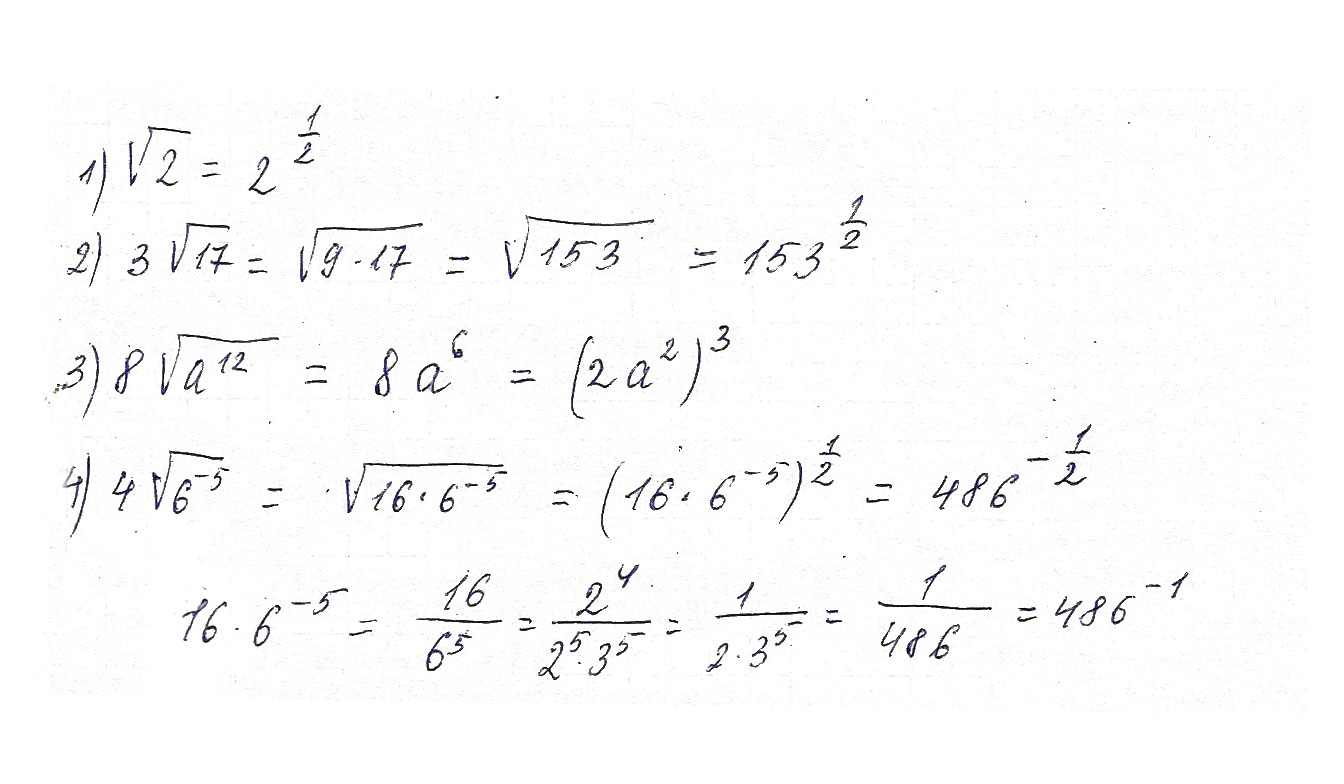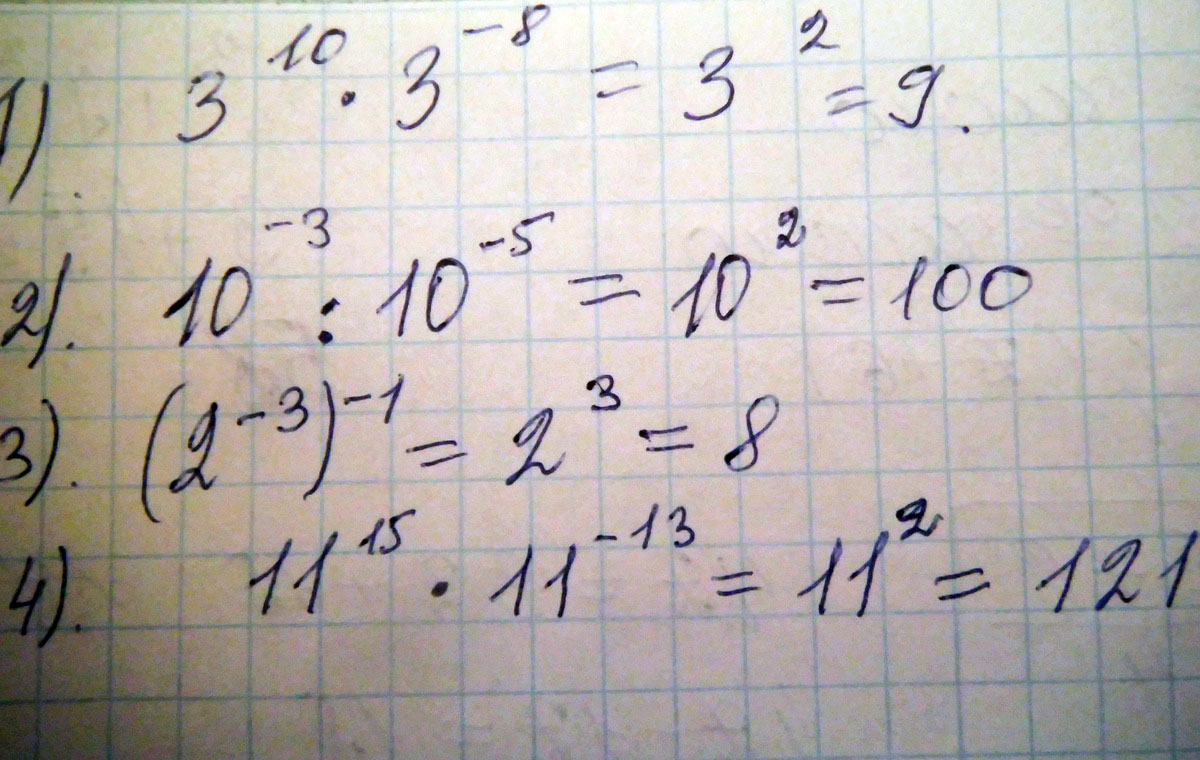степени »

представьте выражение в виде степени с основанием

  • Представьте выражение в виде степени с рациональным показателем корень из 2, 3корня из 17, 8 корней из а в 12ой степени, 4 корня из 6 в -5 степени?


    Решение: Решение на рисунке

    1) V 2 = 2 ^ 1\2 (два в степени 1\2)

    2) 3 V 17 = V 9 * 17 = V 153 = 153 ^ 1\2

    3) 8 V A ^ 12 = 8 * A ^ 6 = 2 ^ 3 * A ^6 = (2A^2)^3

    4) (4 V 6 ) ^-5 = (V 6 * 16 )^-5 = (V 2*3 * 2^4 )^-5 = (V 3* 2^5)^-5 = (1\3)^5 * (2)^-25

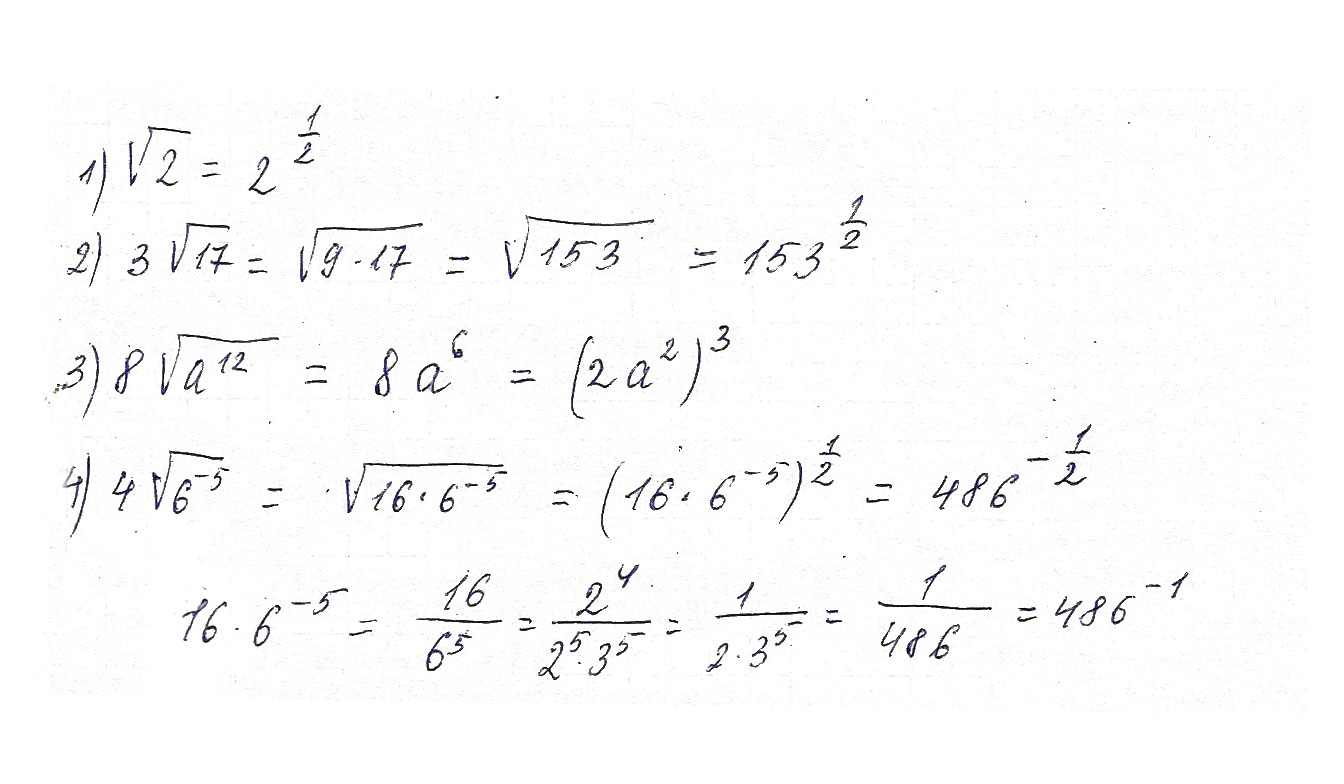
    Решение на рисунке V два в степени V V V V A A A A V - V - V - V - -...

  • Представьте в виде степени выраженияа)7 в 6 степени умножить 343
    б)216 умножить (-6) в 4 степени
    в)729 умножить 27
    г)625 умножить (-25)
    д)3 в степени n+5 умножить 81
    е)216 умножить 6 в степени n+2


    Решение: А) =7 в 6 степени * 7 в 3 степени = 7 в 9 степени
    Б) =6 в 3 степени * 6 в 4 степени = 6 в 7 степени
    В) =9 в 3 степени * 3 в 3 степень = 3 в 6 степени * на 3 в 3 степени = 3 в 9 степени
    Г) =5 в 4 степени * -5 во 2 степени = -5 в 6 степени
    Д) =3 в степени n+5 * 3 в 4 степени = 3 в степени n+9
    Е) =6 в 3 степени * 6 в степени n+2 = 6 в степени n+5

  • Представьте в виде степени и найдите значение выражения. 1) 3 в 10 степени умножить на 3 в минус 8 степени. 2) 10 минус 3 степени разделить 10 минус 5 степени. 3) (2 минус 3 степени)минус 1 степени .4) 11 в 15 степени умножить 11 минус 13 степени.


    Решение: Степени с одинаковыми основаниями при делении вычитаются, а степени с одинаковыми основаниями при умножении складываются. Решение на фото. Степени с одинаковыми основаниями при делении вычитаются а степени с одинаковыми основаниями при умножении складываются. Решение на фото....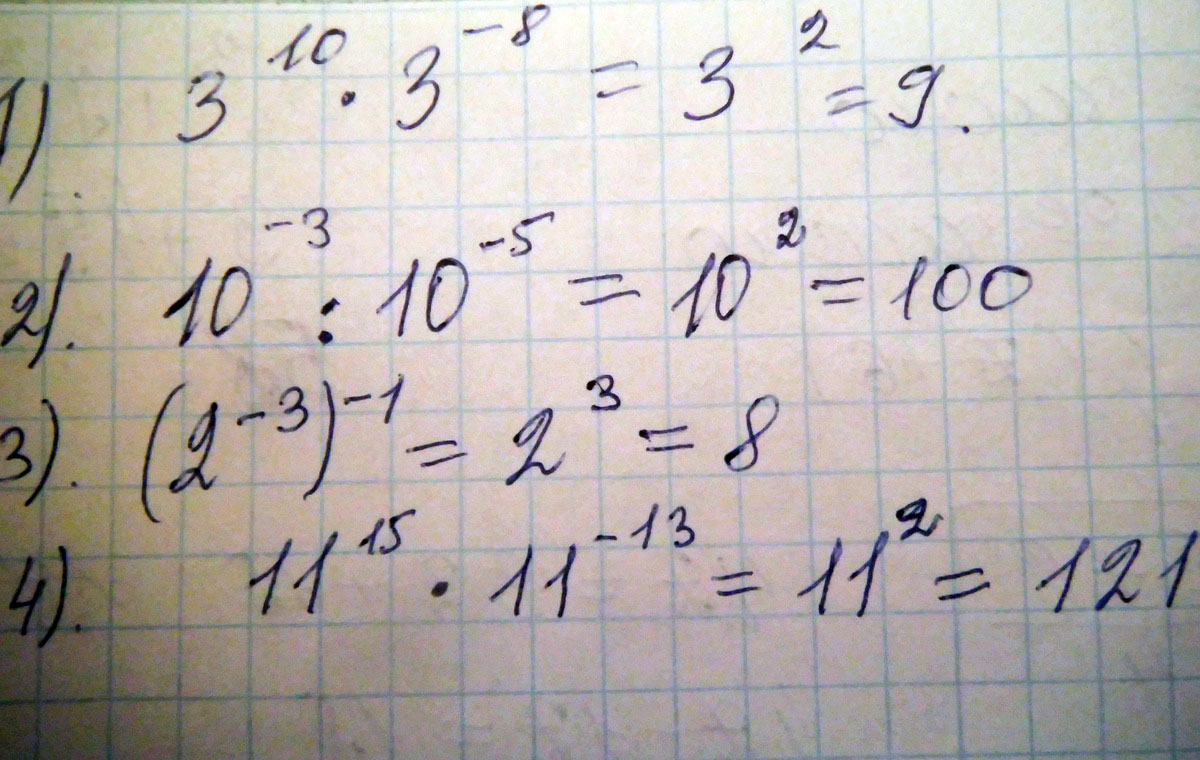

  • Представьте выражение (А в 4 степени)-во 2 степени _____________ А в -7 степпени в виде степени с основанием a.В ответе укажите эту степень.


    Решение: А в 8 степени деленая на а -7 = А в первой или просто А

    (a в 4степени ) во 2 степени :а в 7 степени =а в степени(4*2): а в 7 спепени

    а в степени (8-7)=а в первой степени
     при деление степени с одинаковым основанием вычитаются

    а когд степень в степен, они умножаются, поэтому (4*2)

  • Представьте выражения в виде произведения степеней: (3b) в 5 степени (-5q) в 4 степени (ab) d 4 степени (-am) в 8 степени (a во 2 степени*b*c в 3 степени) в 4 степени (6a в 5 степени *b*x в 3 степени) в 4 степени


    Решение:

    по формулам поднесения степеня произведения к степеню

    (3b) в 5 степени=3^5 * b^5

    (-5q) в 4 степени=(-1)^4*5^4 *q^4=5^4 *q^4

    (ab) в 4 степени= a^4 *b^4

    (-am) в 8 степени=(-1)^8 *a^8 *m^8=a^8 *m^8

    (a во 2 степени*b*c в 3 степени) в 4 степени =(a^2)^4 *b^4 * (c^3)^4=

    =a^(2*4) * b^4 8 c^(3*4)=a^8 * b^4 * c^12

    ( (6a) в 5 степени *b*x в 3 степени) в 4 степени=(6^5)^4 *(a^5)^4*b^4*(x^3)^12=

    =6^20* a^20 * b^4 *x^12

    ( 6a в 5 степени *b*x в 3 степени) в 4 степени=6^4 *(a^5)^4*b^4*(x^3)^12=

    =6^4* a^20 * b^4 *x^12

1 2 3 > >>